АВСD со стороной а и углом ВАD =
60°. Плоскость ВС1D составляет с плоскостью основания угол равный 60° Найти площадь боковой поверхности параллелепипеда.∠
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть






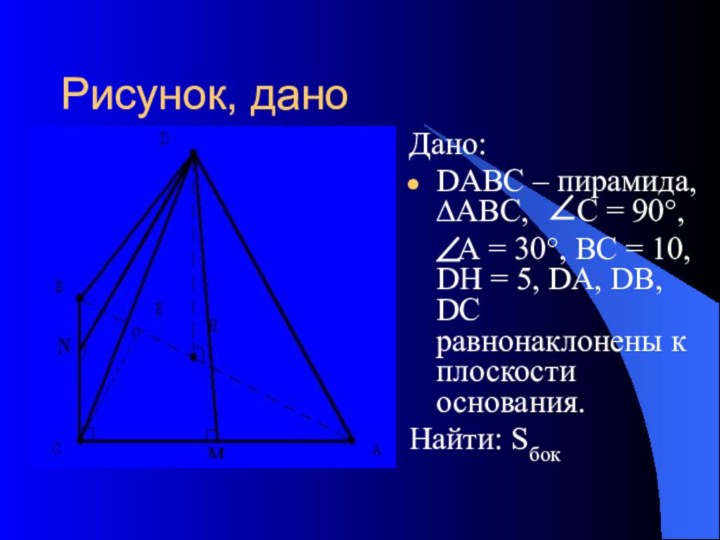





∠
∠
∠
∠
∠
∠
∠
∠
∠
∠
∠
∠
∠
∠
∠
∠
∠
∠
∠
∠
∠
∠