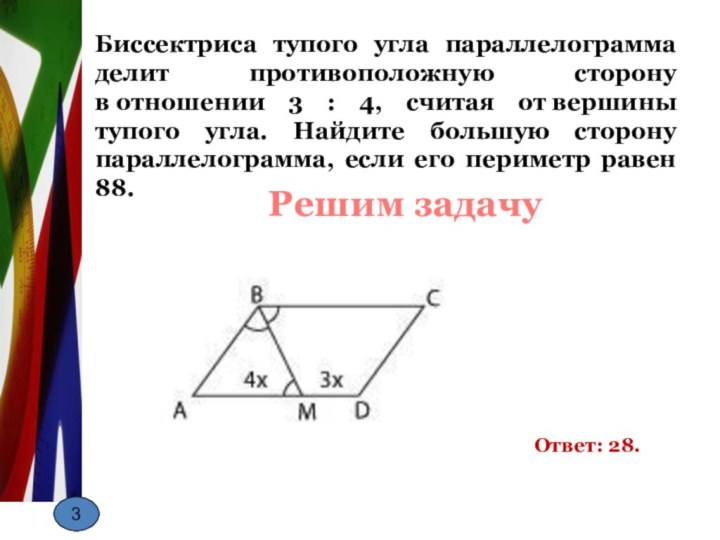
3 : 4, считая от вершины тупого угла. Найдите большую
сторону параллелограмма, если его периметр равен 88.Ответ: 28.
Решим задачу
3
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть






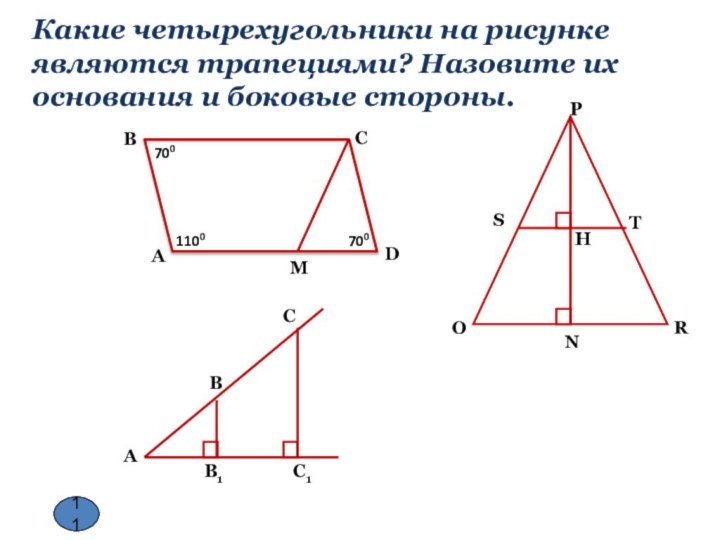


















Ответ: 28.
Решим задачу
3
9
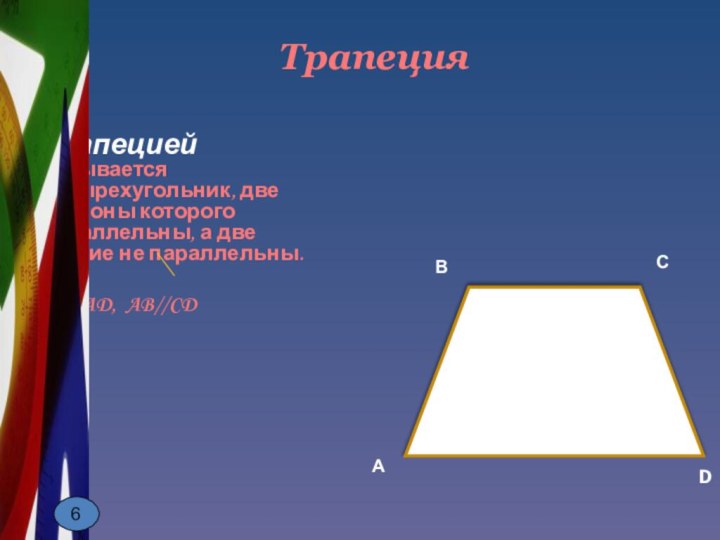
Столовая гора –
гора с усечённой, плоской вершиной.
Город Трапезунд
10
13
14
А
В
С
D
А
В
С
D
M
N
15
А
В
С
D
22
А
В
С
D
23
А
В
С
D
25
27
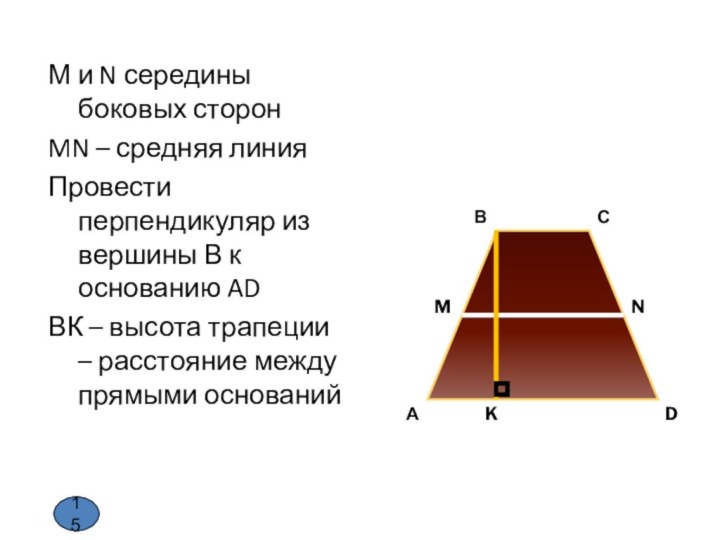
15
28