Презентация на тему Геометрические построения 6 класс

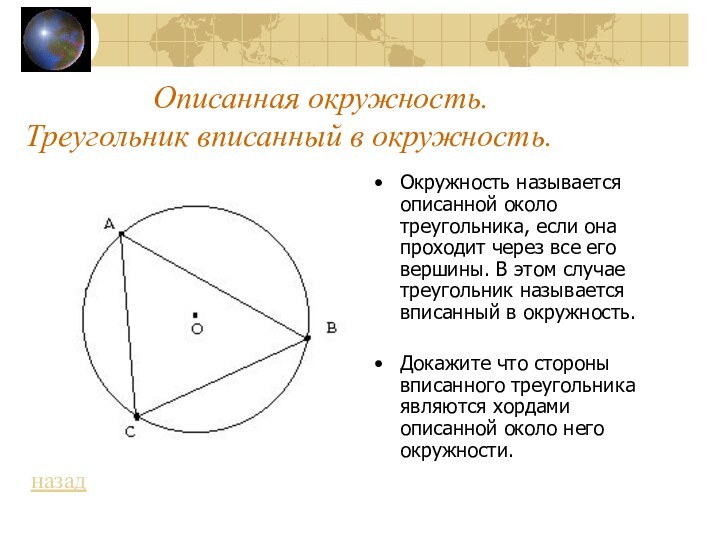
Описанная окружность.Треугольник вписанный в окружность.
6 6 Серединный перпендикуляр6 Серединный

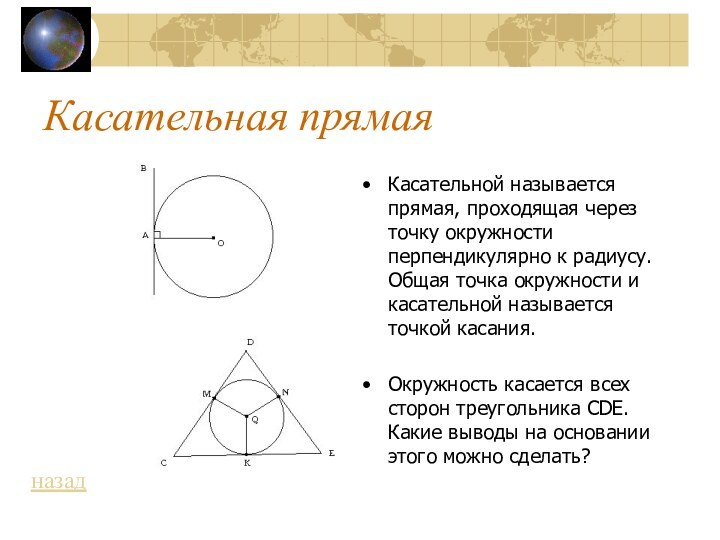
перпендикуляр.
7 7 Касательная прямая7 Касательная прямая.
8 8 Окружность вписанная в треугольник8 Окружность вписанная в треугольник.
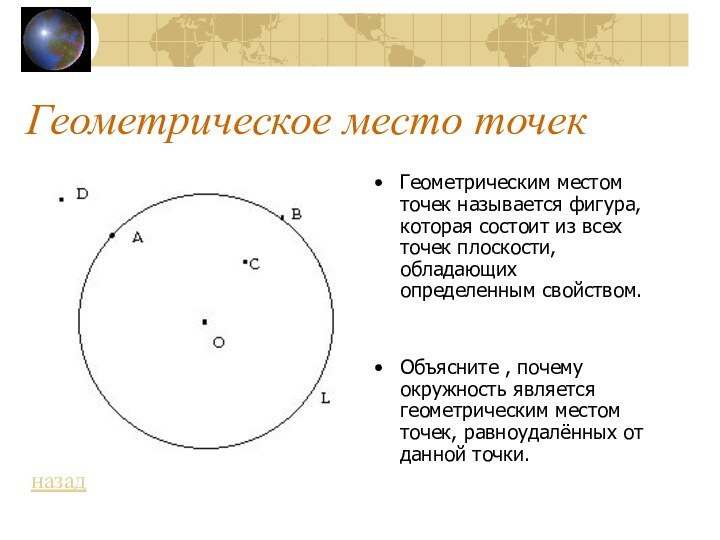
9 9 Геометрическое место точек9 Геометрическое место точек.
10 10 Теорема о геометрическом месте точек10 Теорема о геометрическом месте точек.
11 11 Вписанный угол11 Вписанный угол.
12 Задача.
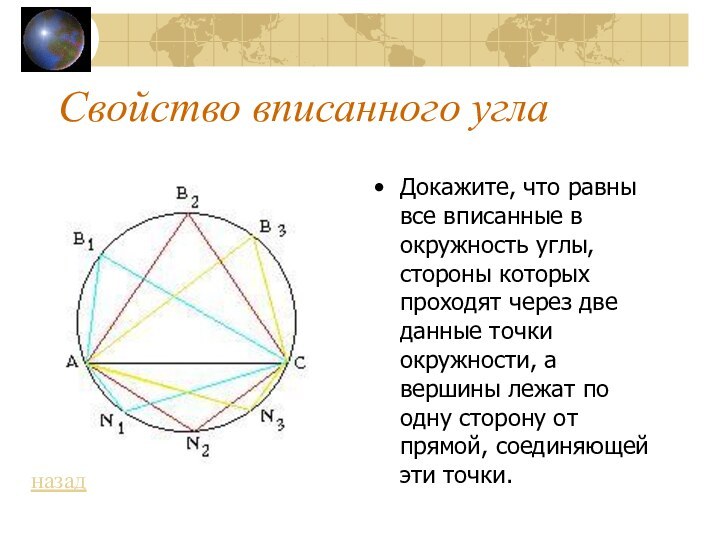
11313 13 Свойство вписанного угла13 Свойство вписанного угла.

точек плоскости, равноудалённых от данной точки – центра окружности.
Расстояние

от центра О окружности до лежащей на ней точки А равно 5 см. Докажите что расстояние от точки О до точки В этой окружности равно 5 см , а расстояние от О до точек С и D , не лежащих на ней не равно 5 см.

Окружность

назад

окружности и отрезок, соединяющий центр с любой точкой окружности.
Точки

X,Y,Z лежат на окружности T с центром М. .Является ли радиусом этой окружности
Отрезок MX;
Расстояние от точки М до точки Y;
Отрезок XZ ?

назад

Диаметр
Диаметром называется хорда, проходящая через центр.

Докажите что АВ диаметр.
Докажите

что диаметр равен двум радиусам.

назад

Описанная окружность.Треугольник вписанный в окружность.
Окружность называется описанной около треугольника,

если она проходит через все его вершины. В этом случае треугольник называется вписанный в окружность.

Докажите что стороны вписанного треугольника являются хордами описанной около него окружности.

назад

проходящая через середину отрезка АВ перпендикулярно к нему.


Докажите ,

что центр окружности лежит на серединном перпендикуляре к любой хорде этой окружности.

назад

перпендикулярно к радиусу. Общая точка окружности и касательной называется

точкой касания.

Окружность касается всех сторон треугольника CDE. Какие выводы на основании этого можно сделать?

назад

Окружность вписанная в треугольник
Окружность называется вписанной в

треугольник , если она касается всех его сторон. В этом случае треугольник называется описанный около окружности.

Треугольник ABC-описанный около окружности. Какие из треугольников AOM, MOB, BON, NOC, COK, KOA-равные?

назад

состоит из всех точек плоскости, обладающих определенным свойством.


Объясните ,

почему окружность является геометрическим местом точек, равноудалённых от данной точки.

назад

точек, равноудалённых от двух данных точек, есть прямая ,

перпендикулярная к отрезку, соединяющему эти точки, и проходящая через его середину.
Дано: а AB;AO=OB. Доказать: а- геометрическое место точек, равноудалённых от А и В.
Будет ли теорема доказана, если установить, что любая точка прямой а равноудалена от А и В.

назад

угол
Угол, вершина которого лежит на окружности, а стороны пересекают

эту окружность, называется вписанным в окружность.
Какие из углов являются вписанными в окружность?

назад

сторонами угла ABC.




Докажите, что угол ABC- прямой.

Задача

назад