- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку геометрии в 10 классе по теме Расстояние между точками
Содержание
- 2. Цель обучения10.4.2 уметь находить расстояние между двумя точками в пространстве
- 3. Критерии успеха: записывает формулу расстояния между
- 4. Повторение:1. Даны точки А ( - 1;
- 5. Повторение:2. Запишите координаты вектора Ненулевые векторы наз.
- 6. Повторение:4. Найдите координаты вектора
- 7. Задание прямоугольной системы координат в пространстве:ОyОy
- 8. Нахождение координат точек. Точка лежитна осиОу (0;
- 9. Решение задач.Рассмотрим точку А (2; -3; 5)хуz025-3A1)
- 10. Решение задач.хуzC1 - ?C - ?A1 (1;0;0)B1
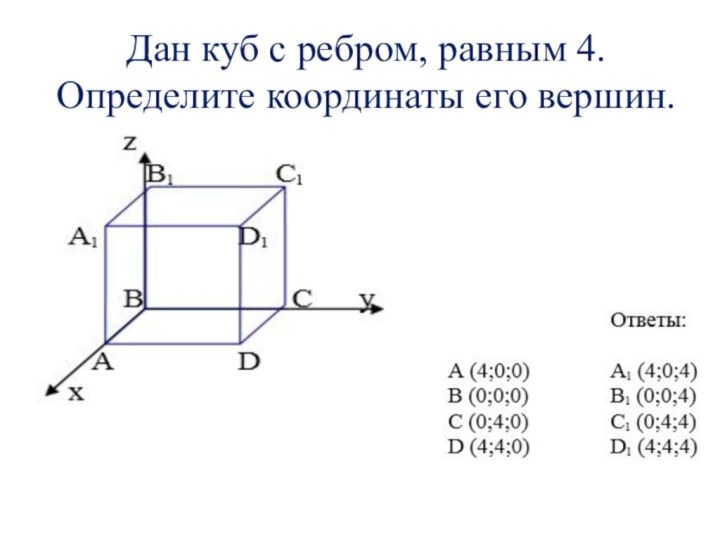
- 11. Дан куб с ребром, равным 4. Определите координаты его вершин.
- 12. Найти координаты точек А, В, С и
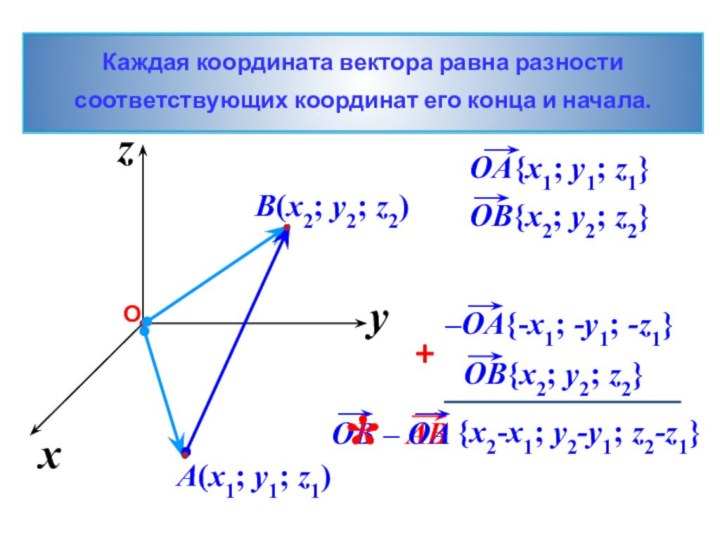
- 13. xzy{x2-x1; y2-y1; z2-z1}Каждая координата вектора равна разности соответствующих координат его конца и начала.*
- 14. BA(3;5;7),(5;4;-1),PC(2;-1;0),(4;-4;2),D(-3;-4;0),RT(-4;0;-4),(0;5;-1),N(3;2;-3),B(5;4;-1)A(3;5;7)C(4;-4;2)P(2;-1;0)T(0; 5;-1)R(-4;0;-4)O(0;0;0),O(0;0;0),ABON
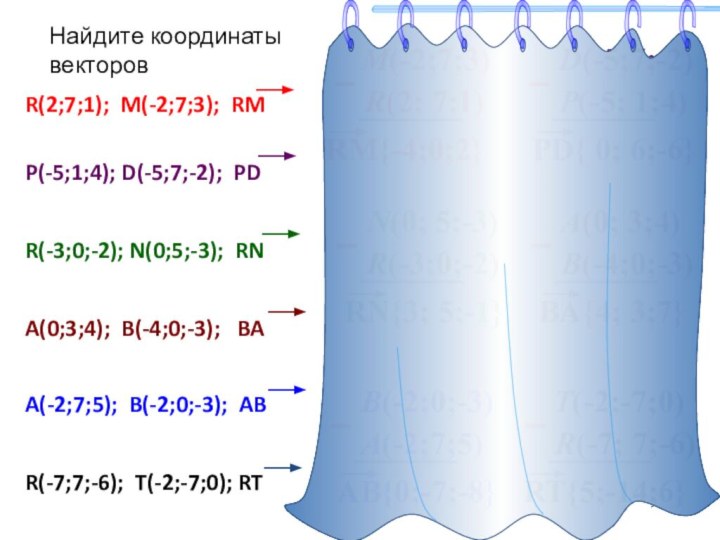
- 15. Найдите координаты векторовR(2; 7;1)M(-2;7;3)R(2;7;1); M(-2;7;3); RMP(-5;1;4); D(-5;7;-2);
- 16. xzyВычисление длины вектора по его координатамOA2= OA12
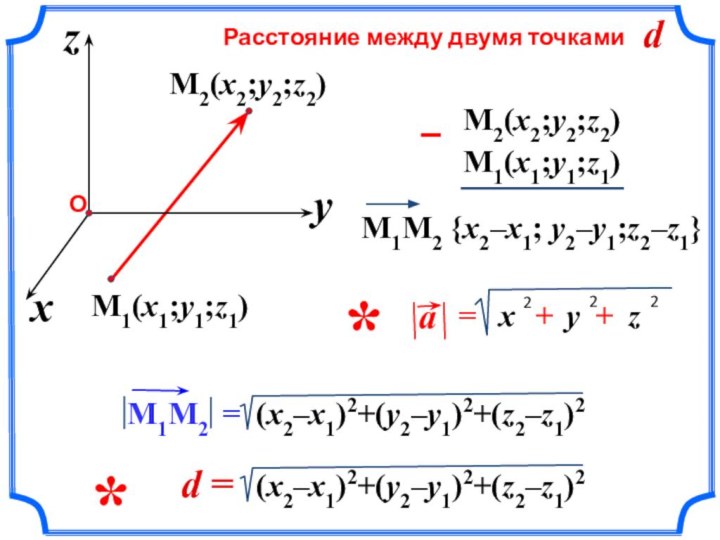
- 17. Расстояние между двумя точками d =d M1(x1;y1;z1)xzyM2(x2;y2;z2)M2(x2;y2;z2)M1(x1;y1;z1)*
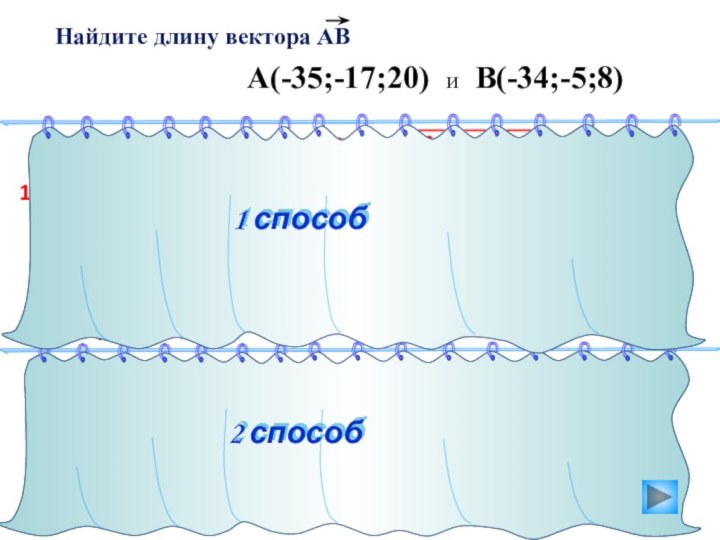
- 18. Найдите длину вектора АВ A(-1;0;2) и B(1;-2;3)1 способ2 способ1)2)B(1;-2;3)A(-1;0;2)= 3
- 19. Скачать презентацию
- 20. Похожие презентации
Цель обучения10.4.2 уметь находить расстояние между двумя точками в пространстве








Слайд 3
Критерии успеха:
записывает формулу расстояния между двумя точками в
пространстве;
применяет формулу расстояния между двумя точками в пространстве при
решении задач.Учащийся
Слайд 4
Повторение:
1. Даны точки А ( - 1; 7
) и В ( 7; 1).
а) Найдите координаты середины
отрезка АВ.С ( 3; 4)
б) Найдите длину отрезка АВ.
|АВ| = 10
Слайд 5
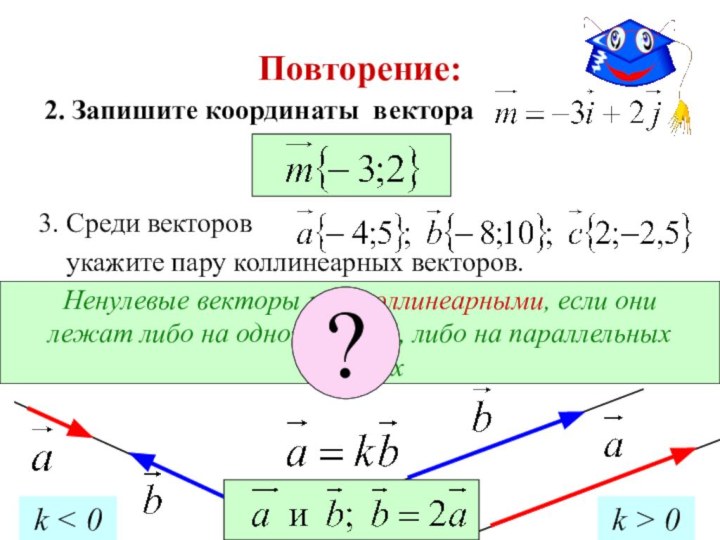
Повторение:
2. Запишите координаты вектора
Ненулевые векторы наз. коллинеарными,
если они
лежат либо на одной прямой, либо на
параллельных прямых
3. Среди векторов
укажите пару коллинеарных векторов.
?
k < 0
k > 0
Слайд 6
Повторение:
4. Найдите координаты вектора
, если
Е ( -2; 3), F
( 1; 2).5. Найдите расстояние между точками
А (а; 0) и В (b; 0).
МОЛОДЦЫ!
Слайд 7
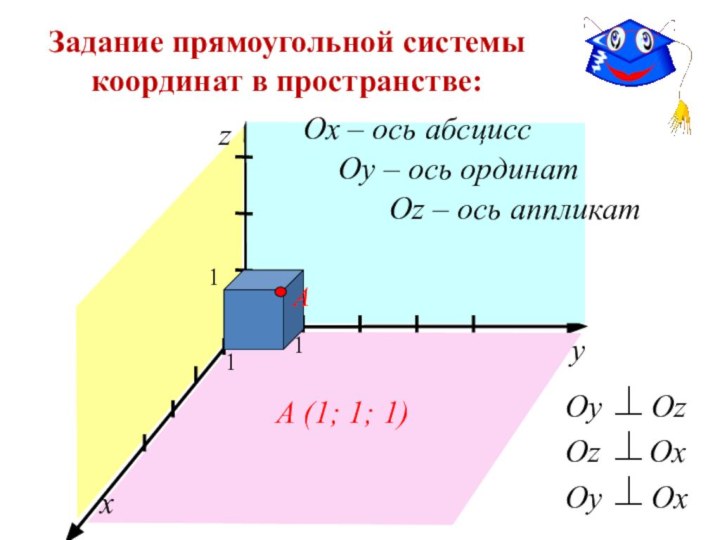
Задание прямоугольной системы
координат в пространстве:
О
y
Оy
Оz
Оz Оx
Оy Оx
x
z
1
1
1
A
A (1; 1;
1)Ох – ось абсцисс
Оу – ось ординат
Оz – ось аппликат
Слайд 8
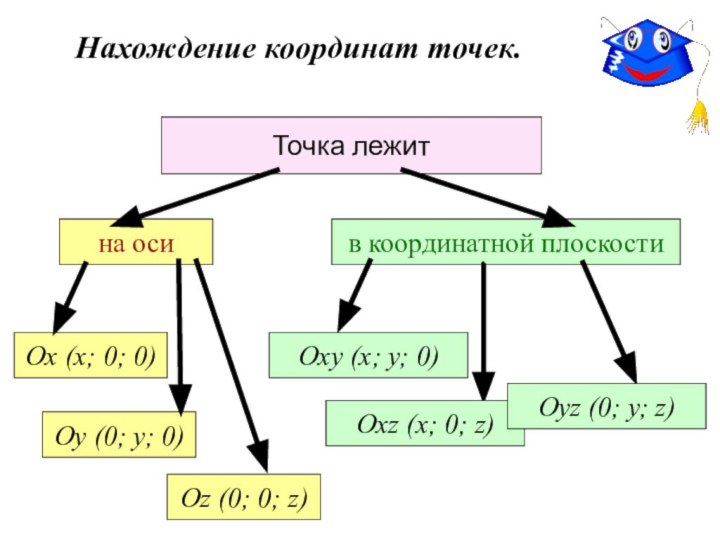
Нахождение координат точек.
Точка лежит
на оси
Оу (0; у; 0)
Ох
(х; 0; 0)
Оz (0; 0; z)
в координатной плоскости
Оху (х;
у; 0)Охz (х; 0; z)
Оуz (0; у; z)
Слайд 9
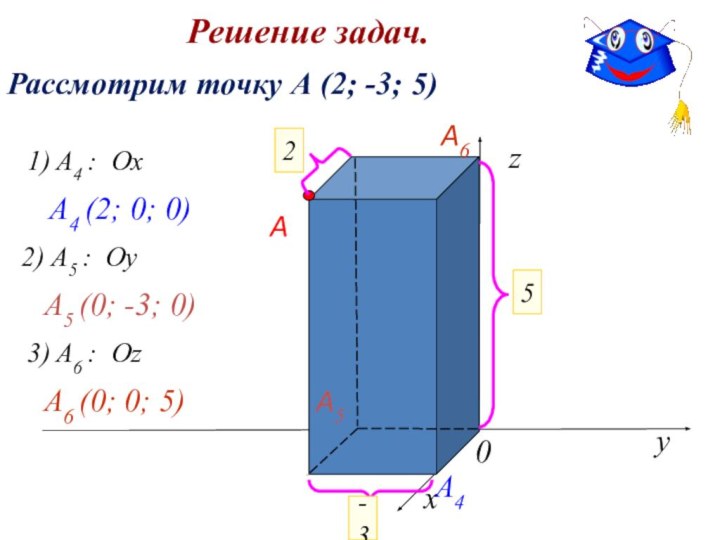
Решение задач.
Рассмотрим точку А (2; -3; 5)
х
у
z
0
2
5
-3
A
1) A4
: Ox
A4
A4 (2; 0; 0)
A5
2) A5 : Oу
A5 (0;
-3; 0)3) A6 : Oz
A6
A6 (0; 0; 5)
Слайд 10
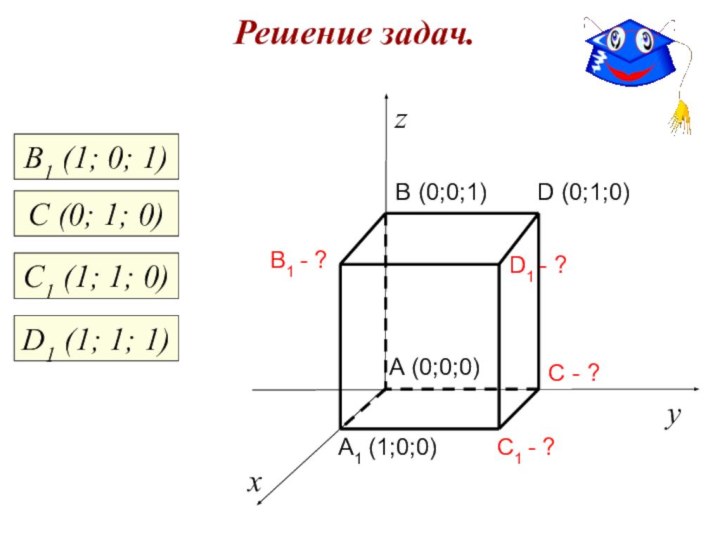
Решение задач.
х
у
z
C1 - ?
C - ?
A1 (1;0;0)
B1 -
?
D1 - ?
A (0;0;0)
B (0;0;1)
D (0;1;0)
В1 (1; 0; 1)
С
(0; 1; 0)С1 (1; 1; 0)
D1 (1; 1; 1)
Слайд 12
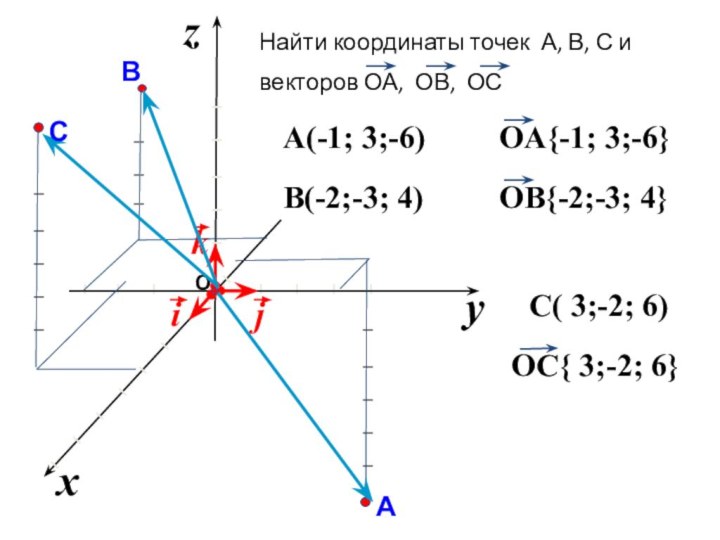
Найти координаты точек А, В, С и
векторов
ОА, ОВ, ОС
A(-1; 3;-6)
B(-2;-3; 4)
y
x
z
I
I I I I I I I I I I I I
I I I I I I I I
O
C( 3;-2; 6)
Слайд 13
x
z
y
{x2-x1; y2-y1; z2-z1}
Каждая координата вектора равна разности
соответствующих
координат его конца и начала.
*
Слайд 14
B
A
(3;5;7),
(5;4;-1),
P
C
(2;-1;0),
(4;-4;2),
D
(-3;-4;0),
R
T
(-4;0;-4),
(0;5;-1),
N
(3;2;-3),
B(5;4;-1)
A(3;5;7)
C(4;-4;2)
P(2;-1;0)
T(0; 5;-1)
R(-4;0;-4)
O
(0;0;0),
O
(0;0;0),
AB
ON
Слайд 15
Найдите координаты
векторов
R(2; 7;1)
M(-2;7;3)
R(2;7;1); M(-2;7;3); RM
P(-5;1;4); D(-5;7;-2); PD
P(-5;
1;4)
D(-5;7;-2)
R(-3;0;-2); N(0;5;-3); RN
A(0;3;4); B(-4;0;-3); BA
R(-7;7;-6); T(-2;-7;0); RT
A(-2;7;5); B(-2;0;-3);
ABR(-3;0;-2)
N(0; 5;-3)
B(-4;0;-3)
A(0; 3;4)
A(-2;7;5)
B(-2;0;-3)
R(-7; 7;-6)
T(-2;-7;0)