- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Аксиомы стереометрии
Содержание
- 2. ОСНОВНЫЕ ПОНЯТИЯРасстояние, точка, прямая, плоскость,Множество.обозначения плоскостей.М – все точки пространства
- 3. Аксиома 1. В пространстве существуют плоскости. Через
- 4. Если две различные плоскости имеют общую точку,
- 5. Если прямая проходит через две точки, лежащие
- 6. Расстояние между двумя точками пространства не зависит
- 7. :F: {отрезков} → R+, удовлетворяющую следующим свойствамРасстояние1.
- 8. 2) Как на гладком столе проверить качество
- 9. Ученик нарисовал четырехугольник АВСDПрямая АD лежит в
- 10. Аксиома 5Каждая плоскость разбивает пространство на два полупространства.
- 11. Концы ломаной, состоящей из двух отрезков, лежат
- 12. Скачать презентацию
- 13. Похожие презентации






![Аксиомы стереометрии :F: {отрезков} → R+, удовлетворяющую следующим свойствамРасстояние1. ∃ [AB] | F([AB]) =](/img/tmb/12/1182447/45d4d5e90cf90237e13433698c7ccc75-720x.jpg)




Слайд 2
ОСНОВНЫЕ ПОНЯТИЯ
Расстояние, точка, прямая, плоскость,
Множество.
обозначения плоскостей.
М – все
точки пространства
Слайд 3
Аксиома 1.
В пространстве существуют плоскости.
Через каждые
три точки пространства проходит плоскость.
АКСИОМЫ
∃α⊂М и ∃β⊂М;
∀{А,
В, С}⊂M ∃α | {А, В, С}⊂α Вопросы
1) Зачем первая часть аксиомы при наличии второй?
Каким утверждением ее можно было заменить?
2) Является ли множество М конечным или бесконечным?
3) Верно ли, что через каждые одну или две точки
пространства проходит плоскость?
4) Докажите, что в пространстве через каждые две точки
проходит прямая.
Следует ли отсюда, что прямые в пространстве можно
обозначать (AB), (CD), ..., как в планиметрии?
Слайд 4
Если две различные плоскости имеют общую точку,
то
их пересечением является прямая.
Аксиома 2.
С∈α, С∈β ⇒ α
β = c Почему С∈с?
Определение.
Две различные плоскости, имеющие общую точку,
называются пересекающимися.
1)Докажите, что ∀α ∃X∉α
2)Докажите существование пересекающихся плоскостей
Определение.
Сечением фигуры F плоскостью α называется их пересечение.
Слайд 5
Если прямая проходит через две точки, лежащие
в
данной плоскости, то она лежит в этой плоскости.
Аксиома
3.A∈α, B∈α и A∈с, B∈с ⇒ с⊂α
Сколько общих точек могут иметь плоскость и прямая,
не лежащая в ней?
Определение.
Прямая и плоскость, имеющие единственную общую точку,
называются пересекающимися.
Докажите их существование
Слайд 6
Расстояние между двумя точками пространства
не зависит от
того, на какой из плоскостей,
содержащих эти точки оно
измерено. Аксиома 4.
∀A∈M, B∈M ∃!|AB|
Почему потребовалась такая аксиома?
Слайд 7
:
F: {отрезков} → R+, удовлетворяющую следующим свойствам
Расстояние
1. ∃
[AB] | F([AB]) = 1.
2. [AB] = [CD] ⇒
F([AB]) = F([CD]).
Как называется такой вид определения?
3. Если точки С1, С2, ..., Сn таковы, что взятые в этом
порядке, они разбивают [AB] на отрезки, не имеющие общих
внутренних точек,
то F([AB]) = F([AC1]) + F([C1C2]) + ... + F([CnB]).
Слайд 8
2) Как на гладком столе проверить качество
изготовления
линейки?
На чем основан ваш способ проверки?
Как решить
обратную задачу? 1) Из одной точки одновременно разных направлениях вылетели три вороны со скоростями 1, 2 и 3 метра в секунду.
В какой момент после вылета они окажутся
в одной плоскости?
Слайд 9
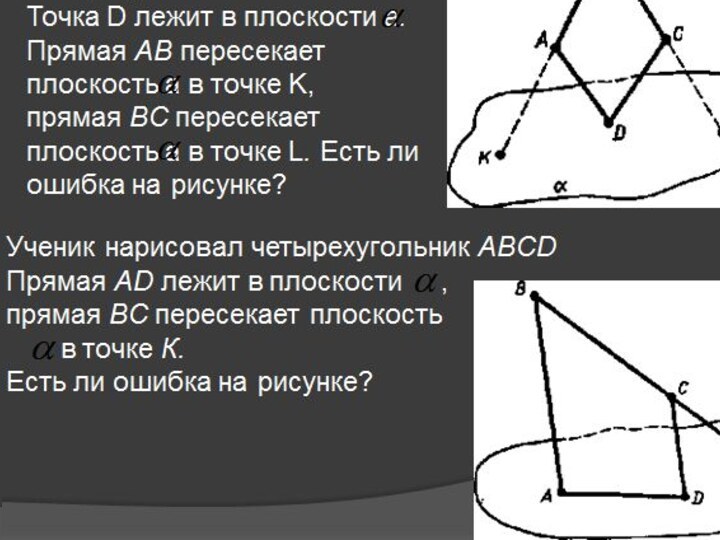
Ученик нарисовал четырехугольник АВСD
Прямая АD лежит в плоскости
,
прямая ВС пересекает плоскость
в точке К. Есть ли ошибка на рисунке?
Ученик нарисовал четырехугольник АВСD
Точка D лежит в плоскости а.
Прямая AВ пересекает плоскость а в точке K,
прямая ВС пересекает плоскость а в точке L. Есть ли ошибка на рисунке?
Слайд 11
Концы ломаной, состоящей из двух отрезков,
лежат по
разные стороны от данной плоскости.
Докажите, что она пересекает
эту плоскость. Обобщите это утверждение
Имеется п плоскостей.
Имеют ли они все общую точку, если:
а) каждые две из них имеют общую точку;
б) каждые три из них имеют общую точку?