- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Другие признаки равенства треугольников
Содержание
- 2. Цель работы: найти другие признаки равенства треугольников, прохождение которых не входит в школьную программу.
- 3. Признаки:По углу, прилежащей к нему стороне, и сумме длин двух сторон.«Косой» признак равенства треугольников.
- 4. Два треугольника равны, если угол, прилежащая к
- 5. Доказательство:Дополнительное построение: Продлим отрезок СА за точку
- 6. Получившиеся ΔАВD и ΔА1В1D1 – равнобедренные (по
- 8. Если две стороны первого треугольника соответственно равны
- 9. Пусть имеются два треугольника: Δ ABC
- 10. Приложим Δ ABC к Δ A1B1C1 так,
- 11. Так как в четырехугольнике A1B1C1B имеются равные
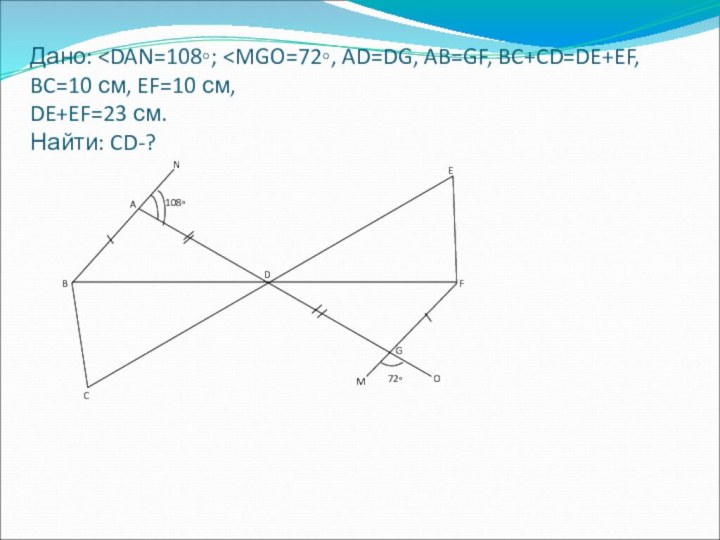
- 12. Дано:
- 13. 1)⦟BAD=72˚(св. смеж. угл.), ⦟DGF=72˚ (св. верт. угл.)2)∆BAD=∆DGF(по
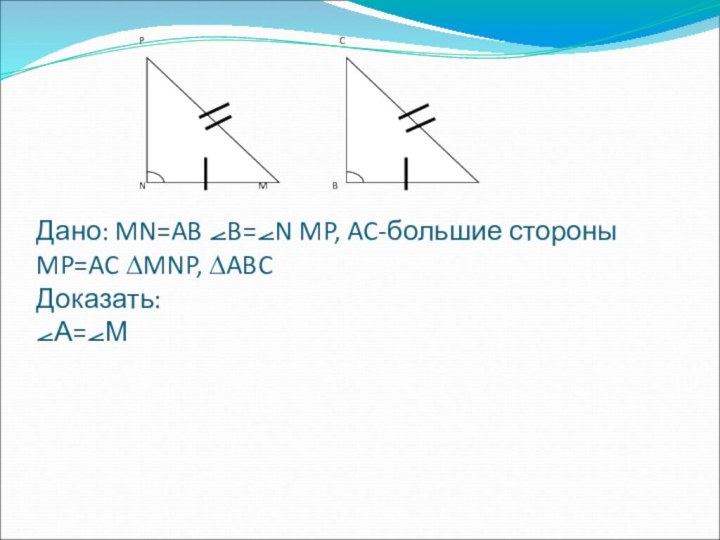
- 14. Дано: MN=AB ⦟B=⦟N MP, AC-большие стороны MP=AC ∆MNP, ∆ABC Доказать: ⦟А=⦟М
- 15. Скачать презентацию
- 16. Похожие презентации
Цель работы: найти другие признаки равенства треугольников, прохождение которых не входит в школьную программу.








Слайд 2
Цель работы: найти другие признаки равенства треугольников,
прохождение которых не входит в школьную программу.
Слайд 3
Признаки:
По углу, прилежащей к нему стороне, и сумме
длин двух сторон.
«Косой» признак равенства треугольников.
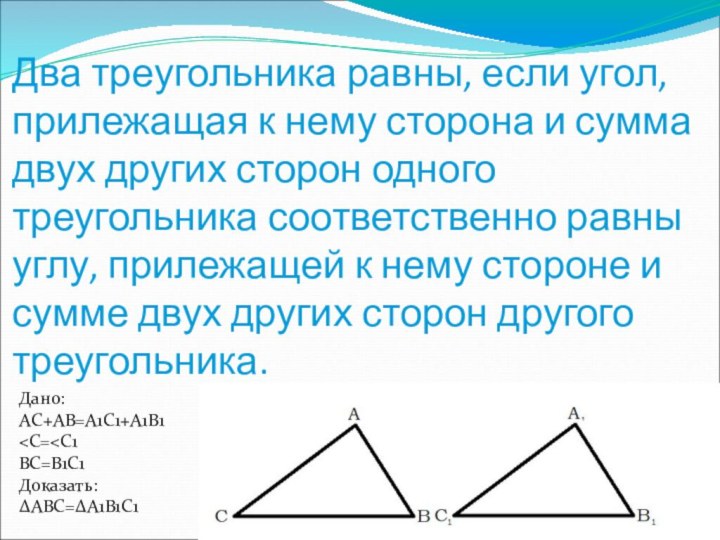
Слайд 4 Два треугольника равны, если угол, прилежащая к нему
сторона и сумма двух других сторон одного треугольника соответственно
равны углу, прилежащей к нему стороне и сумме двух других сторон другого треугольника.Дано:
AС+AB=A1С1+A1B1
Доказать:
ΔABC=ΔA1B1C1
Слайд 5
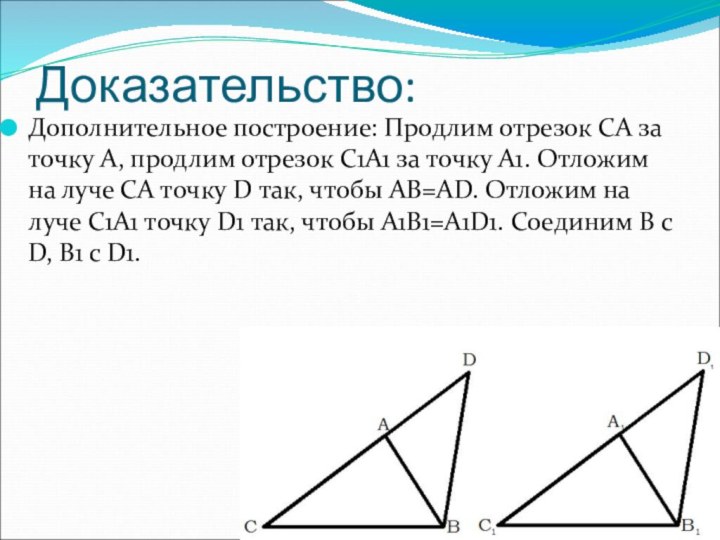
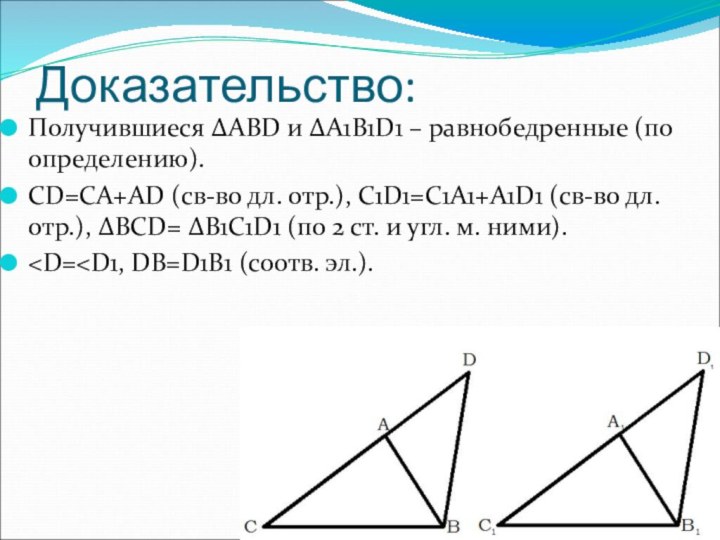
Доказательство:
Дополнительное построение: Продлим отрезок СА за точку А,
продлим отрезок С1А1 за точку А1. Отложим на луче
СА точку D так, чтобы АВ=АD. Отложим на луче С1А1 точку D1 так, чтобы А1В1=А1D1. Соединим В с D, В1 с D1.
Слайд 6
Получившиеся ΔАВD и ΔА1В1D1 – равнобедренные (по определению).
СD=СА+АD
(св-во дл. отр.), С1D1=С1А1+А1D1 (св-во дл. отр.), ΔВСD= ΔВ1С1D1
(по 2 ст. и угл. м. ними).Доказательство:
Слайд 7
– равнобедренный.
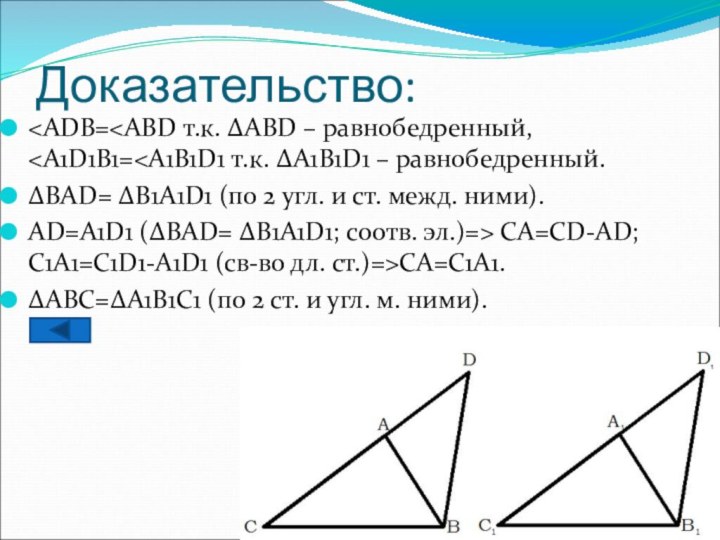
ΔВАD= ΔВ1А1D1 (по 2 угл. и ст. межд.
ними).АD=A1D1 (ΔВАD= ΔВ1А1D1; соотв. эл.)=> CА=СD-AD; C1А1=С1D1-A1D1 (св-во дл. ст.)=>CA=C1A1.
ΔABC=ΔA1B1C1 (по 2 ст. и угл. м. ними).
Доказательство:
Слайд 8 Если две стороны первого треугольника соответственно равны двум
сторонам второго треугольника и угол, противолежащий большей из этих
сторон в первом треугольнике, равен углу, противолежащему соответственно равной ей стороне во втором треугольнике, то эти треугольники равны.
Слайд 9
Пусть имеются два треугольника: Δ ABC и
Δ A1B1C1, причем AB = A1B1, AC = A1C1,
Слайд 10
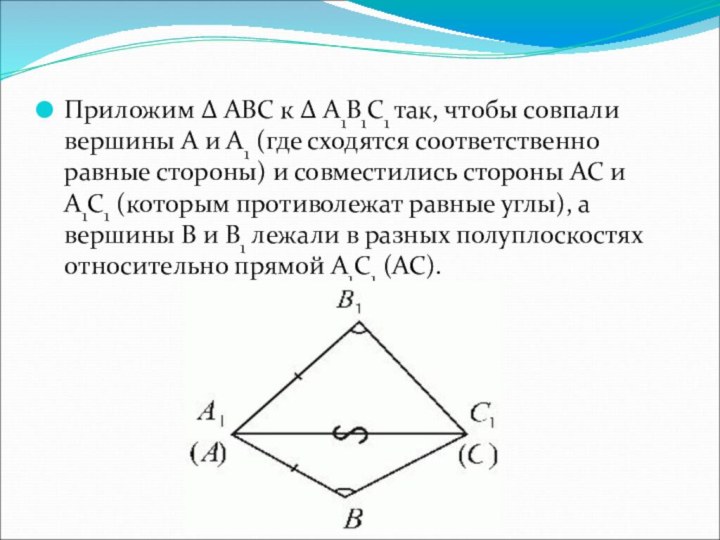
Приложим Δ ABC к Δ A1B1C1 так, чтобы
совпали вершины A и A1 (где сходятся соответственно равные
стороны) и совместились стороны AC и A1C1 (которым противолежат равные углы), а вершины B и B1 лежали в разных полуплоскостях относительно прямой A1C1 (AC).
Слайд 11
Так как в четырехугольнике A1B1C1B имеются равные стороны
и углы, возникает мысль использовать свойства равнобедренного треугольника. Для
этого соединим отрезком вершины В1 и В.ΔAB1B – равнобедренный =>
ренный (по пр.)=> B1C=
=BC (по опред.).
ΔАBC= ΔA1B1C1 (по 2 ст.
и угл. м. ними).
Слайд 13
1)⦟BAD=72˚(св. смеж. угл.), ⦟DGF=72˚ (св. верт. угл.)
2)∆BAD=∆DGF(по 2
ст. и угл. м. ними)=>BD=DF(соотвеств. эл.)
3) ⦟BDC=⦟EDF(св. верт. угл.)
4)
Имеем: BD=DF(см. п.2), BC+CD=DE+EF(по усл.), ⦟BDC=⦟EDF(см.п.3)=> ∆BCD=∆DEF(по углу, прилежащей к нему стороне, и сумме длин двух сторон).5)т.к. DE+EF=23 см, а EF=10 см=>DE=13 cм (св. дл. отр.)=>CD=13 см(CD=DE)
Ответ: CD=13 см.