этих полупространств будем называть
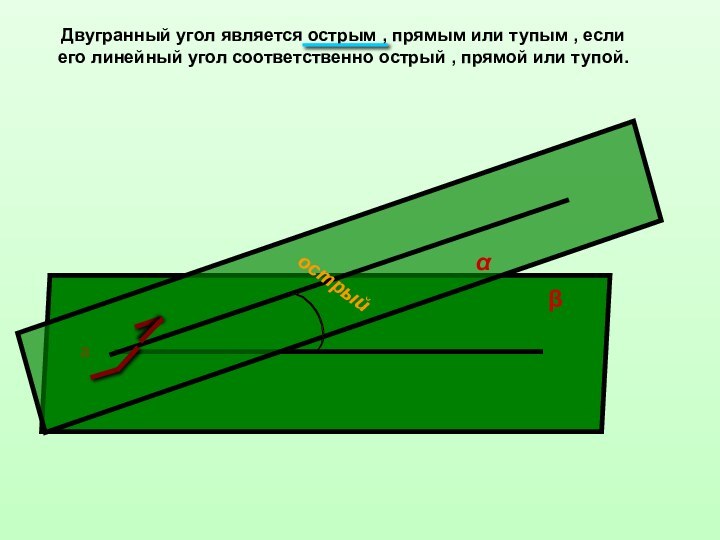
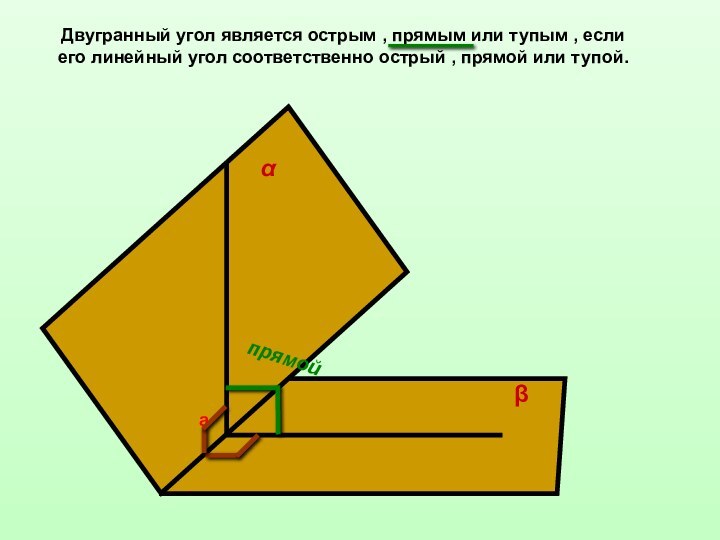
двугранным углом
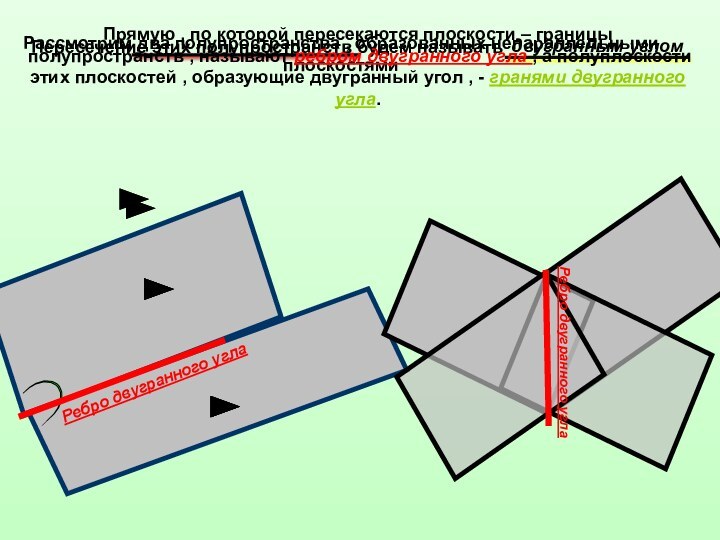
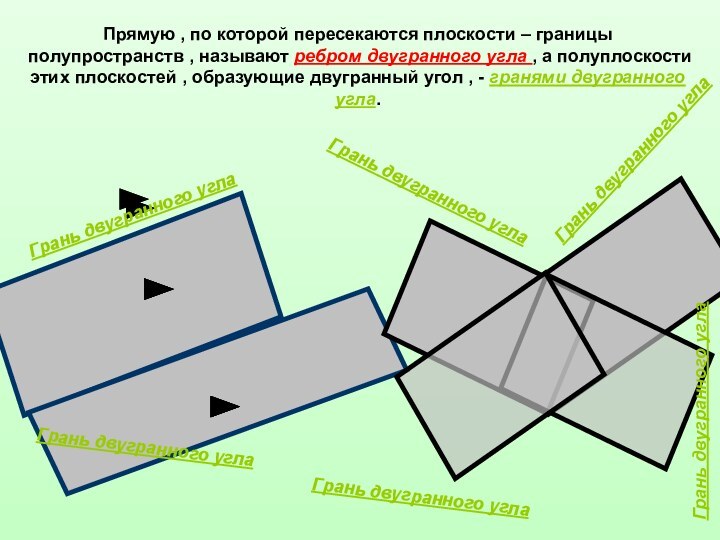
Прямую , по которой
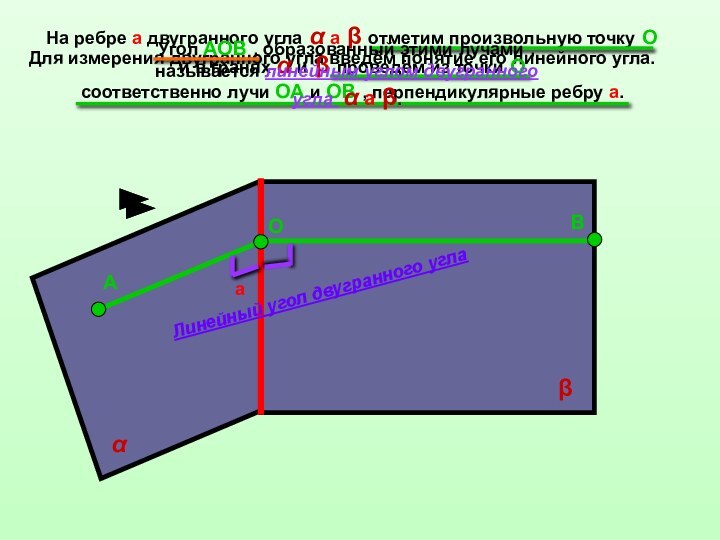
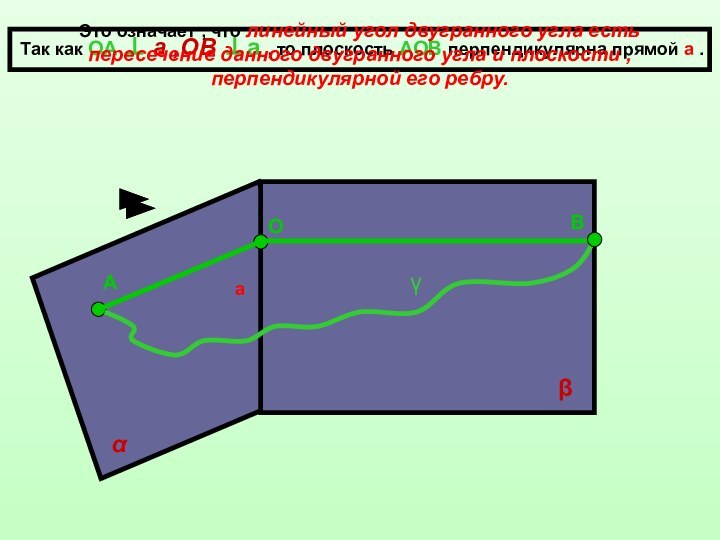
пересекаются плоскости – границы полупространств , называют ребром двугранного угла , а полуплоскости этих плоскостей , образующие двугранный угол , - гранями двугранного угла.Ребро двугранного угла
Ребро двугранного угла

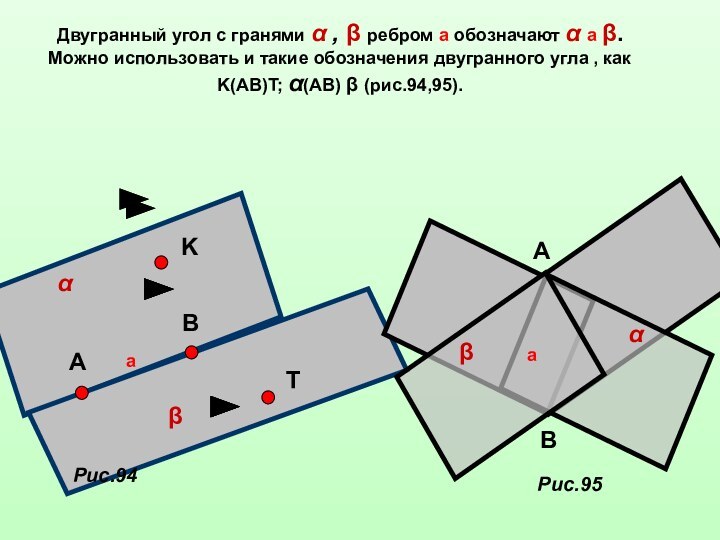

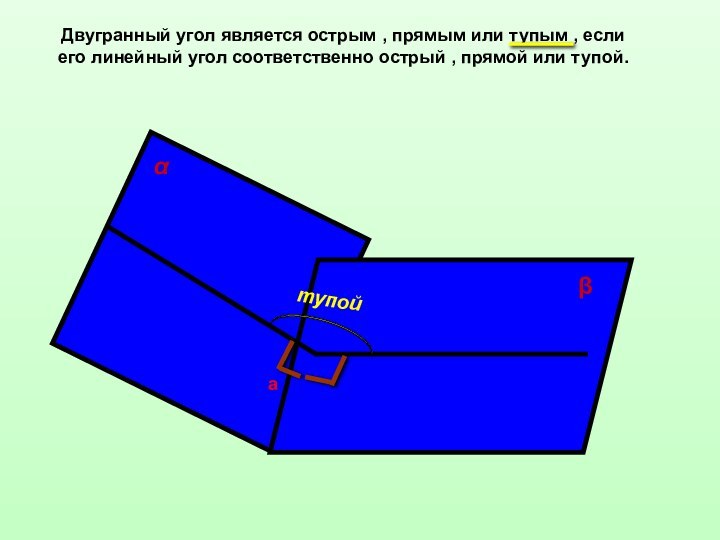
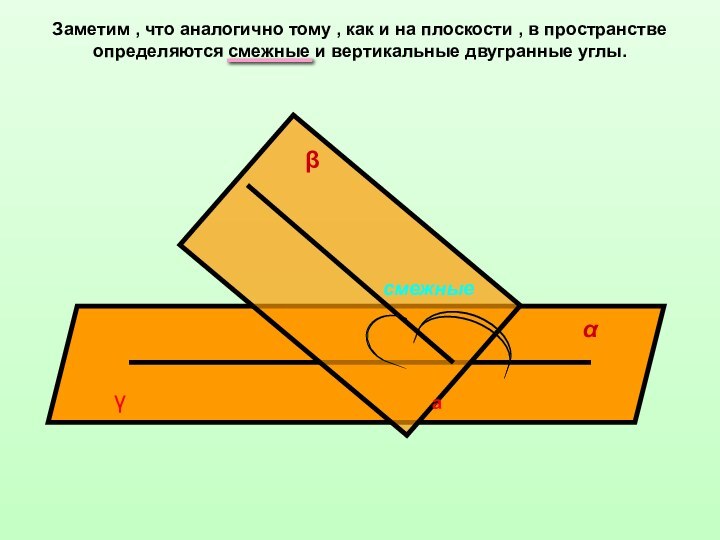
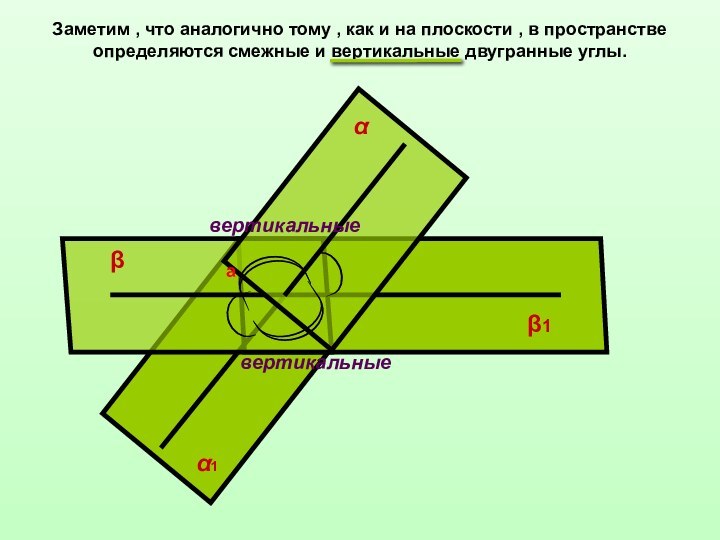

![Двугранные углы ββ1аαα1сϕВеличина угла между плоскостями принадлежит промежутку [0°;90°].](/img/tmb/12/1195400/4e1b0a2b0b3af21aca4229bf6b72c260-720x.jpg)