Презентация на тему к уроку геометрия 9 класс Синус,косинус, тангенс, котангенс

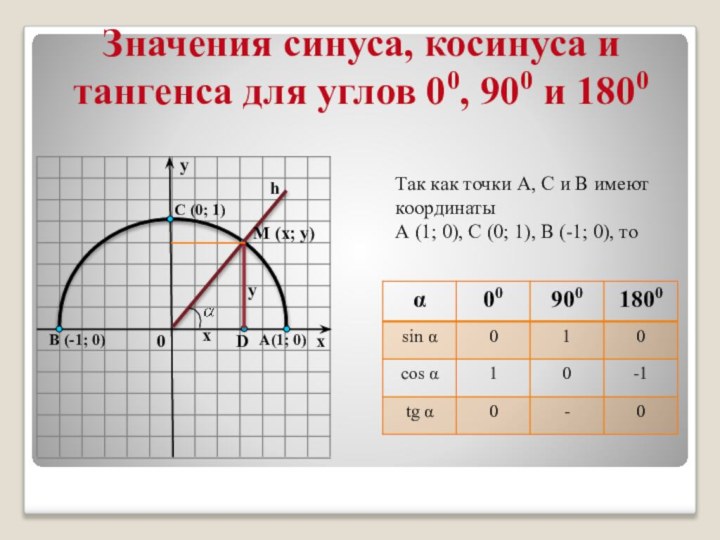
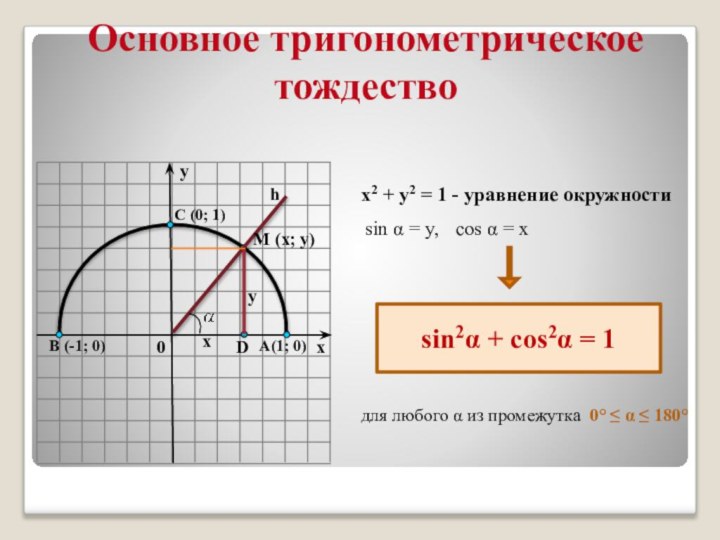
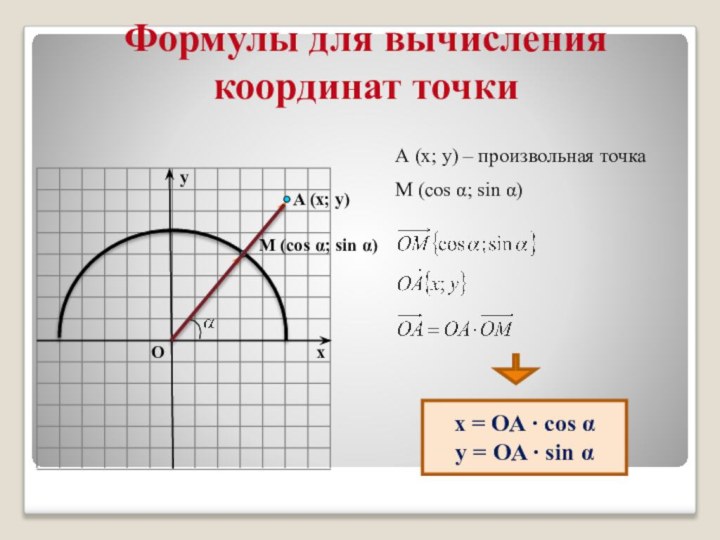
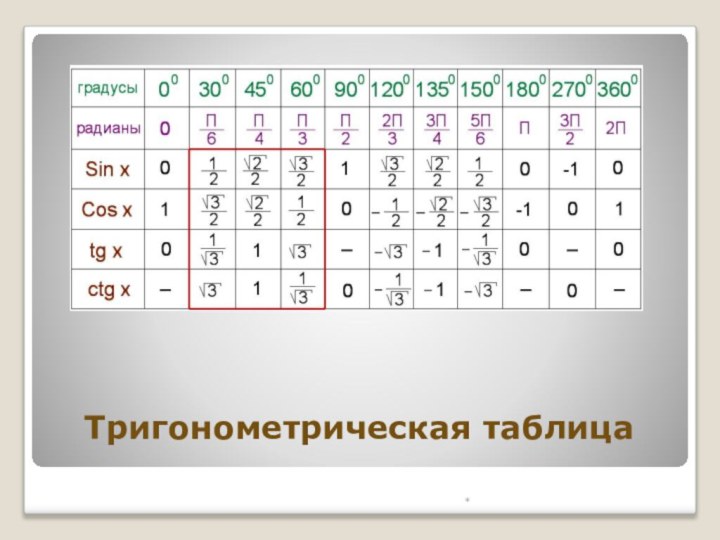
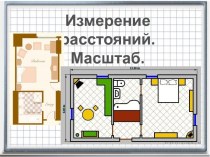
умеют осуществлять контроль по результату и способу действия на

уровне произвольного внимания и вносить необходимые коррективы.
Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, ясно, точно, грамотно излагать свои мысли.
Личностные: понимают важность и необходимость изучения предмета в жизни человека

*

математике,- это быть точным, второе- быть ясным и ,

насколько возможно, простым».
Л.Карно(19век Франция)

*

прямоугольного треугольника?
2. Какое равенство называют основным тригонометрическим тождеством?

3. Чему равны значения синуса, косинуса и тангенса для углов 30°, 45° и 60°?

*

основное тригонометрическое тождество

*

в начале координат, а радиус равен 1.









M (x; y)
C

(0; 1)

B (-1; 0)

A(1; 0)

x

y

O

x

y

D

h

прямоугольный
MD = y
OM = 1

sin α = y
Синус угла

– ордината у точки М

cos α =

OD = x

OM = 1

cos α = x

Косинус угла – абсцисса х точки М

Синус, косинус, тангенс угла

tg α =

MD = y = sin α

OD = x = cos α

в промежутках
0 ≤ у ≤ 1, - 1 ≤

х ≤ 1,

то для любого α из промежутка

0° ≤ α ≤ 180°

справедливы неравенства:

0 ≤ sin α ≤ 1,
- 1≤ cos α ≤ 1

900 и 1800
Так как точки А, С и B

имеют координаты
А (1; 0), С (0; 1), В (-1; 0), то

уравнение окружности
sin α = y,
cos α = x

sin2α +

cos2α = 1

для любого α из промежутка 0° ≤ α ≤ 180°

- α) = cos α

cos (90° - α) =

sin α

sin (180° - α)= sin α

cos (180° - α) = - cos α

при 0° ≤ α ≤ 180°

вычисления координат точки

А (x; y) – произвольная точка
М (сos

α; sin α)

x = ОА ∙ cos α
y = OA ∙ sin α

понятие функции и принятую в наши дни символику.

Он придал всей тригонометрии ее современный вид.

и в тетрадях.
№1013

*

единичной полуокружности, если выполняются условия: –1≤х ≤1, –1≤у ≤1

и х2 + у2 = 1.
Точка М1 (0; 1) удовлетворяет всем условиям → она лежит на единичной полуокружности.
Точка М2 удовлетворяет всем условиям →она лежит на единичной полуокружности.
Точки М3 , М4 , А(1; 0), В(–1; 0) также лежат на единичной

полуокружности.
Синус <АОМ – это ордината точки М. Косинус <АОМ – это абсцисса точки М. Тангенс <АОМ равен отношению синуса <АОМ к его косинусу.
М1(0; 1)→sin<АОМ1 = 1, cos<АОМ1 = 0, tg<АОМ1 = 0.
М2 →sin<АОМ2 = , cos<АОМ2 = , tg<АОМ2 = : = √3

М3 →sin<АОМ3 = , cos<АОМ3 = , tg<АОМ3 =


М4 →sin<АОМ4 = , cos<АОМ4 = , tg<АОМ4 =

*

=

, но так как 0 ≤sina ≤1 →sina = .
а) cosa = → sina =
б) cosa = → sina =
в) cosa = –1 → sina = 0.


Ответ: а) ; б) ; в) 0

*

существительное или местоимение, которое обозначает объект или предмет, о

котором пойдет речь.
2 строка - два слова, чаще всего прилагательные или причастия. Они дают описание признаков и свойств выбранного в синквейне предмета или объекта.
3 строка - образована тремя глаголами или деепричастиями, описывающими характерные действия объекта.
4 строка - фраза из четырех слов, выражает личное отношение автора синквейна к описываемому предмету или объекту.
5 строка - одно слово, характеризующее суть предмета или объекта.