- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии на тему Поверхности вращения
Содержание
- 2. Поверхность – одно из основных геометрических понятий!!!В
- 3. 2) В начертательной геометрии геометрические фигуры задаются
- 4. Виды поверхностейЛинейчатые(образующая – прямая линия)Не линейчатые(образующая –
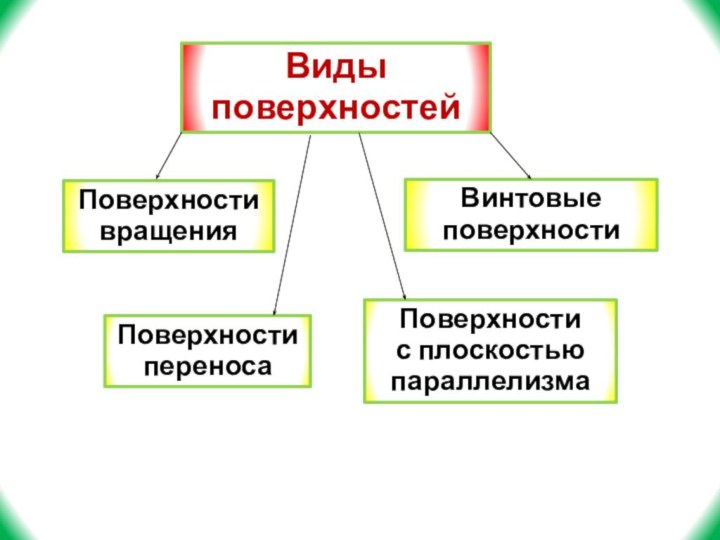
- 5. Виды поверхностейПоверхности вращенияВинтовые поверхностиПоверхности переносаПоверхности с плоскостью параллелизма
- 6. Образование поверхности вращения.
- 7. Поверхности вращения – это поверхности ,созданные
- 8. Так создается каркас поверхности, состоящей из множества
- 9. Наиболее распространенные поверхности вращения с криволинейными образующими.Сфера
- 10. Тор образуется при вращении окружности вокруг оси,
- 11. Гиперболоид вращения. Различают однополостной и двухполостной гиперболоиды
- 12. Волчок Миндингаи его график меридиана.
- 13. Катушка Миндингаи её график меридиана.
- 14. Псевдосфераи её график меридиана.
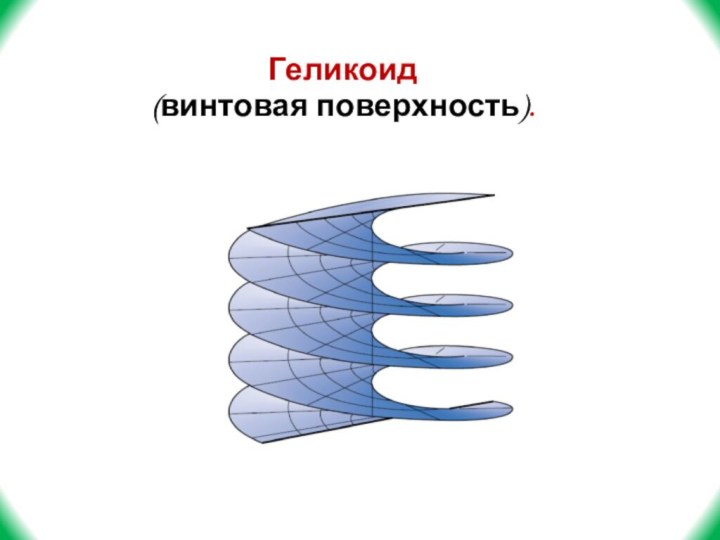
- 15. Геликоид(винтовая поверхность).
- 16. Когда люди стали строить здания из
- 17. Скалками цилиндрической формы пользовались и женщины, раскатывая
- 18. Цилиндр — геометрическое тело, полученное путем
- 19. Бесконечное тело, ограниченное замкнутой бесконечной цилиндрической поверхностью,
- 20. Конечное тело, ограниченное замкнутой конечной цилиндрической поверхностью
- 21. rоснование цилиндрабоковая поверхность цилиндраоснование цилиндраобразующая цилиндраось цилиндра
- 22. Поперечное сечение.круг
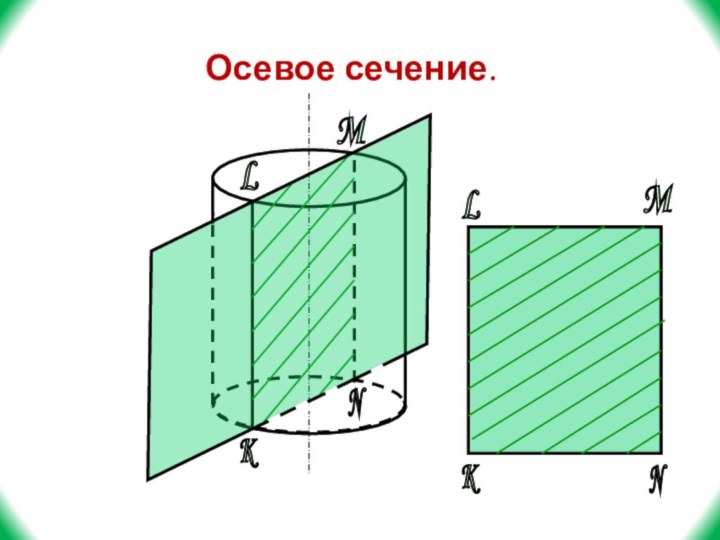
- 23. Осевое сечение.M
- 24. Конус -с греческого “konos”“сосновая шишка”. С конусом
- 25. «Конусами» называется семейство морских моллюсков.В геологии существует
- 26. ABCCC12C3Конус – тело, полученное вращением прямоугольного треугольника вокруг одного из катетов.
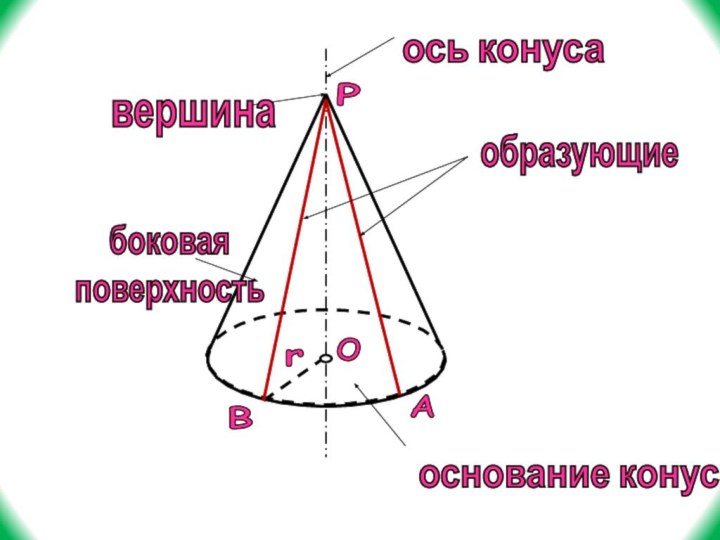
- 27. POBArось конусавершинаобразующиеоснование конусабоковаяповерхность
- 28. Поперечное сечение конуса.круг
- 29. Осевое сечение конуса.
- 30. сечение – эллипсСечение -фигура, ограниченная параболой и хордой основания
- 31. Сечение -фигура, ограниченная гиперболой и хордой основания
- 32. Большой трактат о конических сечениях был написан
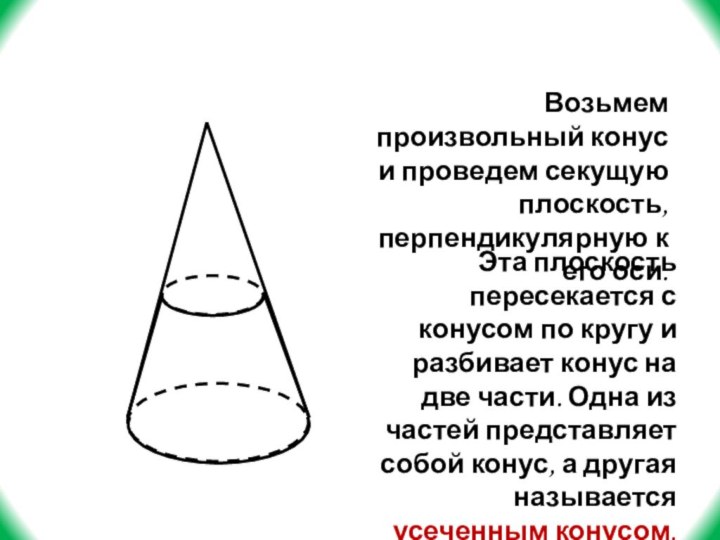
- 33. Возьмем произвольный конус и проведем секущую плоскость,
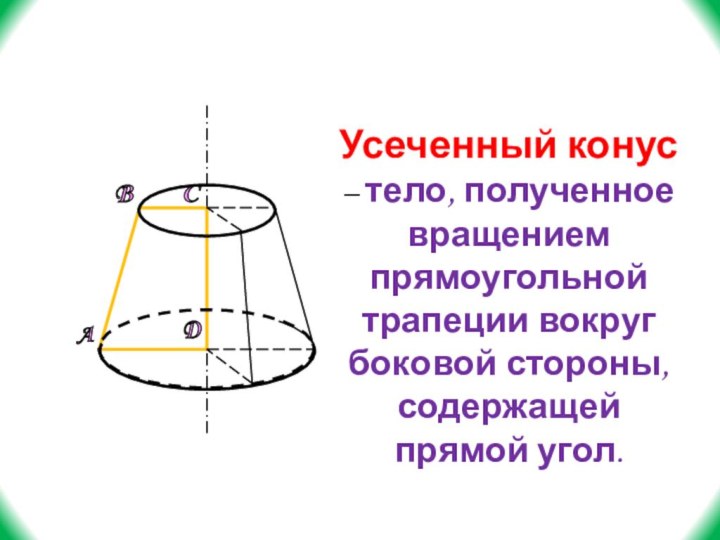
- 34. ABCDУсеченный конус – тело, полученное вращением прямоугольной трапеции вокруг боковой стороны, содержащей прямой угол.
- 35. По-гречески так назывался мяч, с которым играли
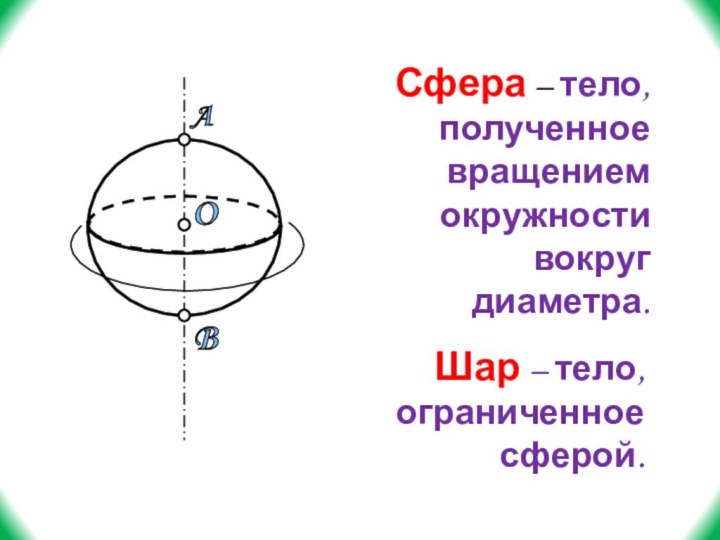
- 36. ABOСфера – тело, полученное вращением окружности вокруг диаметра.Шар – тело, ограниченное сферой.
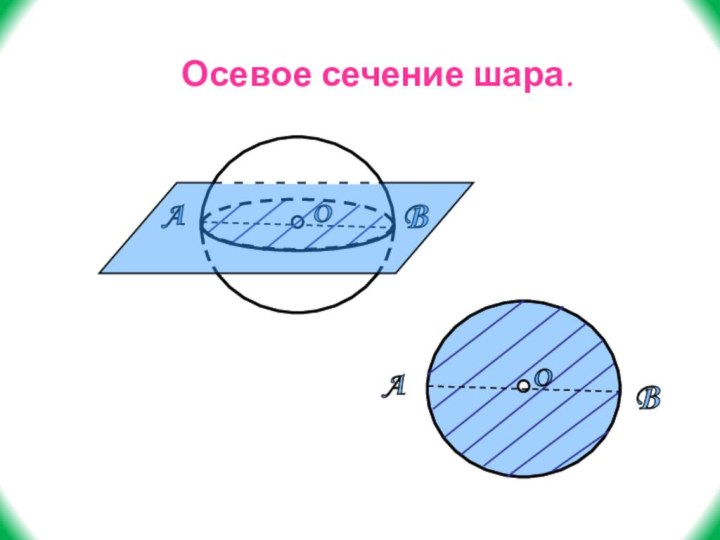
- 37. OABОсевое сечение шара.
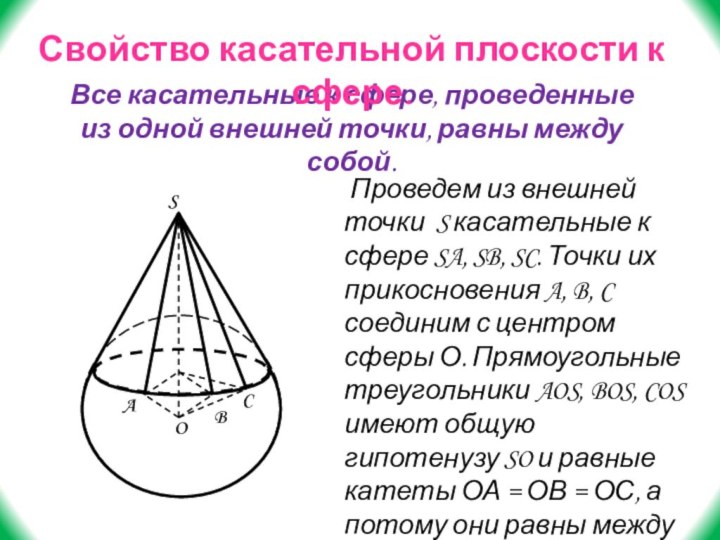
- 38. Все касательные к сфере, проведенные из одной
- 39. 1) Если d
- 40. 2) Если d = R, то сфера
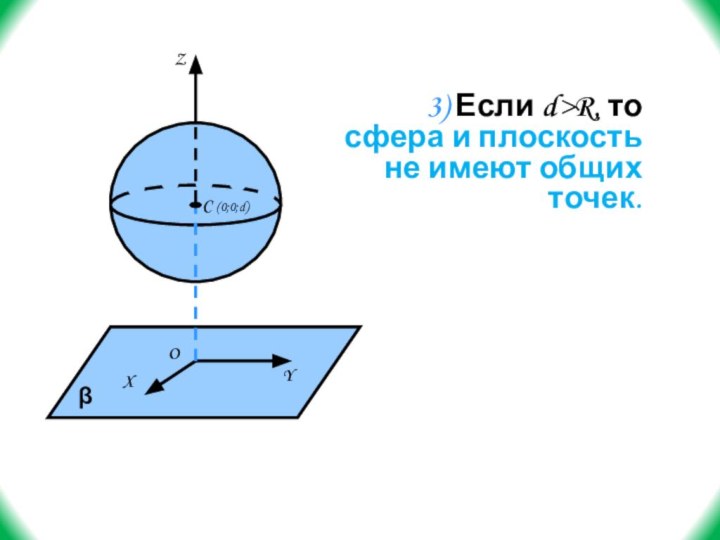
- 41. 3) Если d>R, то сфера и плоскость не имеют общих точек.
- 42. Сферическая тригонометрия - область математики в
- 43. Сферическая астрономия – раздел астрономии, разрабатывающий
- 44. Архимед доказал, что любые две плоскости,
- 45. Трехгранный угол с вершиной в центре сферы
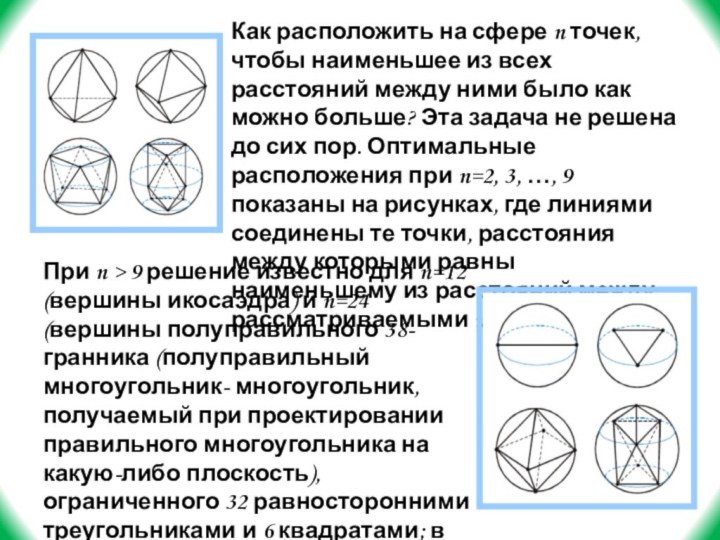
- 46. Как расположить на сфере n точек, чтобы
- 47. Скачать презентацию
- 48. Похожие презентации
Поверхность – одно из основных геометрических понятий!!!В математике под поверхностью подразумевается непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая в декартовой системе координат уравнением вида F(x, у, z) = 0, где F(x, у,
Слайд 3 2) В начертательной геометрии геометрические фигуры задаются графически,
поэтому целесообразно рассматривать поверхность как совокупность всех последовательных положений
некоторой перемещающейся в пространстве линии.3) В школьном курсе геометрии рассматриваются некоторые кривые поверхности. Каждая из кривых поверхности определяется специальным способом, чаще всего как множество точек, удовлетворяющих некоторым условиям. Например, поверхность шара - множество точек, находящихся на заданном расстоянии от данной точки. Понятие "Поверхность" лишь поясняется, а не определяется. Например, говорят, что поверхность есть граница тела или след движущейся линии.
Слайд 4
Виды
поверхностей
Линейчатые
(образующая – прямая линия)
Не линейчатые
(образующая – кривая
линия)
Развертывающиеся
(можно без складок и разрывов развернуть на плоскость )
Не
развертывающиеся
Слайд 5
Виды
поверхностей
Поверхности вращения
Винтовые поверхности
Поверхности
переноса
Поверхности
с плоскостью параллелизма
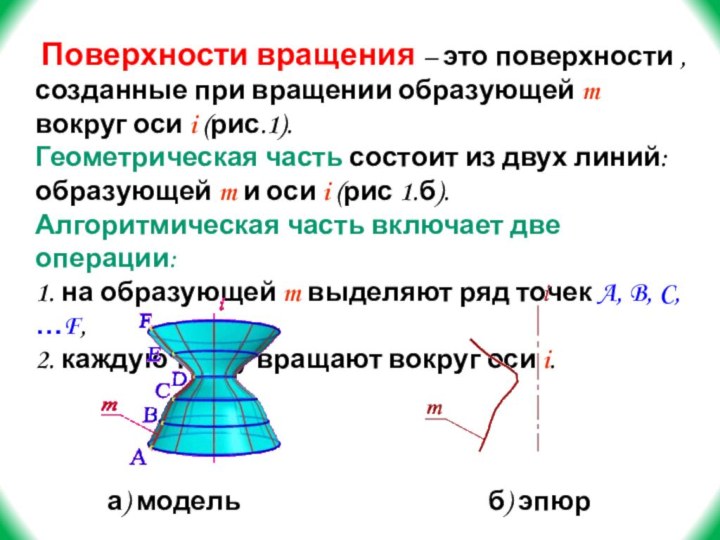
Слайд 7 Поверхности вращения – это поверхности ,созданные при
вращении образующей m вокруг оси i (рис.1).
Геометрическая часть состоит
из двух линий: образующей m и оси i (рис 1.б).Алгоритмическая часть включает две операции:
1. на образующей m выделяют ряд точек A, B, C, …F,
2. каждую точку вращают вокруг оси i.
а) модель
б) эпюр
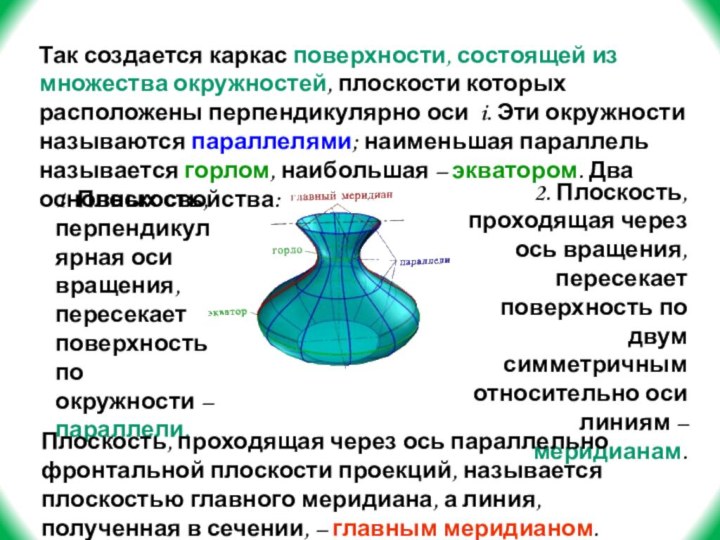
Слайд 8 Так создается каркас поверхности, состоящей из множества окружностей,
плоскости которых расположены перпендикулярно оси i. Эти окружности называются
параллелями; наименьшая параллель называется горлом, наибольшая – экватором. Два основных свойства:1. Плоскость, перпендикулярная оси вращения, пересекает поверхность по окружности – параллели.
2. Плоскость, проходящая через ось вращения, пересекает поверхность по двум симметричным относительно оси линиям – меридианам.
Плоскость, проходящая через ось параллельно фронтальной плоскости проекций, называется плоскостью главного меридиана, а линия, полученная в сечении, – главным меридианом.
Слайд 9
Наиболее распространенные поверхности вращения с криволинейными образующими.
Сфера –
образуется вращением окружности вокруг её диаметра. При сжатии или
растяжении сферы она преобразуется в эллипсоиды, которые могут быть получены вращением эллипса вокруг одной из осей: если вращение вокруг малой оси, то эллипсоид называется сжатым или сфероидом, если вокруг большой – вытянутым.Образование сферы
Образование сфероида
Образование вытянутого
эллипсоида
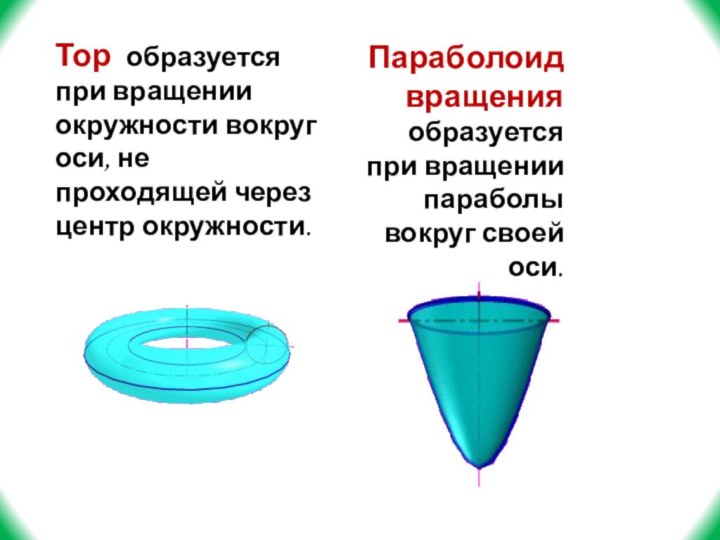
Слайд 10 Тор образуется при вращении окружности вокруг оси, не
проходящей через центр окружности.
Параболоид вращения образуется при вращении параболы
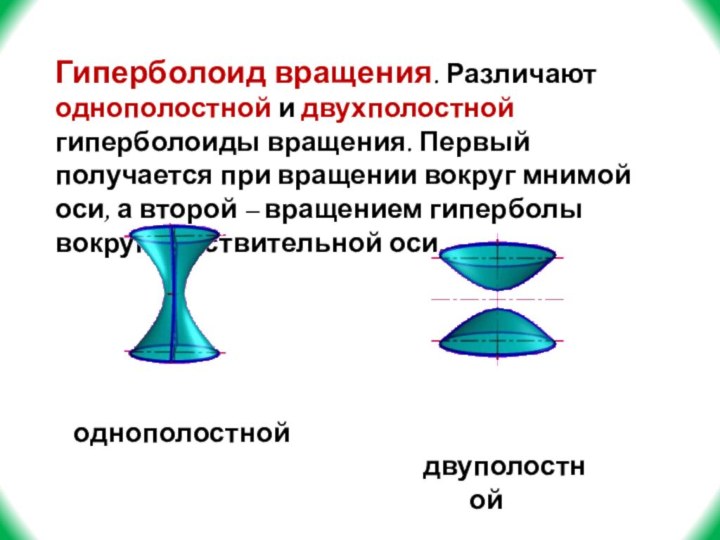
вокруг своей оси.Слайд 11 Гиперболоид вращения. Различают однополостной и двухполостной гиперболоиды вращения.
Первый получается при вращении вокруг мнимой оси, а второй
– вращением гиперболы вокруг действительной оси. однополостной
двуполостной
Слайд 16 Когда люди стали строить здания из камня,
пришлось перетаскивать тяжелые каменные глыбы. Для этого издавна применяли
катки. И было замечено, что перекатка тяжелого камня становится легче, если для катка взято прямое дерево и от него отрезан кусок с почти одинаковой толщиной в начале и в конце. Так люди познакомились с одной из важнейших фигур – цилиндром (греч. kýlindros, валик, каток).Цилиндр.
Слайд 17 Скалками цилиндрической формы пользовались и женщины, раскатывая белье
после стирки.
Перевозить грузы на катках стало довольно трудно, потому
что сами древесные стволы весили много. Чтобы облегчить работу, стали вырезать из стволов тонкие круглые пластики и с их помощью перетаскивали грузы. Так появилось первое колесо. Это было замечательным открытием.
Слайд 18
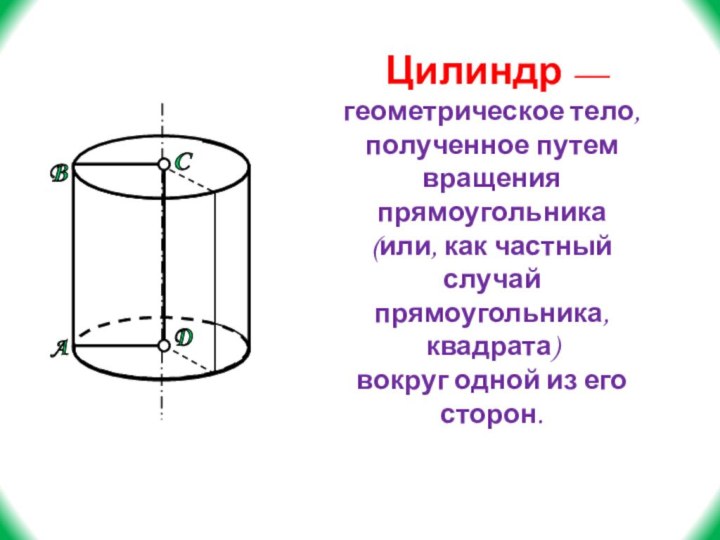
Цилиндр —
геометрическое тело, полученное путем вращения
прямоугольника
(или, как частный случай прямоугольника, квадрата)
вокруг одной из его
сторон.A
B
C
D
Слайд 19 Бесконечное тело, ограниченное замкнутой бесконечной цилиндрической поверхностью, называется
бесконечным цилиндром.
Бесконечное тело, ограниченное замкнутым цилиндрическим лучом и его
основанием, называется открытым цилиндром. Основание и образующие цилиндрического луча называют соответственно основанием и образующими открытого цилиндра.
Слайд 20
Конечное тело, ограниченное замкнутой конечной цилиндрической поверхностью и
двумя выделившими её сечениями, называется конечным цилиндром, или собственно
цилиндром.Сечения называются основаниями цилиндра. По определению конечной цилиндрической поверхности, основания цилиндра равны.
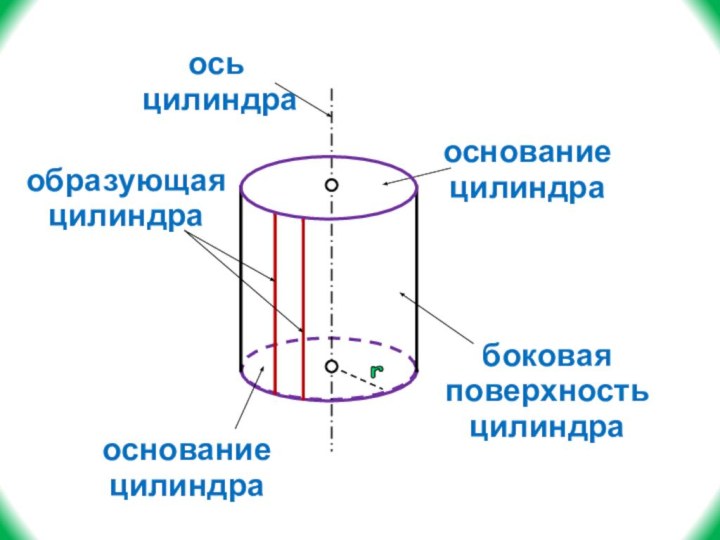
Слайд 21
r
основание цилиндра
боковая поверхность цилиндра
основание цилиндра
образующая цилиндра
ось
цилиндра
Слайд 24 Конус -с греческого “konos”“сосновая шишка”. С конусом люди
знакомы с глубокой древности. В 1906 году была обнаружена
книга Архимеда (287-212 гг. до н.э.) “О методе”, в которой дается решение задачи об объеме общей части пересекающихся цилиндров. Архимед приписывает честь открытия этого принципа Демокриту (470-380 гг. до н.э.) – древнегреческому философу. С помощью этого принципа Демокрит получил формулы для вычисления объема пирамиды и конуса.Конус.
Слайд 25
«Конусами» называется семейство морских моллюсков.
В геологии существует понятие
«конус выноса» вынесение породы горными реками.
В биологии есть понятие
«конус нарастания». Это верхушка побега. Громоотводы создают вокруг себя «конус безопасности». Чем выше громоотвод, тем больше объем такого конуса.
Разные определения конуса.
Слайд 26
A
B
C
C
C
1
2
C
3
Конус – тело, полученное вращением прямоугольного треугольника вокруг
одного из катетов.
Слайд 32 Большой трактат о конических сечениях был написан Аполлонием
Пергским (260-170 гг. до н.э.) – учеником Евклида (II
в. до н.э.), который создал великий труд из 15 книг под названием “Начала”. Эти книги издаются и по сей день, а в школах Англии по ним учатся.Слайд 33 Возьмем произвольный конус и проведем секущую плоскость, перпендикулярную
к его оси.
Эта плоскость пересекается с конусом по
кругу и разбивает конус на две части. Одна из частей представляет собой конус, а другая называется усеченным конусом.
Слайд 34
A
B
C
D
Усеченный конус – тело, полученное вращением прямоугольной трапеции
вокруг боковой стороны, содержащей прямой угол.
Слайд 35
По-гречески так назывался мяч, с которым играли дети.
Множество учёных геометров, да и простых людей, интересовались такой
фигурой как шар и его «оболочкой», носящей название сфера. Удивительно, но шар является единственным телом, обладающим большей площадью поверхности при объёме, равном объёму других сравниваемых тел, таких как куб, призма или прочие всевозможные многогранники. С шарами мы имеем дело ежедневно. К примеру, почти каждый человек пользуется шариковый ручкой в конец стержня которой вмонтирован металлический шар, вращающийся под действием сил трения между ним и бумагой и в процессе поворота на своей поверхности шар «выносит» очередную порцию чернил.Сфера и шар.
Слайд 36
A
B
O
Сфера – тело, полученное вращением окружности вокруг диаметра.
Шар
– тело, ограниченное сферой.
Слайд 38 Все касательные к сфере, проведенные из одной внешней
точки, равны между собой.
Проведем из внешней точки S
касательные к сфере SA, SB, SC. Точки их прикосновения A, B, C соединим с центром сферы О. Прямоугольные треугольники AOS, BOS, COS имеют общую гипотенузу SO и равные катеты ОА = ОВ = ОС, а потому они равны между собой. Следовательно, SA=SB=SC.A
O
B
C
S
Свойство касательной плоскости к сфере.
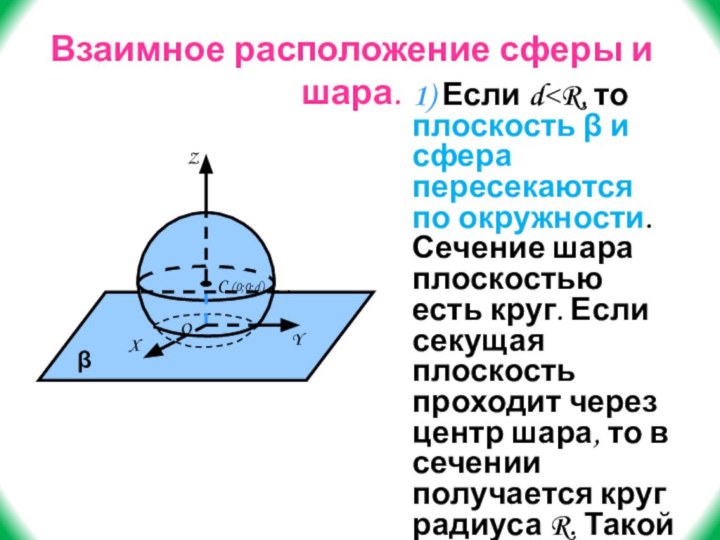
Слайд 39 1) Если d
пересекаются по окружности. Сечение шара плоскостью есть круг. Если
секущая плоскость проходит через центр шара, то в сечении получается круг радиуса R. Такой круг называется большим кругом шара.Взаимное расположение сферы и шара.
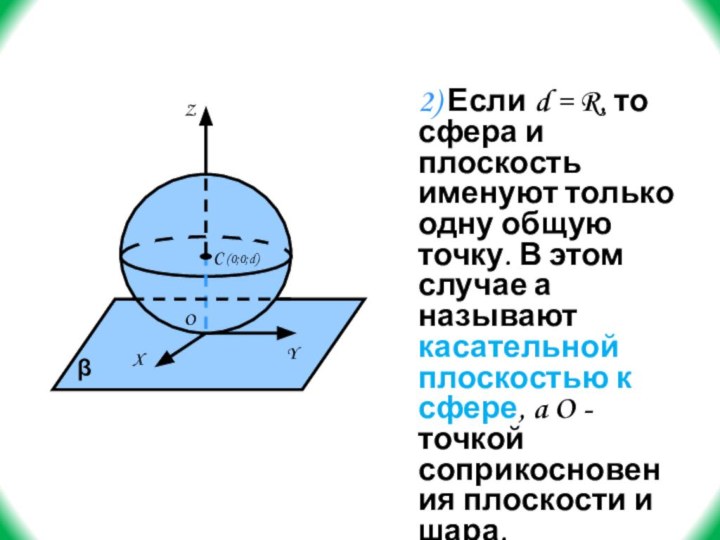
Слайд 40 2) Если d = R, то сфера и
плоскость именуют только одну общую точку. В этом случае
а называют касательной плоскостью к сфере, a O - точкой соприкосновения плоскости и шара.Слайд 42 Сферическая тригонометрия - область математики в которой
изучаются зависимости между сторонами и углами сферических треугольников (т.е.
треугольников на поверхности сферы), образующихся при пересечении трёх больших кругов. Сферическая тригонометрия тесно связана со сферической астрономией.Сферические функции (шаровые) – специальные функции, применяемые для изучения физических явлений в пространственных областях, ограниченных сферическими поверхностями.
Науки, связанные со сферами.
Слайд 43 Сферическая астрономия – раздел астрономии, разрабатывающий математические
методы решения задач, связанных с изучением видимого расположения и
движения космических тел (звезд, Солнца, планет, искусственных спутников Земли и др.) на небесной сфере, в частности разработка теоретических основ счета времени.Сферическая геометрия – область математики, в которой изучаются геометрические фигуры на сфере. Развитие сферической геометрии в античной древности было связано с задачами сферической астрономии.
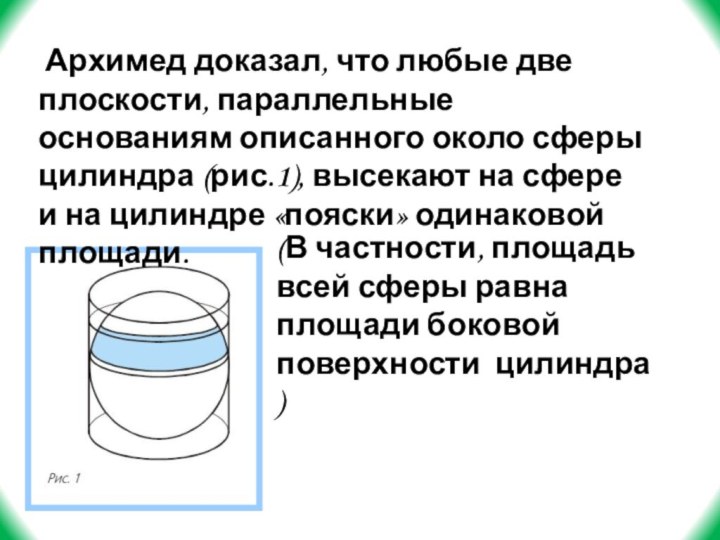
Слайд 44 Архимед доказал, что любые две плоскости, параллельные
основаниям описанного около сферы цилиндра (рис.1), высекают на сфере
и на цилиндре «пояски» одинаковой площади.(В частности, площадь всей сферы равна площади боковой поверхности цилиндра )
Слайд 45 Трехгранный угол с вершиной в центре сферы высекает
на ней сферический треугольник (рис.2). Стороны сферического треугольника –
дуги больших кругов.Поскольку касательные m и l к сфере перпендикулярны радиусу ОА, то величины А, В и С углов сферического треугольника равны величинам соответствующих двухгранных углов трехгранного угла.
Слайд 46 Как расположить на сфере n точек, чтобы наименьшее
из всех расстояний между ними было как можно больше?
Эта задача не решена до сих пор. Оптимальные расположения при n=2, 3, …, 9 показаны на рисунках, где линиями соединены те точки, расстояния между которыми равны наименьшему из расстояний между рассматриваемыми n точками.При n > 9 решение известно для n=12 (вершины икосаэдра) и n=24 (вершины полуправильного 38-гранника (полуправильный многоугольник- многоугольник, получаемый при проектировании правильного многоугольника на какую-либо плоскость), ограниченного 32 равносторонними треугольниками и 6 квадратами; в каждой вершине не сходятся 4 треугольника и 1 квадрат).
