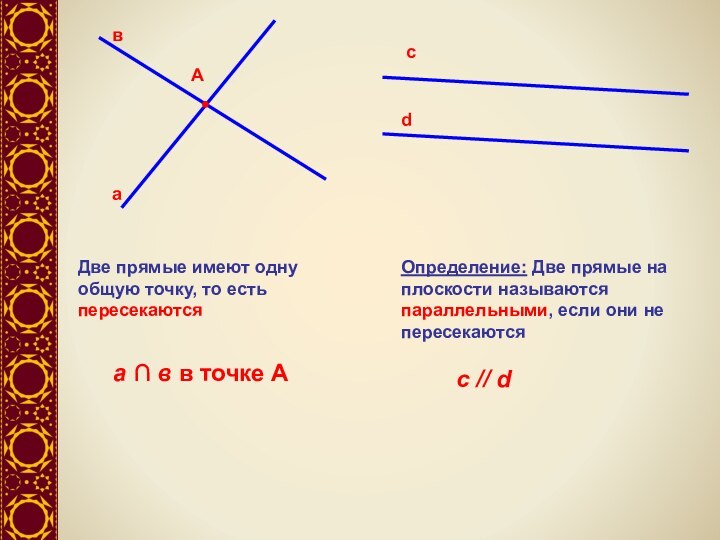
пересекаются
а ∩ в в точке А
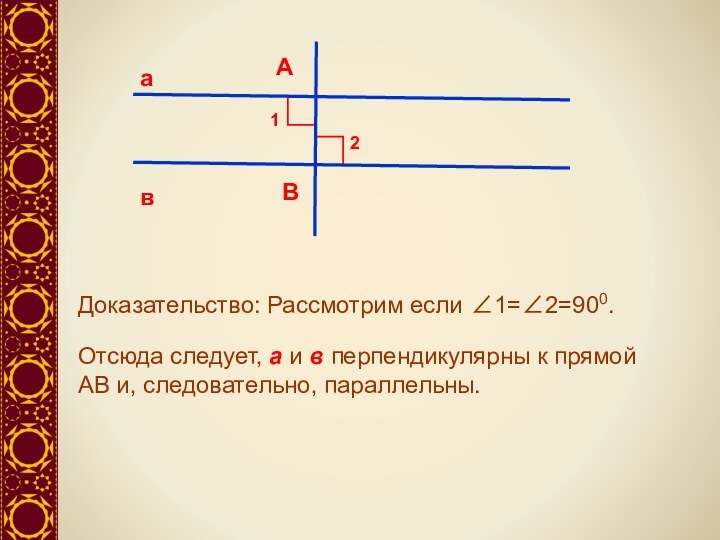
Определение: Две прямые на
плоскости называются параллельными, если они не пересекаютсяс // d
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

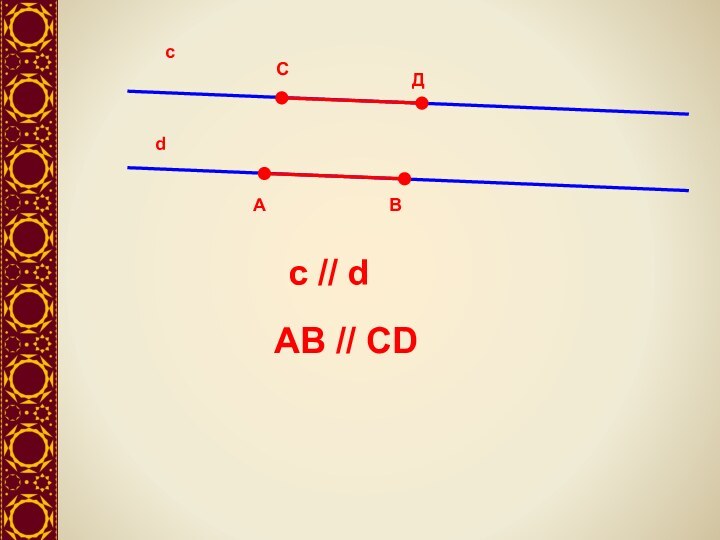




с // d
Соответственные углы – 1 и 5; 2 и 6; 4 и 8; 3 и 7.
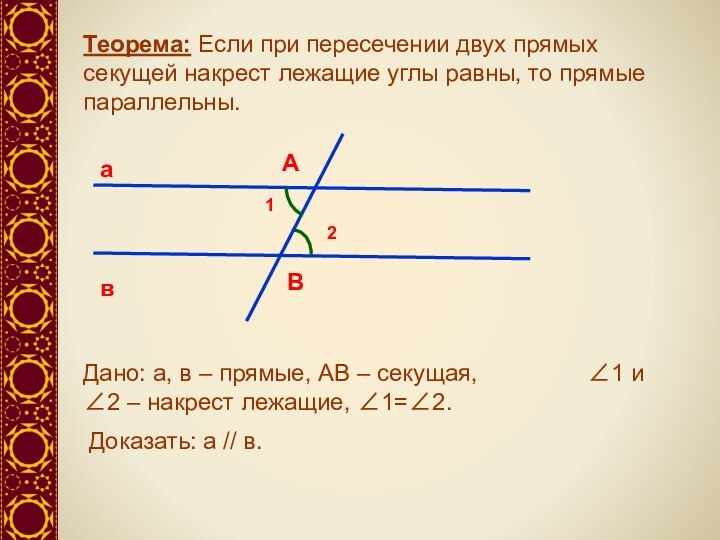
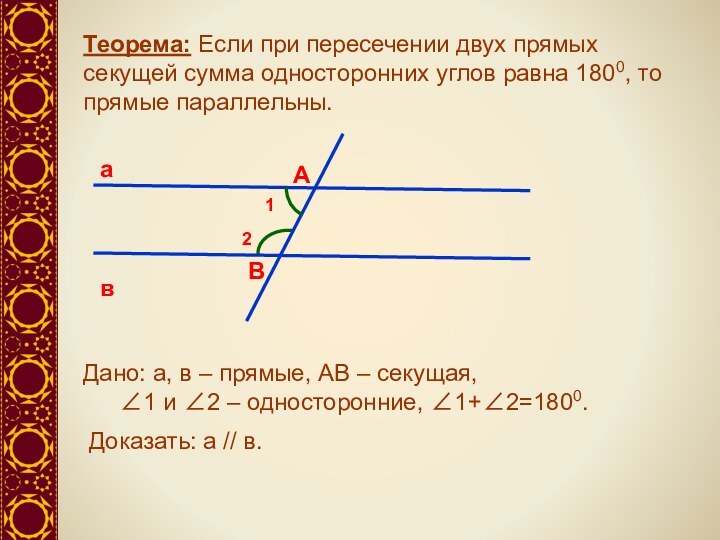
Доказать: а // в.
Доказать: а // в.
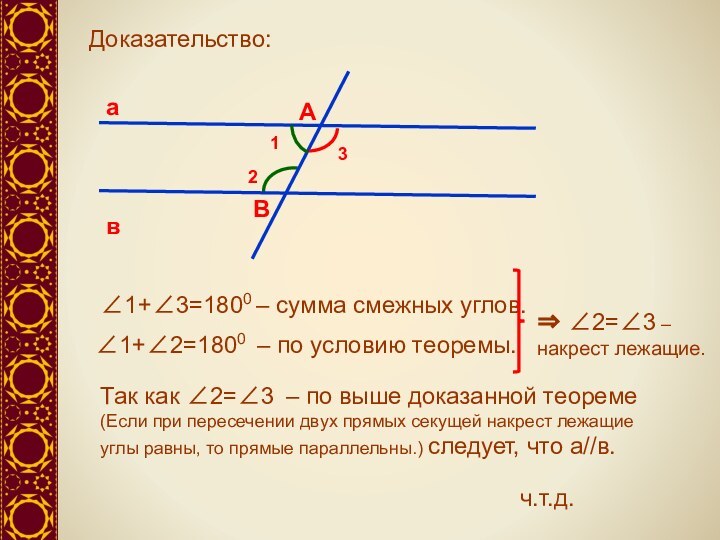
∠1+∠2=1800 – по условию теоремы.
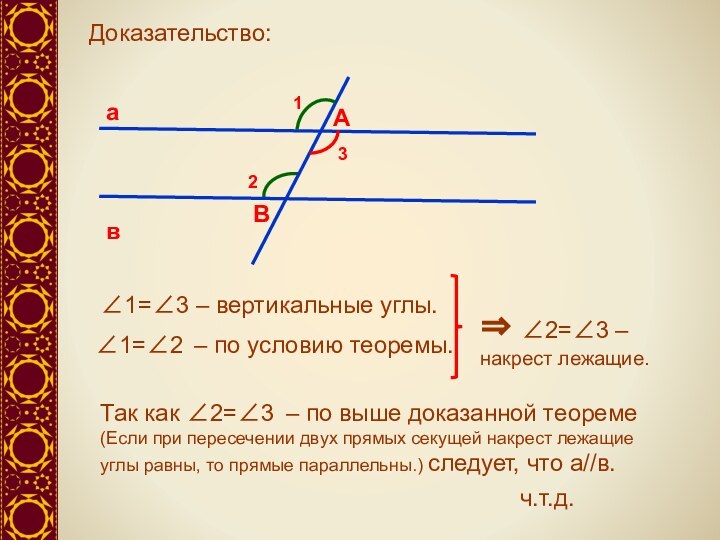
⇒ ∠2=∠3 – накрест лежащие.
ч.т.д.
Доказать: а // в.