Слайд 2
Содержание
Введение.
Основная цель.
Начальные геометрические сведения.
Точки, прямые, отрезки.
Луч и угол.
Градусная
мера угла.
Смежные и вертикальные углы
Перпендикулярные прямые.
Вопросы.
Треугольники.
Медианы, биссектрисы и высоты треугольника.
Первый признак равенства треугольников
Второй и третий признаки равенства
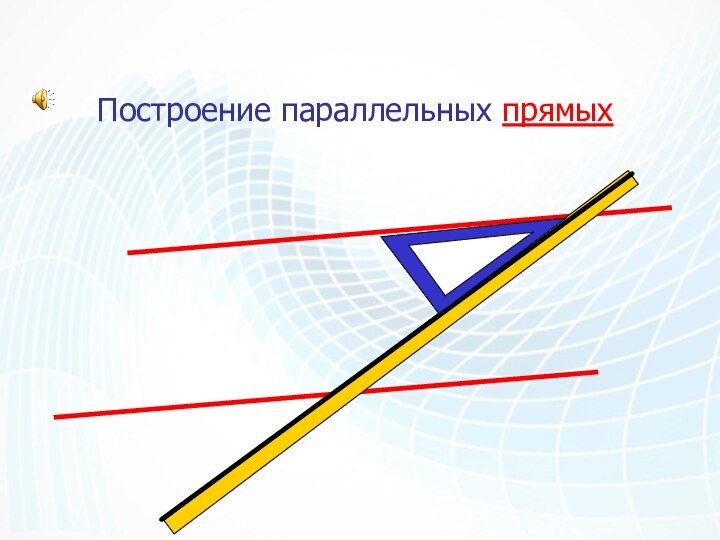
Задачи на построение.
Вопросы.
Слайд 3
Содержание
Параллельные прямые.
Признаки параллельности прямых
Аксиома параллельных прямых.
Вопросы.
Выводы.
Литература.
Слайд 4
Введение:
Геометрия наука, занимающаяся изучением геометрических фигур. На уроках
геометрии мы познакомимся с новыми фигурами и со многими
важными и интересными свойствами уже известных вам фигур. Вы узнаете о том, как используются свойства геометрических фигур в практической деятельности. Материал данной презентации посвящен введению основных геометрических понятий. Наглядное представление о простейших геометрических фигурах и их свойствах, признаки равенства треугольников, признаки параллельности прямых.
Слайд 5
Основная цель:
Научить использовать геометрический язык для описания предметов
окружающего мира. Систематизировать знания учащихся об основных простейших геометрических
фигурах, ввести понятия равенство отрезков. Распознавать на чертежах и моделях геометрические фигуры (отрезки, прямые, лучи, углы).
Расширить знания учащихся о треугольнике.
Дать систематические сведения о параллельности прямых, ввести аксиому параллельных прямых.
Введение терминологии. Наглядное изображение планиметрических фигур и простейших геометрических конфигураций. Показать измерительные инструменты. Познакомить с единицами измерения.
Слайд 6
Простейшие
геометрические фигуры
O
O
A
B
K
P
Слайд 7
«Я думаю, что никогда до настоящего времени
мы
не жили в такой геометрический период. Всё вокруг –
геометрия»
Ле Корбюзье
Слайд 9
Точки, прямые, отрезки
«Точка» в русском языке – конец
заточенного гусиного пера.
A
C
B
D
«Точка есть то,
что не имеет частей»
Евклид
Слайд 10
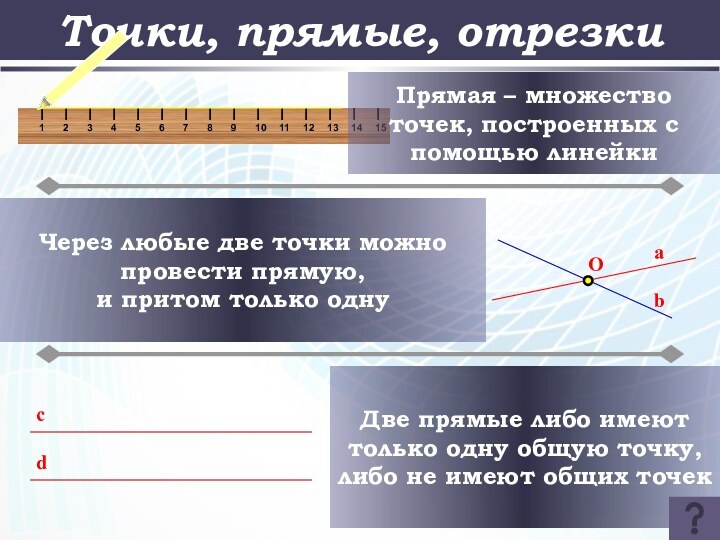
Точки, прямые, отрезки
Прямая – множество точек, построенных с
помощью линейки
Через любые две точки можно провести прямую,
и
притом только одну
c
d
Две прямые либо имеют только одну общую точку, либо не имеют общих точек
Слайд 11
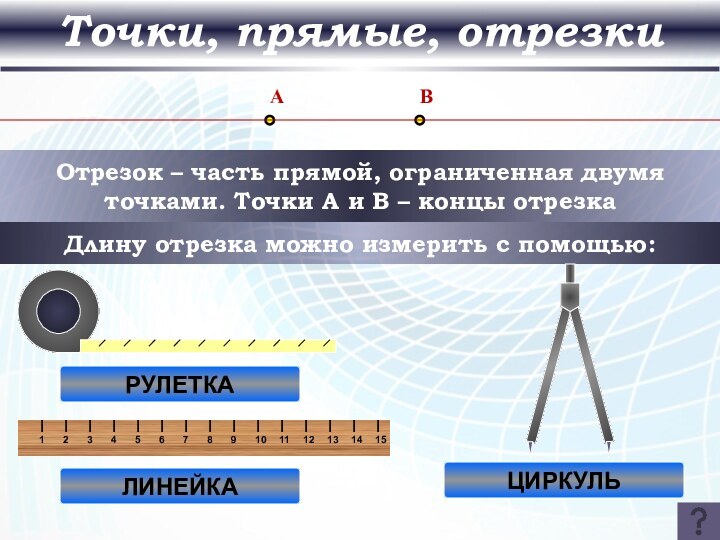
Точки, прямые, отрезки
Отрезок – часть прямой, ограниченная двумя
точками. Точки A и B – концы отрезка
A
B
Длину отрезка
можно измерить с помощью:
РУЛЕТКА
ЛИНЕЙКА
ЦИРКУЛЬ
Слайд 12
Точки, прямые, отрезки
Единицы измерения длины:
Слайд 13
Точки, прямые, отрезки
A
B
M
N
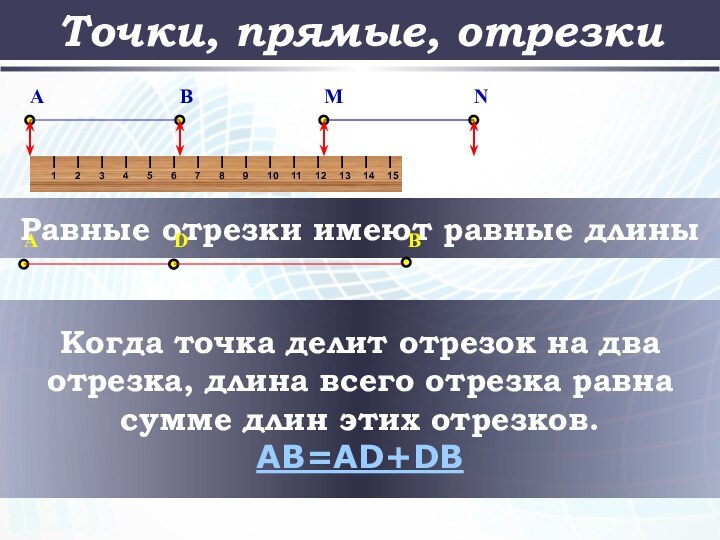
Равные отрезки имеют равные длины
A
D
B
Когда точка
делит отрезок на два отрезка, длина всего отрезка равна
сумме длин этих отрезков.
AB=AD+DB
Слайд 14
Луч и угол
O
Точка разделяет прямую на две части,
каждая из которых называется лучом, исходящим из точки O
Точка
O называется началом каждого из лучей
Луч обозначают либо малой латинской буквой…
…либо двумя большими латинскими буквами, первая из которых обозначает начало луча,
а вторая – какую-нибудь точку на луче, например:
Луч h
Луч OA
Слайд 15
Луч и угол
Угол – это геометрическая фигура, которая
состоит из точки и двух лучей, исходящих из этой
точки.
O
A
B
k
h
Угол
Угол называется развернутым, если обе его стороны лежат на одной прямой.
p
q
С
Развернутый угол
Слайд 16
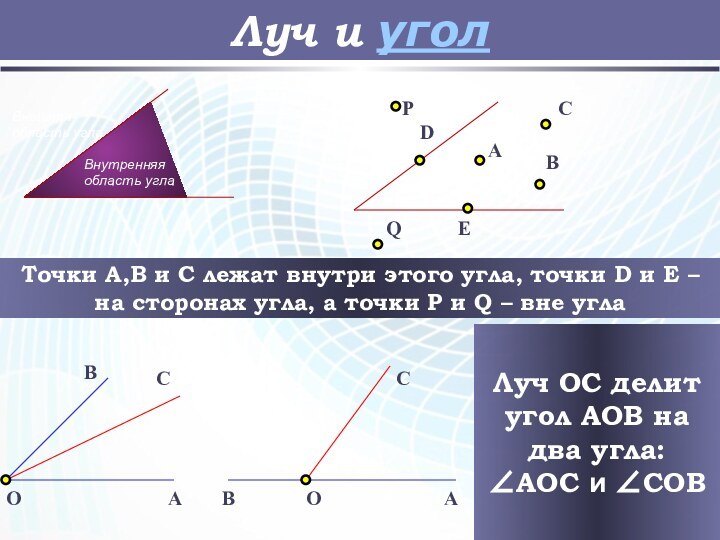
Луч и угол
Точки A,B и C лежат внутри
этого угла, точки D и E – на сторонах
угла, а точки P и Q – вне угла
Луч OC делит угол AOB на два угла:
∠AOC и ∠COB
Слайд 17
Градусная мера угла
Всего 360 частей.
1 часть – это
1 градус.
1/60 часть градуса называется минутой, обозначается знаком «′»
1/60
часть минуты называется секундой, обозначается знаком «″»
Равные углы имеют равные градусные меры
Слайд 18
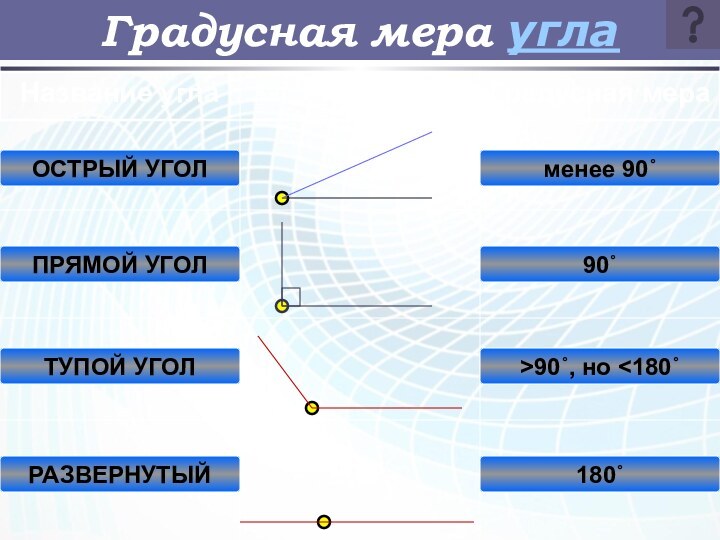
Градусная мера угла
ОСТРЫЙ УГОЛ
ПРЯМОЙ УГОЛ
ТУПОЙ УГОЛ
РАЗВЕРНУТЫЙ
менее 90˚
90˚
>90˚, но
Слайд 19
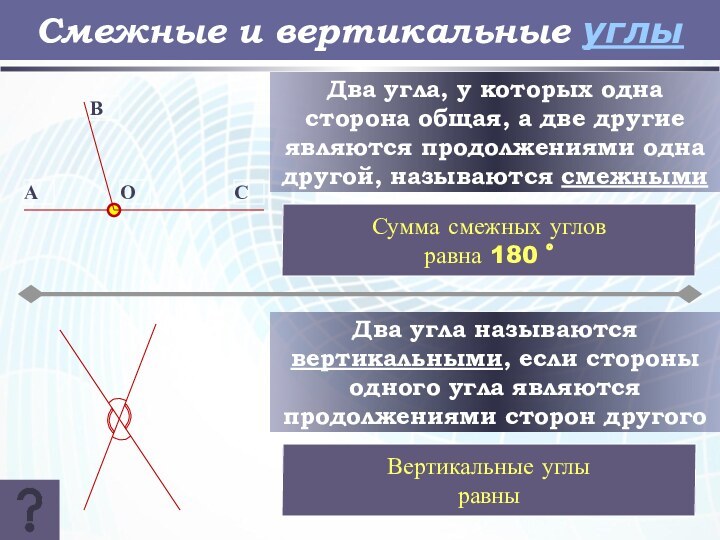
Смежные и вертикальные углы
Два угла, у которых одна
сторона общая, а две другие являются продолжениями одна другой,
называются смежными
Сумма смежных углов
равна 180 ˚
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого
Вертикальные углы
равны
Слайд 20
Перпендикулярные прямые.
B
D
C
A
1
Две пересекающиеся прямые называются перпендикулярными (или взаимно
перпендикулярными), если они образуют четыре прямых угла.
Две прямые, перпендикулярные
к третьей, не пересекаются.
Слайд 21
Вопросы:
Сколько прямых можно провести через две точки?
Что такое
отрезок?
Какие вы знаете единицы измерения?
Что такое луч?
Какая фигура называется
углом?
Какой луч называется биссектрисой угла?
Какие фигуры называются равными?
Какими инструментами пользуются для измерения расстояния?
Что такое градусная мера угла?
Какой угол называется острым? Прямым? Тупым?
Какие углы называются вертикальными? Смежными?
Какие прямые называются перпендикулярными?
Слайд 22
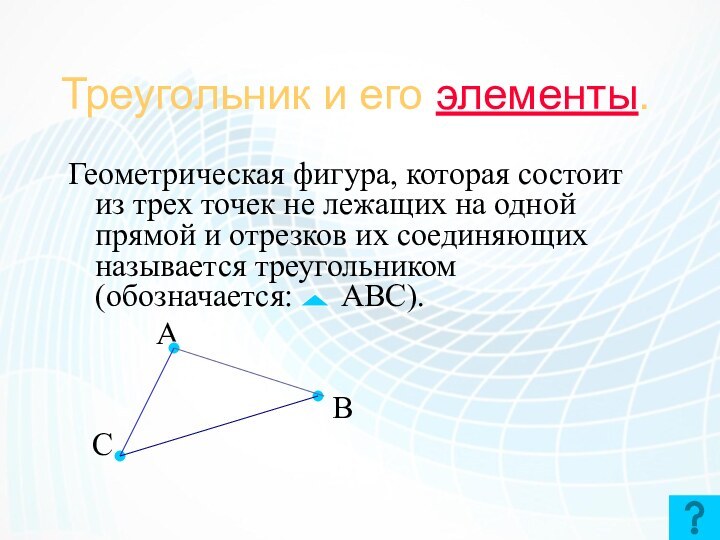
Треугольник и его элементы.
Геометрическая фигура, которая состоит из
трех точек не лежащих на одной прямой и отрезков
их соединяющих называется треугольником (обозначается: АВС).
А
В
С
Слайд 23
Треугольником также называется часть плоскости ограниченная отрезками АВ,
ВС, АС.
А
С
В
А, В, С – вершины.
АВ, ВС, СА-стороны.
<АВС, <ВСА, <САВ-углы треугольника,(<А,< В, <С или α, β, γ ).
Углы треугольника.
А
<А, <В, <С- внутренние углы
<А противолежит стороне СВ…
<АВD-внешний угол;
Теорема: внешний угол равен
сумме внутренних углов не
смежных с ним.
С В D
Слайд 25
Треугольник с вершинами A, B, C, и сторонами
AB, BC, CA
A
C
B
A
C
B
A1
C1
B1
Сумма длин трех сторон треугольника называется его
периметром
Каждый из этих треугольников можно наложить на другой так, что они полностью совместятся, т.е. попарно совместятся их вершины и стороны
Слайд 26
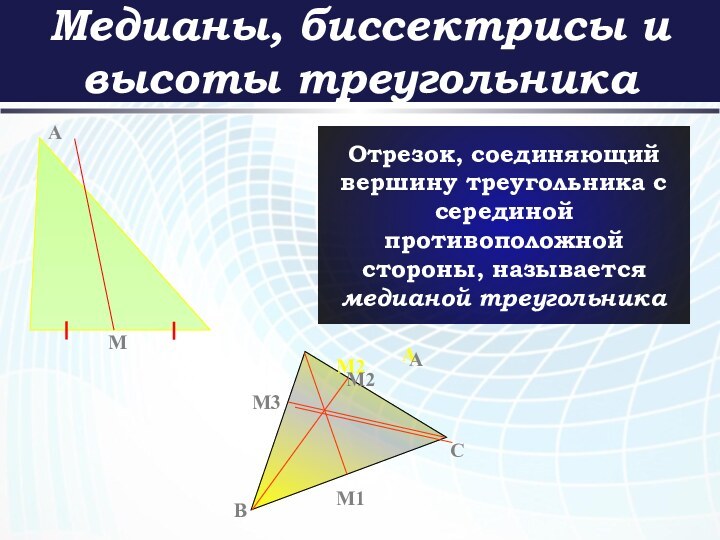
Медианы, биссектрисы и высоты треугольника
a
A
Из точки, не лежащей
на прямой, можно провести перпендикуляр к этой прямой, и
притом только один
a
H
A
Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник
Слайд 27
Медианы, биссектрисы и высоты треугольника
A
M
Отрезок, соединяющий вершину треугольника
с серединой противоположной стороны, называется медианой треугольника
A
C
M2
B
M1
M3
A
M2
Слайд 28
Медианы, биссектрисы и высоты треугольника
A
A1
B
C
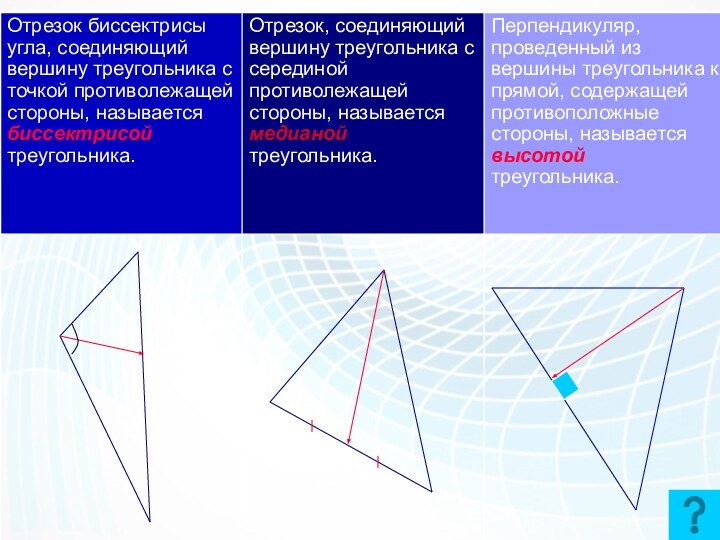
Отрезок биссектрисы угла треугольника,
соединяющий вершину треугольника с точкой противоположной стороны, называется Биссектрисой
треугольника
A
B
H
C
Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника
Слайд 30
Равных сторон нет –
(разносторонние)
Две равные стороны
–
(равнобедренные)
Все стороны равны –
(равносторонние)
Слайд 31
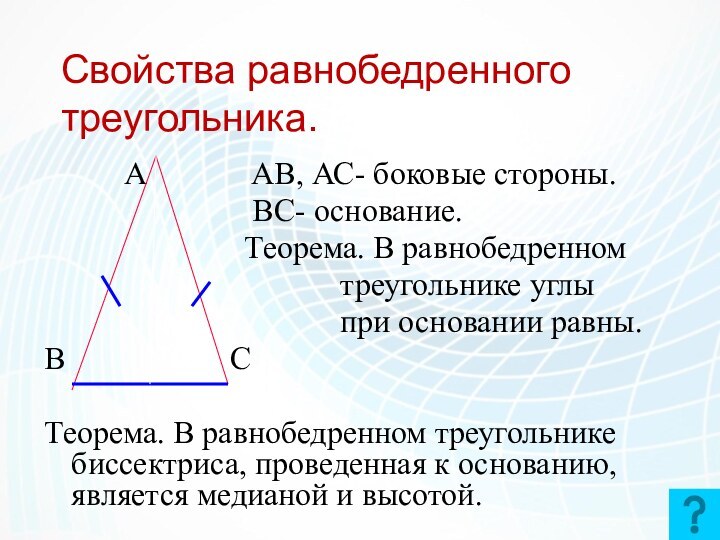
Свойства равнобедренного треугольника.
А
АВ, АС- боковые
стороны.
ВС- основание.
Теорема. В равнобедренном
треугольнике углы
при основании равны.
В С
Теорема. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Слайд 32
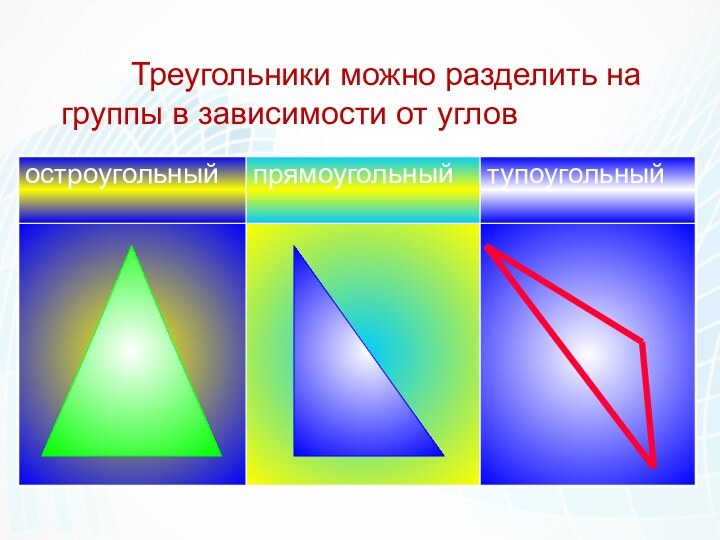
Треугольники можно разделить на
группы в зависимости от углов
Слайд 33
Первый признак равенства треугольника
Слайд 34
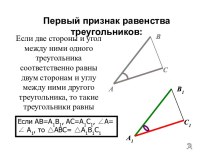
Первый признак равенства треугольника
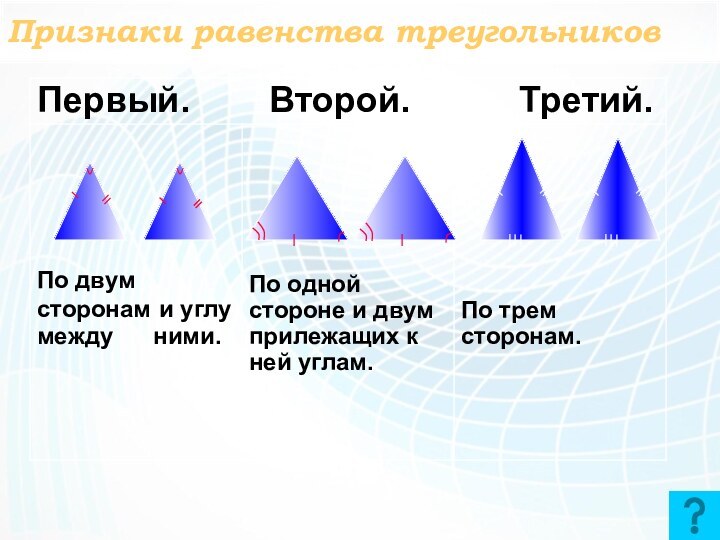
Если две стороны и угол
между ними одного треугольника соответственно равны двум сторонам и
углу между ними другого треугольника, то такие треугольники равны
Слайд 35
Второй признак равенства треугольников
Если сторона и два прилежащих
к ней угла одного треугольника соответственно равны стороне и
двум прилежащим к ней углам другого треугольника, то такие треугольники равны
Слайд 36
Третий признак равенства треугольников
Если три стороны одного треугольника
соответственно равны трем сторонам другого треугольника, то такие треугольники
равны
Слайд 37
Признаки равенства треугольников
Слайд 39
Вопросы:
Какая фигура называется треугольником?
Какой отрезок называется высотойКакой отрезок
называется высотой, медианойКакой отрезок называется высотой, медианой, биссектрисой?
Какими замечательными
свойствами обладают медианы, высоты, биссектрисы?
-Что общего между биссектрисой , высотой и медианой?
Какой треугольник называется равностороннимКакой треугольник называется равносторонним, равнобедренным?
Сформулируйте свойства равнобедренного треугольника?
Сформулируйте первыйСформулируйте первый, второйСформулируйте первый, второй, третий признаки равенства треугольников?
Слайд 41
Определение
Две прямые на плоскости называются параллельными, если
они не пересекаются.
a
b
Слайд 42
Секущая прямая
Прямая называется секущей, если она пересекает две
параллельные прямые в двух точках.
c
a
b
Слайд 44
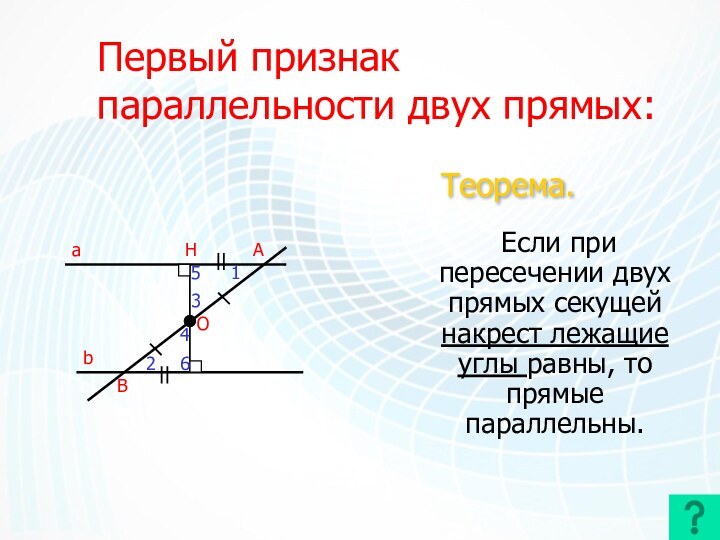
Первый признак параллельности двух прямых:
Если при
пересечении двух прямых секущей накрест лежащие углы равны, то
прямые параллельны.
Теорема.
Слайд 45
Второй признак параллельности двух прямых:
Теорема.
Если при пересечении двух
прямых секущей соответственные углы равны, то прямые параллельны.
1
2
3
1
=
2
=
3
Слайд 46
Третий признак параллельности двух прямых:
Теорема.
Если при пересечении двух
прямых секущей сумма односторонних углов равна 180°, то прямые
параллельны.
Слайд 48
Аксиомы
Аксиома – утверждение, не требующее доказательств
Само слово «
аксиома » происходит от греческого «аксиос», что означает «ценный,
достойный». Древнегреческий ученый Евклид первым придумал аксиомы, которые были изложены в его знаменитом сочинении «Начала».
Слайд 49
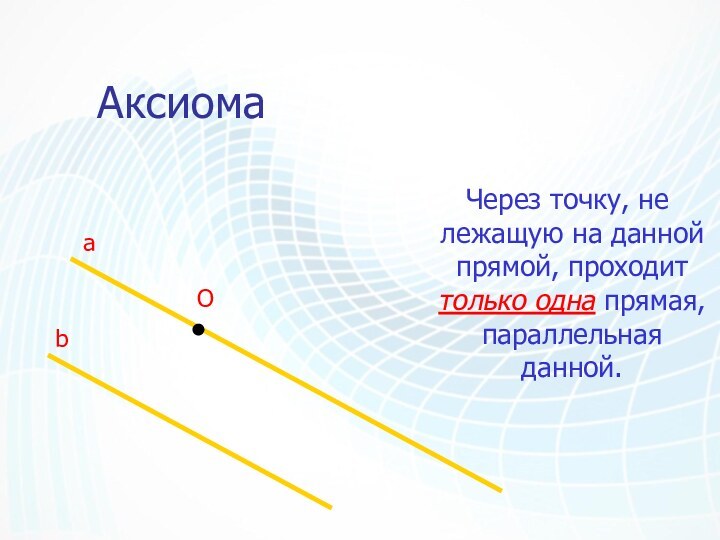
Аксиома
Через точку, не лежащую на данной прямой,
проходит только одна прямая, параллельная данной.
а
b
О
Слайд 50
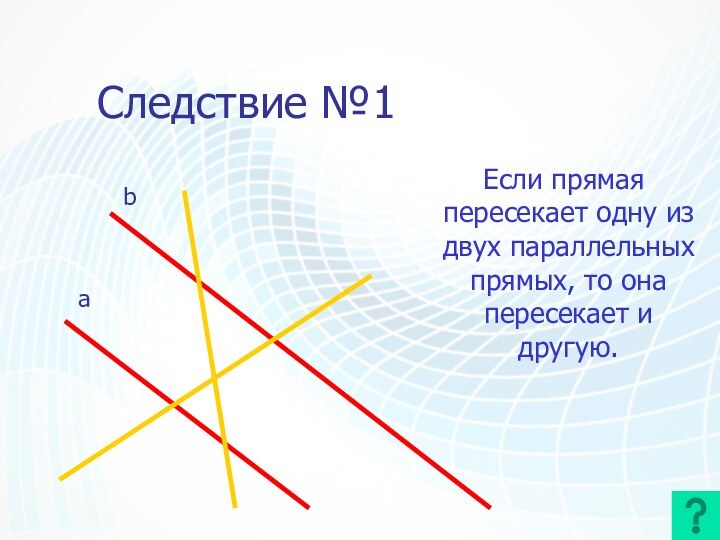
Следствие №1
Если прямая пересекает одну из двух
параллельных прямых, то она пересекает и другую.
a
b
Слайд 51
Следствие №2
Если две прямые параллельны третьей, то
они параллельны.
Слайд 52
«Если бы мне пришлось начать вновь своё обучение,
то я последовал бы совету Платона и принялся бы
сперва за математику».
Галилей Г.
Слайд 53
Вопросы:
Дайте определение параллельных прямых.
Что такое секущая?
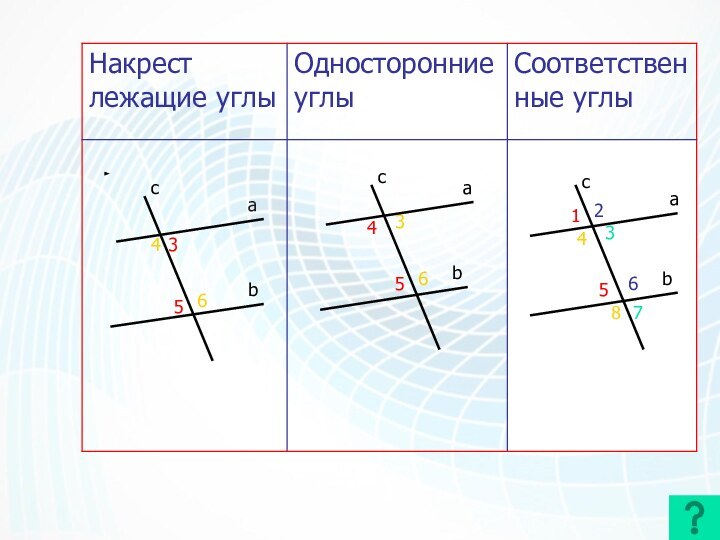
Какие углы называются
накрест лежащимиКакие углы называются накрест лежащими? одностороннимиКакие углы называются
накрест лежащими? односторонними? соответственными?
Сформулируйте первыйСформулируйте первый, второйСформулируйте первый, второй, третий признаки параллельности параллельных прямых.
Какие утверждения называются аксиомами?
Сформулируйте первоеСформулируйте первое и второе следствие о параллельных прямых.
Слайд 54
Выводы:
Данная презентация поможет ученикам 7-х классов познакомиться с
геометрией. Представить себе, что такое точка, прямая, отрезок, луч,
угол, треугольник, параллельные прямые, как они могут быть расположены относительно друг друга. А также решать задачи на вычисление геометрических величин (длин, углов), изображать указанные геометрические фигуры.