,
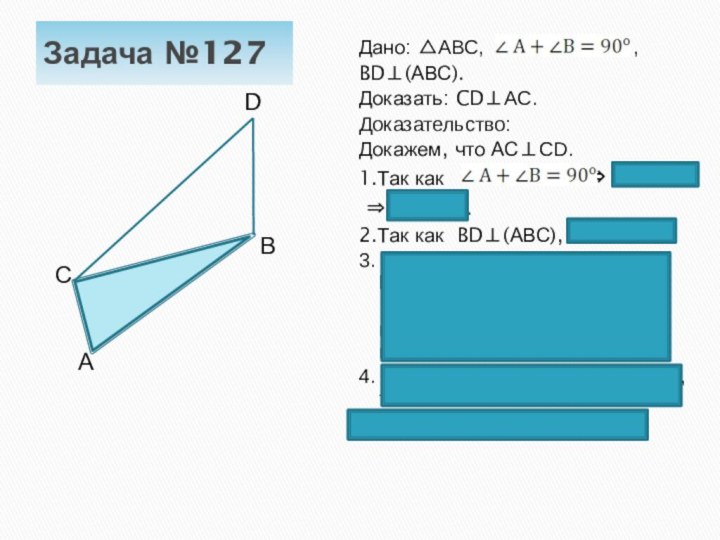
BD⊥(АВС).
Доказать: CD⊥АС.
Доказательство:
Докажем, что АС⊥CD.
1.Так как ⇒
⇒ АС⊥ВС.
2.Так как BD⊥(АВС), то ВD⊥АС.
3. Так как АС⊥ВС, АС⊥ВD, ВС∩ВD=В, ВС,ВD⊂(ВСD), то
АС⊥(ВСD)(по признаку перпендикулярности прямой и плоскости)
4. Так как CD⊂(ВСD) и АС⊥(ВСD), то АС⊥DС.
Что и требовалось доказать.
D
В
С
А