- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии на тему Комбинации многогранников в прикладных задачах (10 класс)
Содержание
- 2. Математика владеет не только истинной, но и
- 3. Тема «Многогранники» - одна из основных тем
- 4. Сведения из истории о правильных многогранниках. Одно
- 5. Начиная с 7 века до нашей эры,
- 6. Существование только пяти правильных многогранников относили к
- 10. ИТАК, ПРОБЛЕМА.В небольшой квартире очень мало места,
- 11. Решение поставленной проблемы.Итак, спец-предложение: какая – то
- 12. Общий вид изделия.
- 13. Практическая задача.Для того, чтобы производители смогли затратить
- 14. Геометрическая задача.В правильной усеченной пирамиде ABCDEFA1B1C1D1E1F1 проведено
- 15. Исходные данные.Дано:ABCDEFA1B1C1D1E1F1-правильная усеченная пирамида, A1B1C1D1E1F1A2B2C2D2E2F2-правильная призма, A1D1D2A2
- 16. Решение.1)Sполн.призмы =SA1B1C1D1E1F1A2B2C2D2E2F2= =Sбок+2SA1B1C1D1E1F12)Достроим усеченную пирамиду ABCDEFA1B1C1D1E1F1 до
- 17. 7) POA= POB=…= POF(т.к. PO-общая,
- 18. Чтобы найти площадь полной поверхности нашего изделия,
- 19. 10) Аналогично, как и в действии 9)а)
- 20. Скачать презентацию
- 21. Похожие презентации


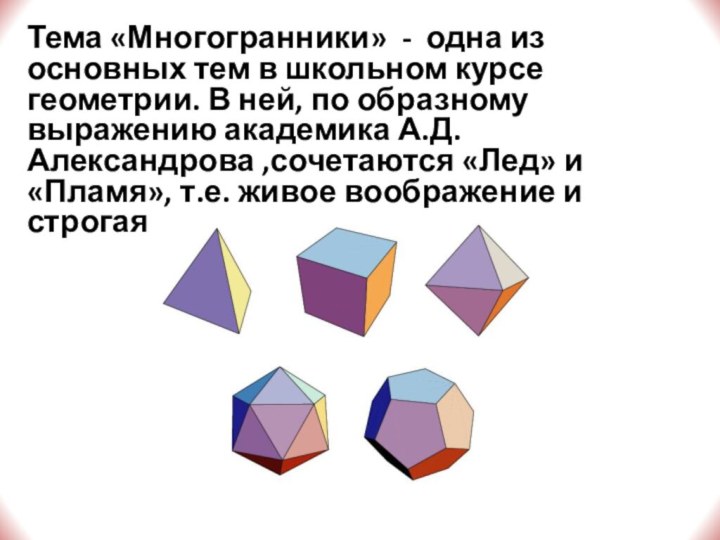







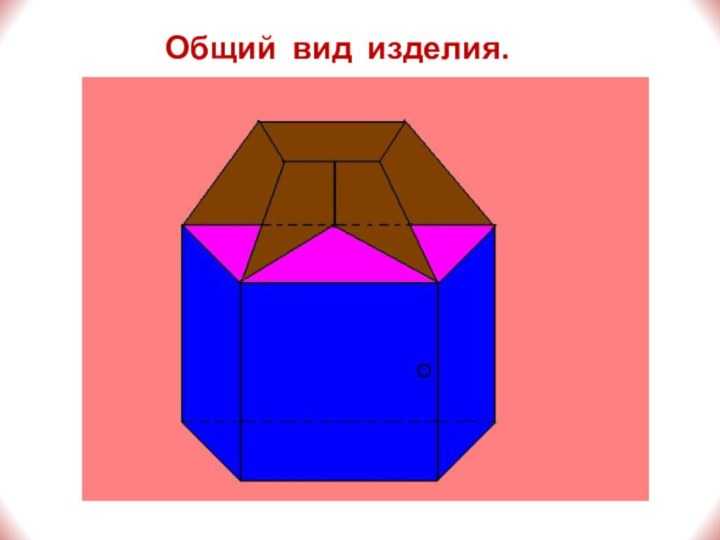


Слайд 3 Тема «Многогранники» - одна из основных тем в
школьном курсе геометрии. В ней, по образному выражению академика
А.Д. Александрова ,сочетаются «Лед» и «Пламя», т.е. живое воображение и строгая логика.
Слайд 4
Сведения из истории о правильных многогранниках.
Одно из
древнейших упоминаний о правильных многогранниках находится в трактате Платона
(427-347 до н.э.) «Тимаус». Поэтому правильные многогранники также называются платоновыми телами (хотя известны они были задолго до Платона). Каждый из правильных многогранников, а всего их пять, Платон ассоциировал с четырьмя «земными» элементами: земля (куб), вода (икосаэдр), огонь (тетраэдр), воздух (октаэдр), а также с «неземным» элементом- вселенной (додекаэдр). Знаменитый математик и астроном Кеплер построил модель Солнечной системы как ряд последовательно вписанных и описанных правильных многогранников и сфер.Слайд 5 Начиная с 7 века до нашей эры, в
Древней Греции создаются философские школы , в которых происходит
постепенный переход от практической к философской геометрии. Большое значение в этих школах приобретают рассуждения, с помощью которых удалось получать новые геометрические свойства. Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора. Отличительным знаком пифагорейцев была пентаграмма, на языке математики- это правильный невыпуклый или звездчатый пятиугольник. Пентаграмме присваивалось способность защищать человека от злых духов.(580 – 500 до н.э.)
Слайд 6 Существование только пяти правильных многогранников относили к строению
материи и Вселенной. Пифагорейцы, а затем и Платон, полагали,
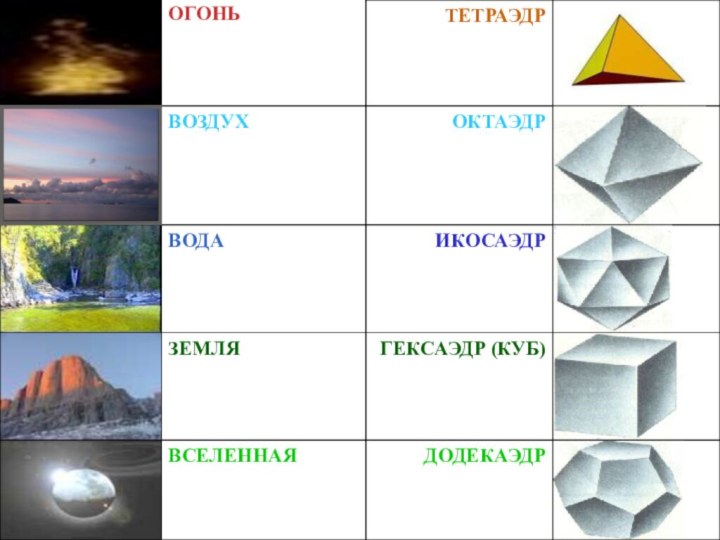
что материя состоит из четырех основных элементов: огня, земли, воздуха и воды. Согласно их мнению, атомы основных элементов должны иметь форму различных Платоновых тел.ОГОНЬ-ТЕТРАЭДР.
ВОЗДУХ-ОКТАЭДР.
ВОДА-ИКОСАЭДР.
ЗЕМЛЯ-ГЕКСАЭДР (КУБ).
ВСЕЛЕННАЯ-ДОДЕКАЭДР.
Платон
Слайд 10
ИТАК, ПРОБЛЕМА.
В небольшой квартире очень мало места, некуда
складывать книги, различные старые вещи, но, в то же
время, громоздкие полки сужают пространство и не всегда вписываются в интерьер комнаты. Мелкие безделушки и статуэтки разбросаны по углам, но, к счастью, можно найти компромиссное решение!
Слайд 11
Решение поставленной проблемы.
Итак, спец-предложение: какая – то гипотетическая
компания по разработке интерьера и новой мебели выпустила компактную
полку-тумбочку, которая не займет слишком много места в квартире и будет необычным дополнением к образу комнаты. В ней поместятся некоторые книги, журналы и ненужные вещи, которые жалко выкинуть, также в верхней ее части можно расположить статуэтки, рамки для фотографий и многое другое.
Слайд 13
Практическая задача.
Для того, чтобы производители смогли затратить необходимое
количество материала, который потребуется для изготовления нашей полки -
тумбочки, нам необходимо высчитать площадь ее полной поверхности.
Слайд 14
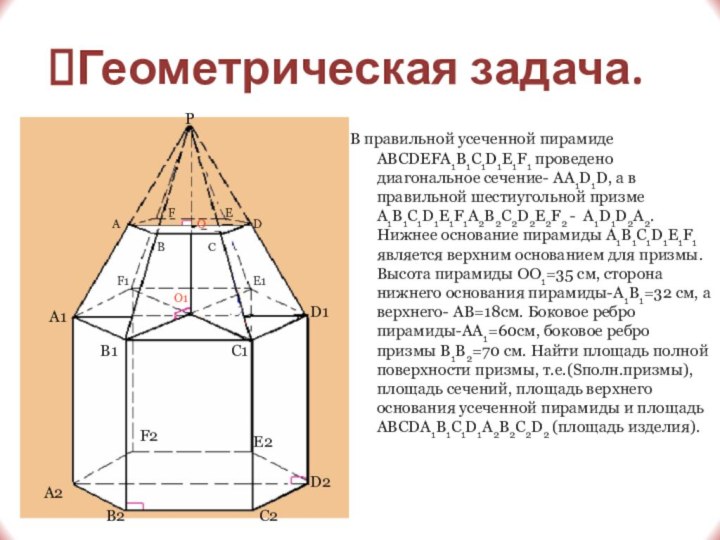
Геометрическая задача.
В правильной усеченной пирамиде ABCDEFA1B1C1D1E1F1 проведено диагональное
сечение- AA1D1D, а в правильной шестиугольной призме A1B1C1D1E1F1A2B2C2D2E2F2 -
A1D1D2A2. Нижнее основание пирамиды A1B1C1D1E1F1 является верхним основанием для призмы. Высота пирамиды OO1=35 см, сторона нижнего основания пирамиды-A1B1=32 см, а верхнего- AB=18см. Боковое ребро пирамиды-AA1=60см, боковое ребро призмы B1B2=70 см. Найти площадь полной поверхности призмы, т.е.(Sполн.призмы), площадь сечений, площадь верхнего основания усеченной пирамиды и площадь ABCDA1B1C1D1A2B2C2D2 (площадь изделия).
Слайд 15
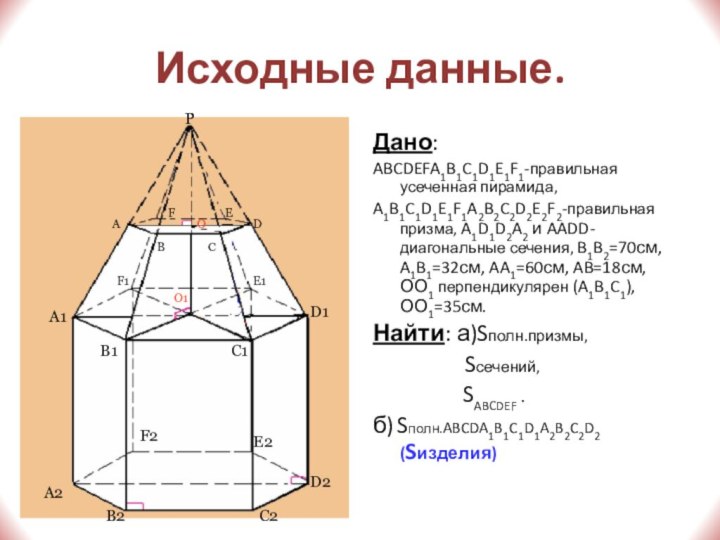
Исходные данные.
Дано:
ABCDEFA1B1C1D1E1F1-правильная усеченная пирамида,
A1B1C1D1E1F1A2B2C2D2E2F2-правильная призма, A1D1D2A2 и
AADD-диагональные сечения, B1B2=70см, A1B1=32см, AA1=60см, AB=18см, ОО1 перпендикулярен (A1B1C1),
ОО1=35см.Найти: а)Sполн.призмы,
Sсечений,
SABCDEF .
б) Sполн.ABCDA1B1C1D1A2B2C2D2 (Sизделия)
Слайд 16
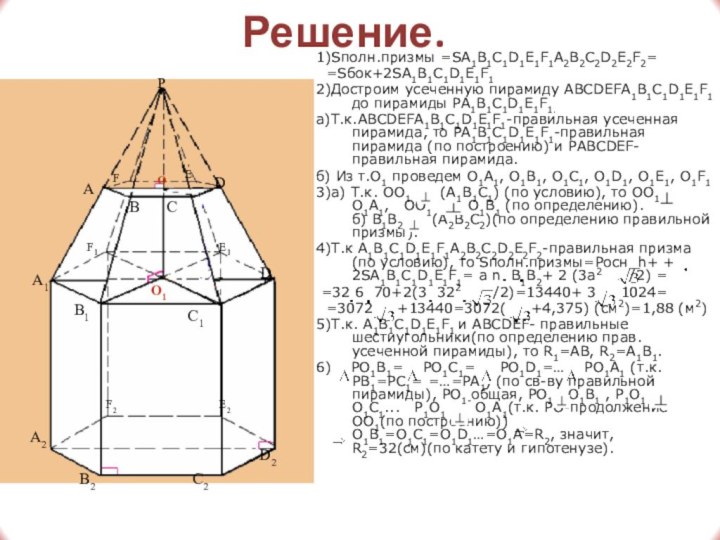
Решение.
1)Sполн.призмы =SA1B1C1D1E1F1A2B2C2D2E2F2=
=Sбок+2SA1B1C1D1E1F1
2)Достроим усеченную пирамиду ABCDEFA1B1C1D1E1F1 до пирамиды
PA1B1C1D1E1F1.
а)Т.к.ABCDEFA1B1C1D1E1F1-правильная усеченная пирамида, то PA1B1C1D1E1F1-правильная пирамида (по построению) и
PABCDEF-правильная пирамида.б) Из т.O1 проведем O1A1, O1B1, O1C1, O1D1, O1E1, O1F1
3)а) Т.к. OO1 (A1B1C1) (по условию), то OO1 O1A1, OO1 O1B1 (по определению). б) B1B2 (A2B2C2)(по определению правильной призмы).
4)Т.к A1B1C1D1E1F1A2B2C2D2E2F2-правильная призма(по условию), то Sполн.призмы=Pосн h+ + 2SA1B1C1D1E1F1= a n B1B2+ 2 (3a2 /2) =
=32 6 70+2(3 322 /2)=13440+ 3 1024=
=3072 +13440=3072( +4,375) (см2)=1,88 (м2)
5)Т.к. A1B1C1D1E1F1 и ABCDEF- правильные шестиугольники(по определению прав. усеченной пирамиды), то R1=AB, R2=A1B1.
6) PO1B1= PO1C1= PO1D1=… PO1A1 (т.к. PB1=PC1= =…=PA1, (по св-ву правильной пирамиды), PO1-общая, PO1 O1В1 , P1O1 O1C1... P1O1 O1A1(т.к. PO-продолжение OO1(по построению)) O1B1=O1C1=O1D1…=O1A=R2, значит, R2=32(см)(по катету и гипотенузе).
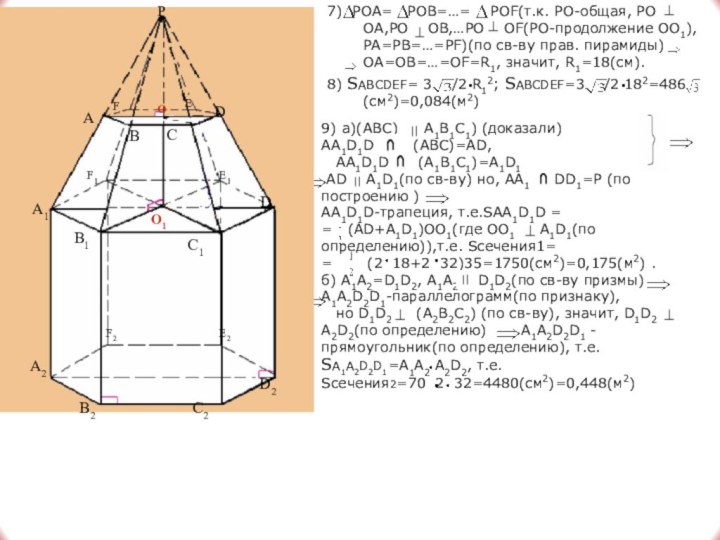
Слайд 17 7) POA= POB=…= POF(т.к. PO-общая, PO
OA,PO OB,…PO OF(PO-продолжение OO1),
PA=PB=…=PF)(по св-ву прав. пирамиды) OA=OB=…=OF=R1, значит, R1=18(см).8) SABCDEF= 3 /2 R12; SABCDEF=3 /2 182=486 (см2)=0,084(м2)
9) а)(ABC) (A1B1C1) (доказали) AA1D1D (ABC)=AD,
AA1D1D (A1B1C1)=A1D1
AD A1D1(по св-ву) но, AA1 DD1=P (по построению ) AA1D1D-трапеция, т.е.SAA1D1D =
= (AD+A1D1)OO1(где OO1 A1D1(по определению)),т.е. Sсечения1= = (2 18+2 32)35=1750(см2)=0,175(м2) . б) A1A2=D1D2, A1A2 D1D2(по св-ву призмы) A1A2D2D1-параллелограмм(по признаку),
но D1D2 (A2B2C2) (по св-ву), значит, D1D2 A2D2(по определению) A1A2D2D1 -прямоугольник(по определению), т.е. SA1A2D2D1=A1A2 A2D2, т.е.
Sсечения2=70 2 32=4480(см2)=0,448(м2)
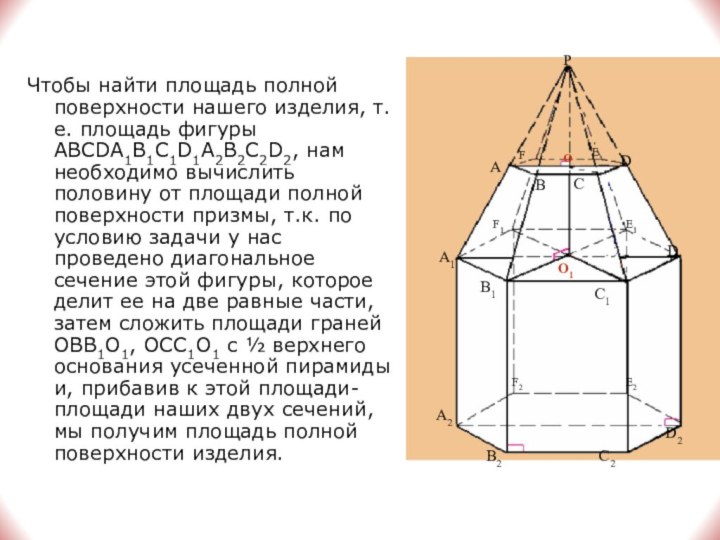
Слайд 18 Чтобы найти площадь полной поверхности нашего изделия, т.е.
площадь фигуры ABCDA1B1C1D1A2B2C2D2, нам необходимо вычислить половину от площади
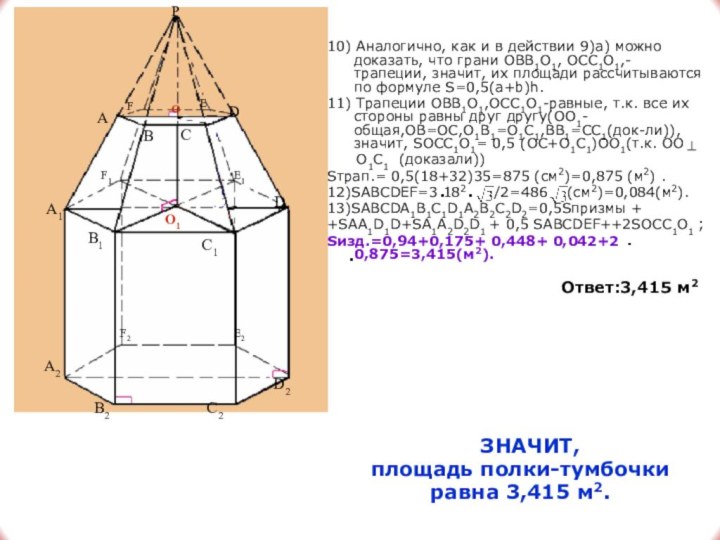
полной поверхности призмы, т.к. по условию задачи у нас проведено диагональное сечение этой фигуры, которое делит ее на две равные части, затем сложить площади граней OBB1O1, OCC1O1 с ½ верхнего основания усеченной пирамиды и, прибавив к этой площади-площади наших двух сечений, мы получим площадь полной поверхности изделия.Слайд 19 10) Аналогично, как и в действии 9)а) можно
доказать, что грани OBB1O1, OCC1O1,- трапеции, значит, их площади
рассчитываются по формуле S=0,5(a+b)h.11) Трапеции OBB1O1,OCC1O1-равные, т.к. все их стороны равны друг другу(OO1-общая,OB=OC,O1B1=O1C1,BB1=CC1(док-ли)), значит, SOCC1O1= 0,5 (OC+O1С1)OO1(т.к. OO1
O1C1 (доказали))
Sтрап.= 0,5(18+32)35=875 (см2)=0,875 (м2) .
12)SABCDEF=3 182 /2=486 (см2)=0,084(м2).
13)SABCDA1B1C1D1A2B2C2D2=0,5Sпризмы +
+SAA1D1D+SA1A2D2D1 + 0,5 SABCDEF++2SOCC1O1 ;
Sизд.=0,94+0,175+ 0,448+ 0,042+2 0,875=3,415(м2).
Ответ:3,415 м2
ЗНАЧИТ,
площадь полки-тумбочки
равна 3,415 м2.