Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему по геометрии на тему Параллельность прямых и плоскостей (10 класс)

Содержание

????АМN и DCAB1 и МN MN и ВСAB1 и DC1Как располагаются прямыеII∸∩∸RNM
Параллельность прямой и плоскости по учебнику И.М. Смирновой (может применяться и ????АМN и DCAB1 и МN MN и ВСAB1 и DC1Как располагаются прямыеII∸∩∸RNM Как могут располагаться прямая и плоскость?Лежать в плоскостиНе иметь с плоскостью ни Определение параллельности прямой и плоскостиПрямая и плоскость называются параллельными, если они не Прямая и плоскостьИмеют общие точкиНе имеют общих точекИмеют одну общую точку (пересекаются)Имеют Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту abТЕОРЕМА (ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМОЙ И ПЛОСКОСТИ)Если прямая не лежащая в данной плоскости, Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая Две прямые, параллельные третьей прямой, параллельны между собой.Теорема.(Признак параллельности прямых): св-во транзитивностиaс Задача. Доказать, что ребра одного основания призмы параллельны другому основанию этой призмы.Решение. Задача.Через точку, не принадлежащую данной плоскости, провести прямую, параллельную этой плоскости. Сколько АBCDMNKL. Задача. Докажите, что середины Задача. Даны две скрещивающиеся прямые. Как через одну из них провести плоскость, параллельную другой? Спасибо за совместную работу Пространственным четырёхугольником называется четырехугольник, вершины которого не лежат в одной плоскости.АDBCназад
Слайды презентации

Слайд 2 ?
?
?
?
А
МN и DC
AB1 и МN
MN

????АМN и DCAB1 и МN MN и ВСAB1 и DC1Как располагаются прямыеII∸∩∸RNM

и ВС
AB1 и DC1
Как располагаются прямые
II
∸
∩
∸
R
N
M

Слайд 3 Как могут располагаться прямая и плоскость?
Лежать в плоскости
Не

Как могут располагаться прямая и плоскость?Лежать в плоскостиНе иметь с плоскостью

иметь с плоскостью ни одной общей точки
Пересекать
плоскость

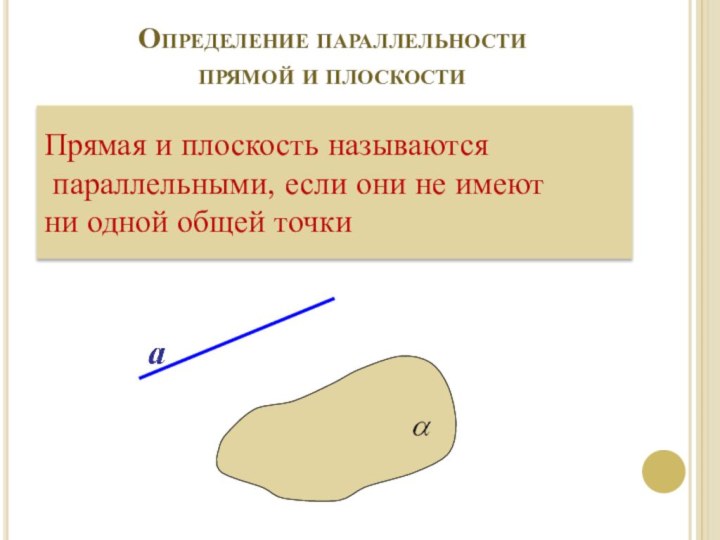
Слайд 4 Определение параллельности прямой и плоскости
Прямая и плоскость называются

Определение параллельности прямой и плоскостиПрямая и плоскость называются параллельными, если они

параллельными, если они не имеют
ни одной общей точки

Слайд 5 Прямая и плоскость
Имеют общие точки
Не имеют общих точек
Имеют

Прямая и плоскостьИмеют общие точкиНе имеют общих точекИмеют одну общую точку

одну общую точку (пересекаются)
Имеют более одной общей точки

(прямая лежит в плоскости)

ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ

(параллельны)

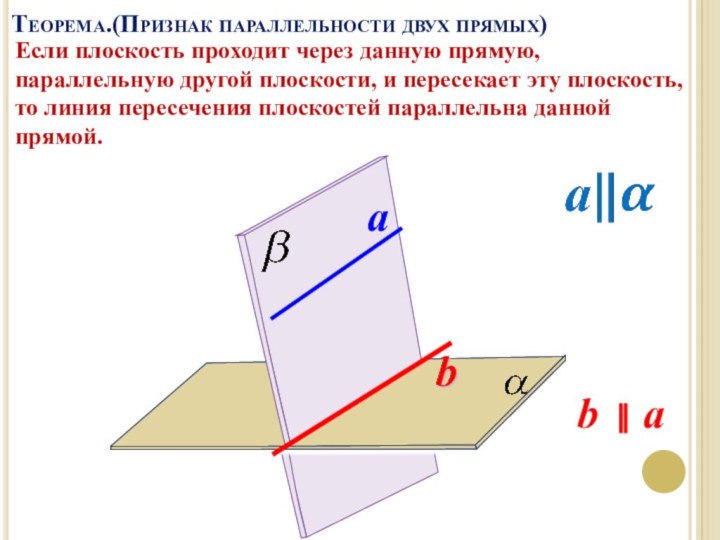
Слайд 6 Если плоскость проходит через данную прямую, параллельную другой

Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает

плоскости, и пересекает эту плоскость, то линия пересечения плоскостей

параллельна данной прямой.

a

b ⃦ a

Теорема.(Признак параллельности двух прямых)

Слайд 7 a
b
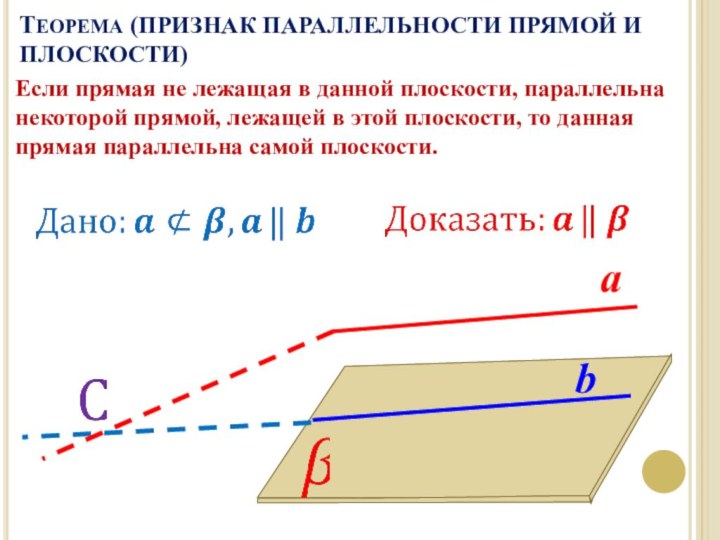
ТЕОРЕМА (ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМОЙ И ПЛОСКОСТИ)
Если прямая не

abТЕОРЕМА (ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМОЙ И ПЛОСКОСТИ)Если прямая не лежащая в данной

лежащая в данной плоскости, параллельна некоторой прямой, лежащей в

этой плоскости, то данная прямая параллельна самой плоскости.

Слайд 8 Если одна из двух параллельных прямых параллельна данной

Если одна из двух параллельных прямых параллельна данной плоскости, то другая

плоскости, то другая прямая либо также параллельна данной плоскости,

либо лежит в этой плоскости.

Слайд 9 Две прямые, параллельные третьей прямой, параллельны между собой.
Теорема.(Признак

Две прямые, параллельные третьей прямой, параллельны между собой.Теорема.(Признак параллельности прямых): св-во транзитивностиaс

параллельности прямых): св-во транзитивности
a
с

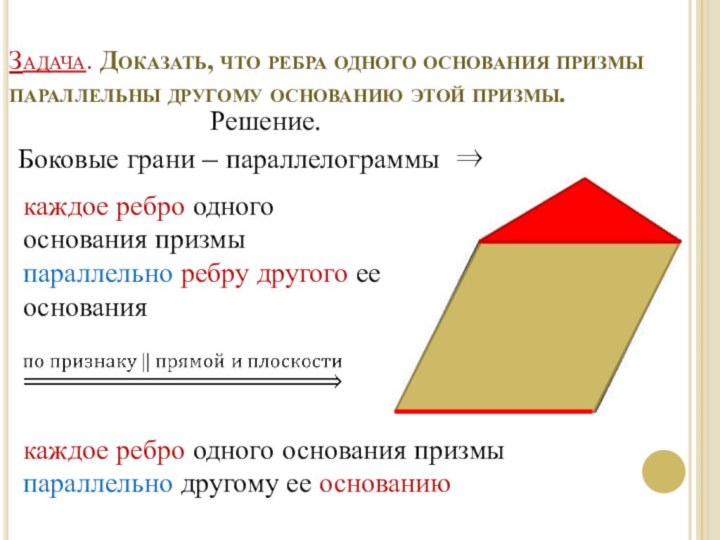
Слайд 10 Задача. Доказать, что ребра одного основания призмы параллельны

Задача. Доказать, что ребра одного основания призмы параллельны другому основанию этой

другому основанию этой призмы.
Решение.
Боковые грани – параллелограммы ⇒


каждое ребро одного основания призмы параллельно ребру другого ее основания

каждое ребро одного основания призмы параллельно другому ее основанию

Слайд 11 Задача.Через точку, не принадлежащую данной плоскости, провести прямую,

Задача.Через точку, не принадлежащую данной плоскости, провести прямую, параллельную этой плоскости.

параллельную этой плоскости. Сколько можно построить таких прямых?
Решение.
Итак, b

– искомая прямая.

Таких прямых можно построить бесконечно много.

Слайд 12

Слайд 13

Слайд 14 А
B
C
D
M
N
K
L
. Задача. Докажите, что середины сторон пространственного четырёхугольника

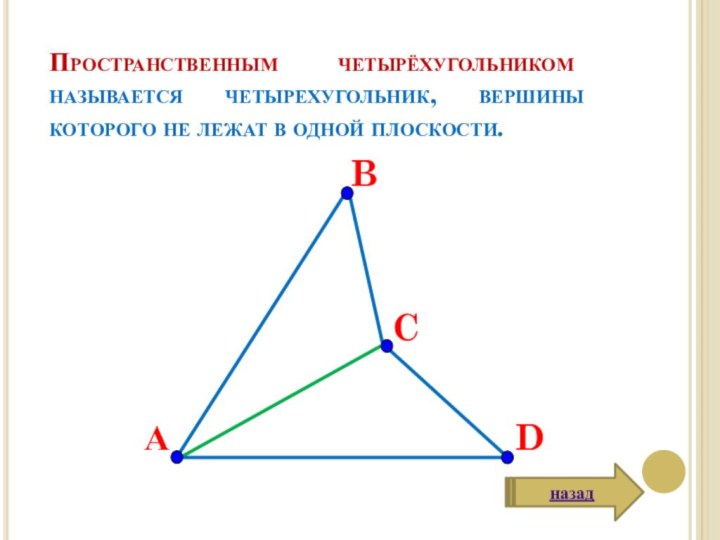
АBCDMNKL. Задача. Докажите, что середины сторон пространственного четырёхугольника

являются вершинами параллелограмма.
Доказательство.
ABCD-пространственный четырехугольник,
М, N, K, L

– середины сторон
АС – диагональ ABCD.

MN – средняя линия △АВС,
LK – средняя линия △АСD.

MN ⃦ AC и LK ⃦ AC

MNKL – параллелограмм.

Что и т.д.

вспомним

Слайд 15 Задача. Даны две скрещивающиеся прямые. Как через одну

Задача. Даны две скрещивающиеся прямые. Как через одну из них провести плоскость, параллельную другой?

из них провести плоскость, параллельную другой?

Слайд 16 Спасибо за совместную работу

Спасибо за совместную работу
  • Имя файла: prezentatsiya-po-geometrii-na-temu-parallelnost-pryamyh-i-ploskostey-10-klass.pptx
  • Количество просмотров: 153
  • Количество скачиваний: 0
- Предыдущая Презентация интеллектуальной интерактивной игры Для тех, кто любит математику
Следующая - Оперативное хранение документов. Номенклатура дел. Формирование дел.

Похожие презентации

Площадь круга Площадь круга 156
Презентация к уроку Параллельные прямые Презентация к уроку Параллельные прямые 129
Презентация по математике Лист Мёбиуса Презентация по математике Лист Мёбиуса 165
Некоторые свойства прямоугольного треугольника урок изучения нового материала 7 класс Некоторые свойства прямоугольного треугольника урок изучения нового материала 7 класс 169
Презентация по геометрии на тему Теория по планиметрии (проектная работа) Презентация по геометрии на тему Теория по планиметрии (проектная работа) 181
Гармония в золотом сечении Гармония в золотом сечении 187
Преобразования фигур. Движение Преобразования фигур. Движение 171
Свойства равнобедренного треугольника Свойства равнобедренного треугольника 163
Свойства трапеции Свойства трапеции 169
Презентация по математике на тему Школа Пифагора(8класс) Презентация по математике на тему Школа Пифагора(8класс) 170
Три кита геометрии Три кита геометрии 324
Презентация. Гл. 1. Урок 6. Трапеция. Презентация. Гл. 1. Урок 6. Трапеция. 165
Презентация по геометрии на тему Признаки параллелограмма (8 класс) Презентация по геометрии на тему Признаки параллелограмма (8 класс) 183
Симметрия в пространстве Симметрия в пространстве 162
Презентация по геометрии на тему Формулы для радиусов вписанных и описанных окружностей правильных многоугольников. Презентация по геометрии на тему Формулы для радиусов вписанных и описанных окружностей правильных многоугольников. 217
Квадрат теңдеуге келтірілетін теңдеулер Квадрат теңдеуге келтірілетін теңдеулер 148
Четырёхугольники, их признаки и свойства Четырёхугольники, их признаки и свойства 131
Подобие треугольников 8 класс Подобие треугольников 8 класс 169
Скрещивающиеся прямые Скрещивающиеся прямые 163
Соотношения между сторонами и углами треугольника Соотношения между сторонами и углами треугольника 155
Презентация по математике на тему Построение фигур одним росчерком пера. Презентация по математике на тему Построение фигур одним росчерком пера. 250
Прямоугольник и квадрат Прямоугольник и квадрат 149
Параллельные прямые Параллельные прямые 154
Симметрия в геометрии Симметрия в геометрии 166
Презентация Задачи на построение Презентация Задачи на построение 161
Аксиомы стереометрии Аксиомы стереометрии 140
Векторы в пространстве Векторы в пространстве 184
Нахождение площади параллелограмма Нахождение площади параллелограмма 207
Уравнение эллипса Уравнение эллипса 158
Цилиндром называется тело Цилиндром называется тело 165