данной фигуры сместить каким-нибудь образом, то мы получим новую
фигуру. Говорят, что эта фигура получена преобразованием из данной.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть



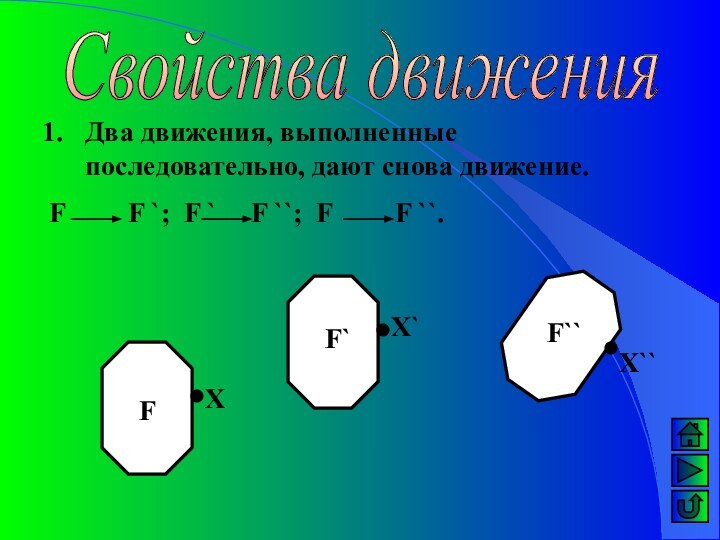










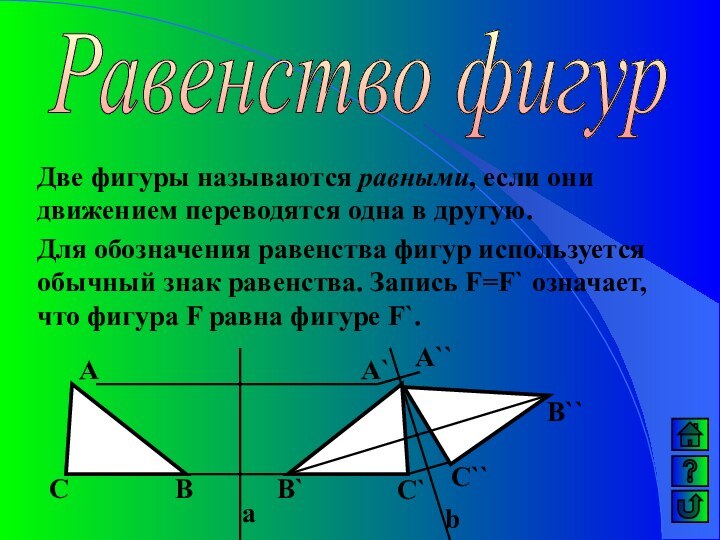
F
F`
F``
Х
Х`
Х``
Следовательно:
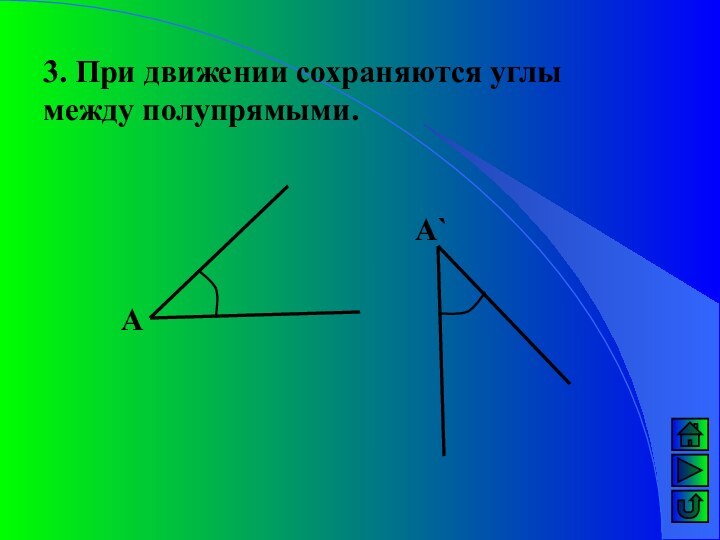
При движении прямые переходят в прямые: а а`.
А
А`
B
B`
X
X`
O
O`
Y
Y`
a`
а
полупрямые – в полупрямые:OY O`Y`.
отрезки – в отрезки: АВ А`B`; Х Х`.
Точка X` называется симметричной точке Х относительно точки О. Точка, симметричная точке О, есть сама точка О. Очевидно, что точка, симметричная точке Х`, есть точка Х.
Х
Х`
О
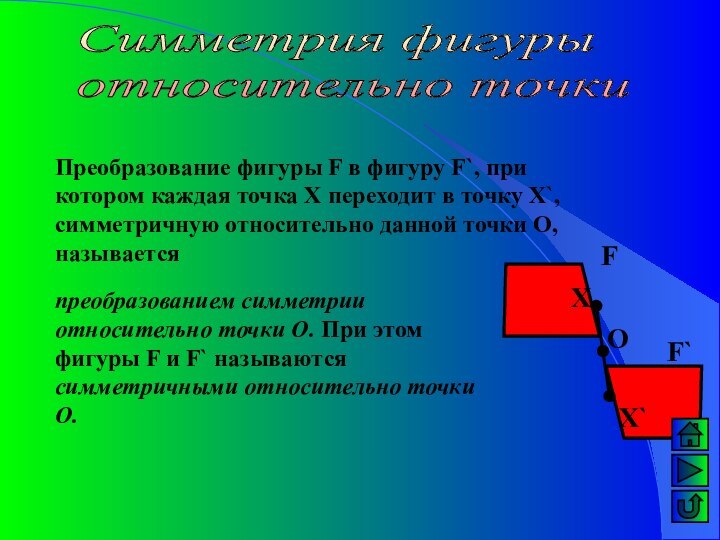
F
F`
X
X`
О
преобразованием симметрии относительно точки О. При этом фигуры F и F` называются симметричными относительно точки О.
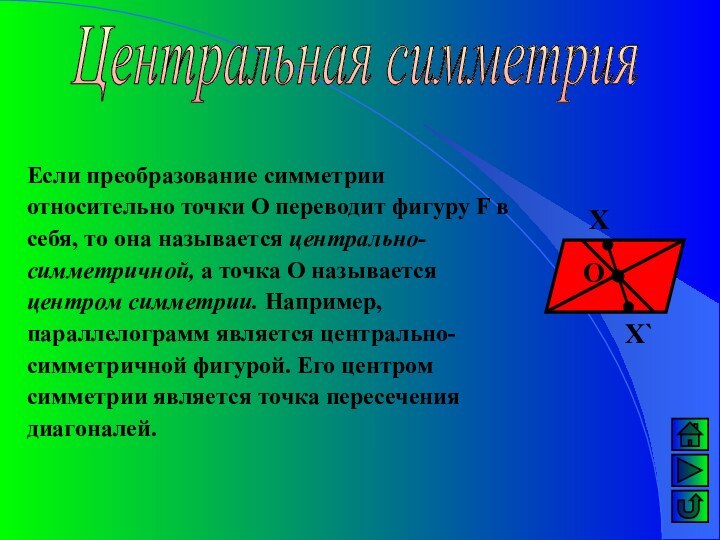
Х
Х`
О
и опустим перпендикуляр АХ на прямую g.
На продолжении перпендикуляра за точку А отложим отрезок АХ`, равные отрезку АХ.
Точка Х `называется симметричной точке Х относительно прямой g.
Если точка Х лежит на прямой g, то симметричная ей точка есть сама точка Х.
Х
Х`
g
A
g
X
X`
F
F`
О
Х
Х`
Х
Х`
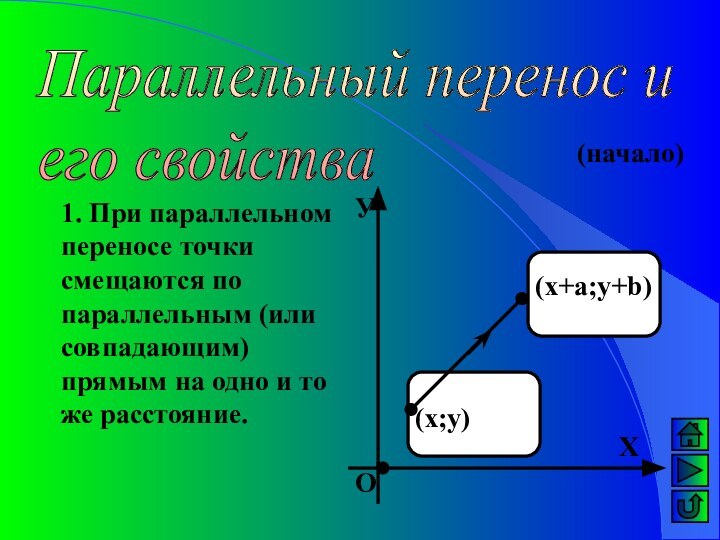
(х;у)
(х+а;у+b)
У
Х
О
(начало)
Х
Х`
А
А`
О