- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему ПРИЗМА.Сечения призмы
Содержание
- 2. Виды призм.Прямая.Правильная.Наклонная.
- 3. Все призмы делятся на прямые и наклонные.
- 4. Свойства призмы. 1. Основания призмы являются
- 5. Сечение призмы 1. Сечение призмы плоскостью, параллельной
- 6. Наиболее доступными и эффективными методами построения сечения
- 7. Сечение правильной призмы. 1. Сечение правильной призмы
- 8. Задача.Дано: Сторона основания правильной треугольной призмы равна
- 9. Дано: правильная призма, АВ=3см,
- 10. Применение призмы в архитектуре
- 11. Скачать презентацию
- 12. Похожие презентации
Виды призм.Прямая.Правильная.Наклонная.

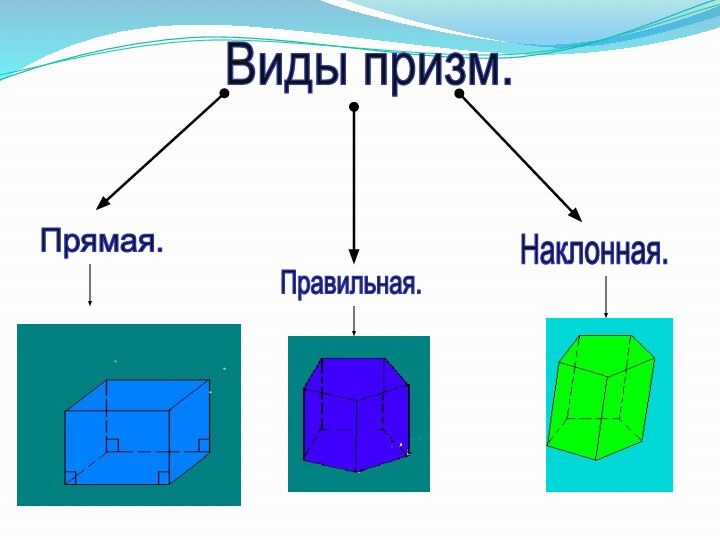
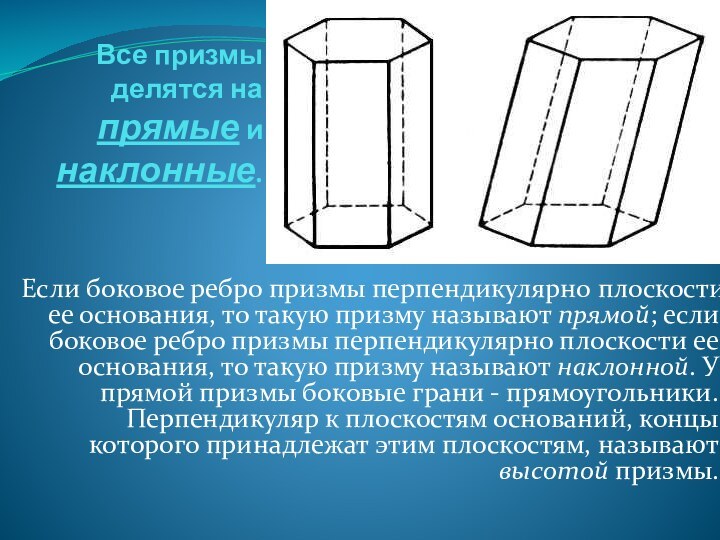





Слайд 4
Свойства призмы.
1. Основания призмы являются равными многоугольниками.
2. Боковые
грани призмы являются параллелограммами.
3о. Боковые ребра призмы равны.
Слайд 5
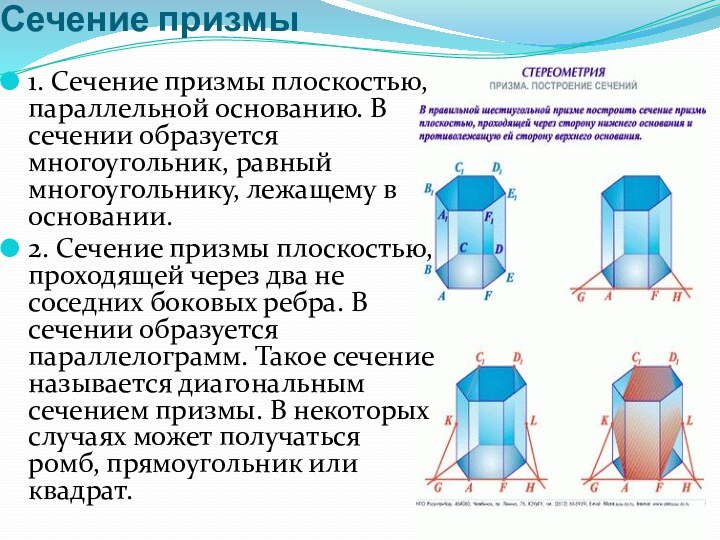
Сечение призмы
1. Сечение призмы плоскостью, параллельной основанию. В
сечении образуется многоугольник, равный многоугольнику, лежащему в основании.
2. Сечение призмы
плоскостью, проходящей через два не соседних боковых ребра. В сечении образуется параллелограмм. Такое сечение называется диагональным сечением призмы. В некоторых случаях может получаться ромб, прямоугольник или квадрат.Слайд 6 Наиболее доступными и эффективными методами построения сечения призмы
являются три метода:
1. Метод следов.
3. Комбинированный метод.
2. Метод вспомогательных
сечений.www.matematika-na5.narod.ru
Слайд 7
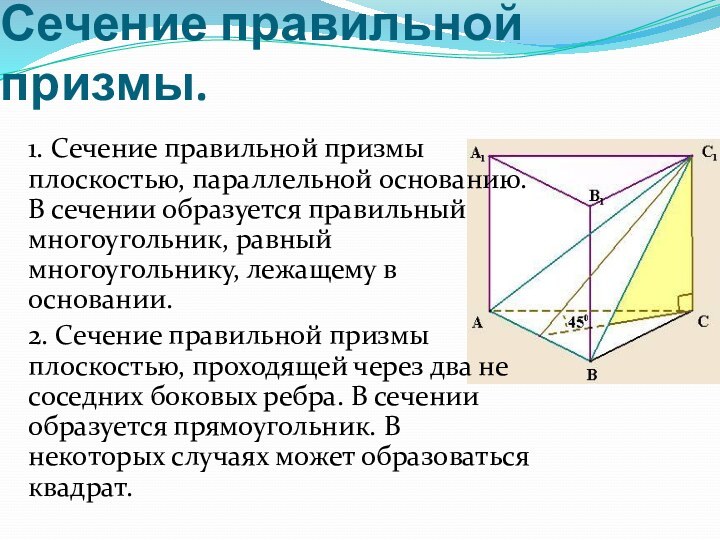
Сечение правильной призмы.
1. Сечение правильной призмы плоскостью,
параллельной основанию. В сечении образуется правильный многоугольник, равный многоугольнику,
лежащему в основании.2. Сечение правильной призмы плоскостью, проходящей через два не соседних боковых ребра. В сечении образуется прямоугольник. В некоторых случаях может образоваться квадрат.
Слайд 8
Задача.
Дано: Сторона основания правильной треугольной призмы равна 8
см, боковое ребро - 6 см. Найдите Sсеч, проходящего
через сторону верхнего основания и противолежащую вершину нижнего основания.Решение: Треугольник A1B1C1 - равнобедренный(A1B=C1B как диагональ равных граней)
1)Рассмотрим треугольник BCC1– прямоугольный
BC12=BС2+CC12
BC1= √ 64+36=10 см
2) Рассмотрим треугольник BMC1– прямоугольный
BC12=BM2+MC12
BM2=BC12-MC12
BM2=100-16=84
BM= √ 84=2 √ 21 см
3) Sсеч=12 A1C1*BM= 12*2√ 21 см*8=8 √ 21
Слайд 9
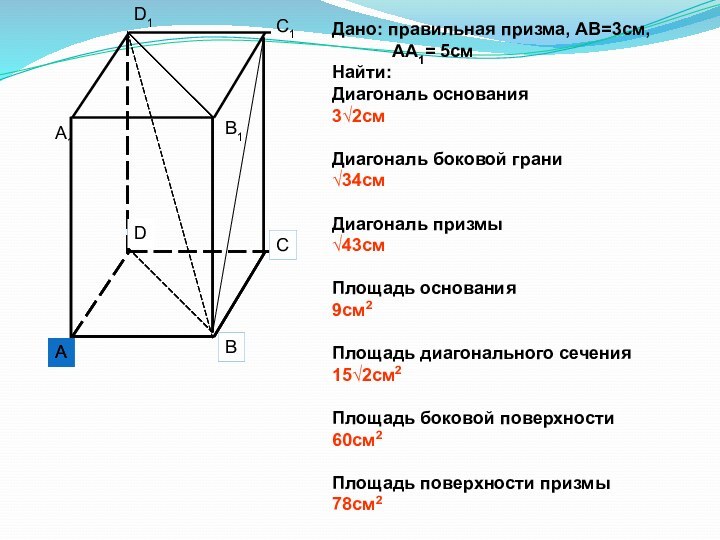
Дано: правильная призма, АВ=3см,
АА1= 5см
Найти:
Диагональ основания
3√2см
Диагональ боковой грани
√34см
Диагональ призмы
√43см
Площадь основания
9см2
Площадь
диагонального сечения15√2см2
Площадь боковой поверхности
60см2
Площадь поверхности призмы
78см2