- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему : Круги Эйлера.
Содержание
- 2. Цель исследования: Знакомство с новым методом решения
- 3. Актуальность работы состоит в том, что задачи
- 4. - Познакомиться с биографией одного из величайших
- 5. БиографияЛеонард Эйлер родился 15 апреля 1707 года
- 6. Великий учёный - Леонард Эйлер занимает одно
- 7. Эйлер активно трудился до последних дней. 7
- 8. – геометрическая схема, с помощью которой можно
- 9. В математике множеством называют совокупность, набор каких-либо
- 10. Покажем, например, С помощью диаграммы Эйлера, что
- 11. Пересечением двух множеств А и В называют
- 12. Объединением С двух множеств А и В
- 13. Разность множествРазностью А\В множеств А и В
- 14. В детском саду 52 ребенка. Каждый из
- 15. Все мои подруги выращивают в своих квартирах
- 16. Гарри Поттер, Рон и ГермионаНа полке стояло
- 17. В классе 30 человек. 20 из них
- 18. Из 100 отдыхающих на турбазе «Графское»,30 детей
- 19. ВыводыПрименение кругов Эйлера позволяет легко решить задачи,
- 20. "Чем нагляднее метод, тем очевиднее решение"
- 21. Скачать презентацию
- 22. Похожие презентации




















Слайд 3 Актуальность работы состоит в том, что задачи имеют
практический характер. Задачи развивают логическое мышление, заставляют задумываться, подходить
к решению какой либо проблемы с разных сторон, выбирать из множества способов решения наиболее простой, легкий путь.Актуальность
Слайд 4 - Познакомиться с биографией одного из величайших ученых-математиков
Леонарда Эйлера;
- Изучить теоретические основы понятия «Круги Эйлера»;
- Решить
ряд задач вышеназванным методом;Задачи исследования:
Слайд 5
Биография
Леонард Эйлер родился 15 апреля 1707 года в
семье пастора, жившей в швейцарском городке Базеле.
Начальное обучение Эйлер
получил под руководством отца, который готовил его к духовной карьере. С детства увлекался математикой. В 13 лет Леонард Эйлер стал студентом факультета искусств Базельского университета.
В 17 лет был удостоен учёной степени магистра.
В 19-лет Эйлер был включен в число кандидатов на должность профессора физики.
Слайд 6 Великий учёный - Леонард Эйлер занимает одно из
первых мест в истории мировой науки. Полное собрание его
трудов составляет 72 тома, более 850 научных работ. Этот тихий и скромный человек, полностью ослепший, много работал, совершив великое множество научных открытий. С точки зрения математики, XVIII век — это век Эйлера.Эйлер впервые увязал анализ, алгебру, тригонометрию, теорию чисел и др. дисциплины в единую систему, и добавил немало собственных открытий. Значительная часть математики преподаётся с тех пор «по Эйлеру».
Слайд 7 Эйлер активно трудился до последних дней. 7 сентября
после обеда, проведённого в кругу семьи, беседуя с астрономом
А. И. Лекселем о недавно открытой планете Уран и её орбите, он внезапно почувствовал себя плохо и потерял сознание. Через несколько часов, так и не приходя в сознание, он скончался от кровоизлияния в мозг.Похоронен на Смоленском лютеранском кладбище в Петербурге.
Умирая, он оставил много рукописей, которые Петербургская академия публиковала в течение последующих 47 лет.
Слайд 8 – геометрическая схема, с помощью которой можно изобразить
отношения между множествами.
Впервые он использовал их
в письмах к немецкой принцессе. Эйлер писал тогда, что круги очень подходят для того, чтобы «облегчить наши размышления.» Наряду с кругами в подобных задачах применяют прямоугольники и другие фигуры.
Круги Эйлера
Слайд 9 В математике множеством называют совокупность, набор каких-либо предметов
(объектов).
Предметы, составляющие множество, называются его элементами.
Множества обычно обозначаются большими
буквами латинского алфавита: А, В, С,… .Термин «множество» употребляется независимо от того, много или мало в этом множестве элементов, Множество, не содержащее ни одного элемента, называется пустым и обозначается символом Ø
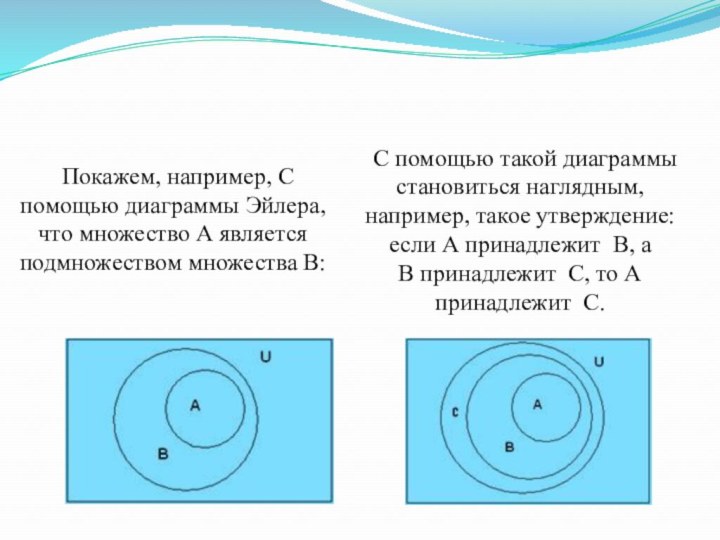
Слайд 10 Покажем, например, С помощью диаграммы Эйлера, что множество
А является подмножеством множества В:
С помощью такой диаграммы
становиться наглядным, например, такое утверждение: если А принадлежит В, а В принадлежит С, то А принадлежит С.Слайд 11 Пересечением двух множеств А и В называют множество,
состоящее из всех общих элементов множеств А и В,
т. е. Из всех элементов, которые принадлежат и множеству А, и множеству В.А ∩ В
Слайд 12 Объединением С двух множеств А и В называется
множество, состоящее из всех элементов, принадлежащих множеству А или
множеству В.Обозначают это так: С = А U В.
Иными словами, в объединение входят все элементы, принадлежащие хотя бы одному из множеств.
А U В
Слайд 13
Разность множеств
Разностью А\В множеств А и В называется
множество, состоящее из всех элементов множества А, которые не
принадлежат множеству В.Слайд 14 В детском саду 52 ребенка. Каждый из них
любит пирожное или мороженое. Половина детей любит пирожное, а
20 человек - пирожное и мороженое. Сколько детей любит мороженое?Решение:
Так как 26 половина детей любит пирожные, а 20 - и пирожные, и мороженое, то исключительно пирожное любят ровно 6 человек. Всего ребят 52, из них 6 - любители только пирожных, значит, 52 – 6 = 46 человек, которые любят мороженое.
Слайд 15 Все мои подруги выращивают в своих квартирах какие-нибудь
растения. Шестеро из них разводят кактусы, а пятеро —
фиалки. И только у двоих есть и кактусы и фиалки. Угадайте, сколько у меня подруг?Решение: : Изобразим два круга, так как у нас два вида цветовПоскольку у некоторых подруг есть и те, и другие цветы, то круги нарисуем так, чтобы у них была общая часть. В этой общей части ставим цифру 2 так как кактусы и фиалки у двоих. В оставшейся части «кактусового» круга ставим цифру 4 (6 − 2 = 4). В свободной части «фиалкового» круга ставим цифру 3 (5 − 2 = 3). А теперь рисунок сам подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг.
Слайд 16
Гарри Поттер, Рон и Гермиона
На полке стояло 26
волшебных книг по заклинаниям. Из них 4 прочитал и
Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал Рон?Решение
Учитывая условия задачи, чертеж будет таков:
Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона,
то 11 – 4 – 2 = 5 – книг прочитал только Гарри. Следовательно,
26 – 7 – 2 – 5 – 4 = 8 – книг прочитал Рон.
Ответ. 8 книг прочитал Рон.
5
8
Слайд 17 В классе 30 человек. 20 из них каждый
день пользуются метро, 15 — автобусом, 23 — троллейбусом,
10 — и метро, и троллейбусом, 12 — и метро, и автобусом, 9 — и троллейбусом, и автобусом.Сколько человек ежедневно пользуются всеми тремя видами транспорта?
Пусть х человек пользуется всеми тремя видами транспорта. Тогда пользуются только метро и троллейбусом — (10 − х) человек, только автобусом и троллейбусом — (9 − х) человек, только метро и автобусом — (12 − х) человек. Найдем, сколько человек пользуется одним только метро:
20 − (12 − х) − (10 − х) − х = х − 2
Аналогично получаем: х − 6 — только автобусом и х + 4 — только троллейбусом, так как всего 30 человек, составляем уравнение:
Х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30. отсюда х = 3
Слайд 18
Из 100 отдыхающих на турбазе «Графское»,
30 детей -
отличники учебы,
28 - участники олимпиад,
42 - спортсмены.
8 учащихся одновременно
участники олимпиад и спортсмены,10 – участники олимпиад и отличники,
5 – спортсмены и отличники учебы,
3 – и отличники, и участники олимпиад, и спортсмены.
Сколько отдыхающих не относятся ни к одной из групп?
Решение:
20+13+30+3+5+7+2=80 (детей)
100-80=20 (детей не входят ни в одну из групп)