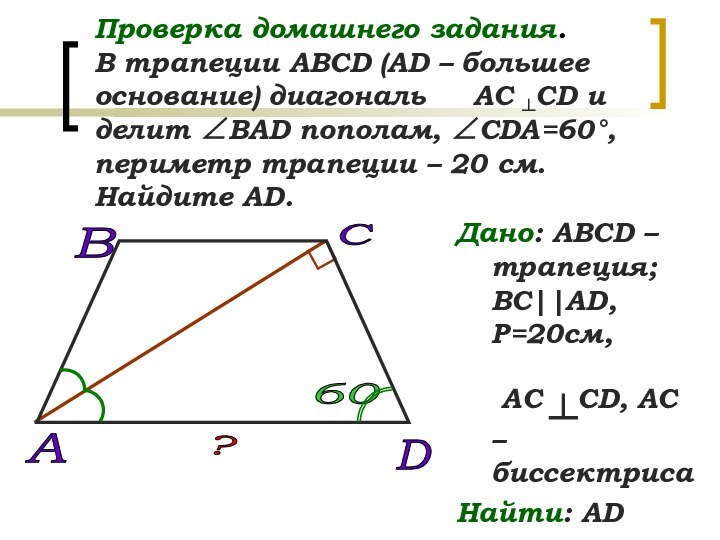
(АD – большее основание) диагональ АС ┴СD
и делит ∠ВАD пополам, ∠СDА=60°, периметр трапеции – 20 см. Найдите АD.Дано: АВСD –трапеция; BC||AD, Р=20см,
АС ┴СD, АС – биссектриса
Найти: AD
?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть



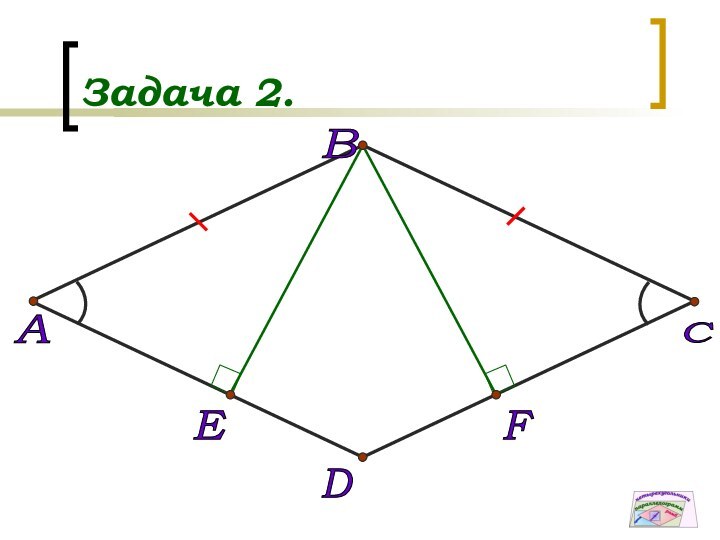
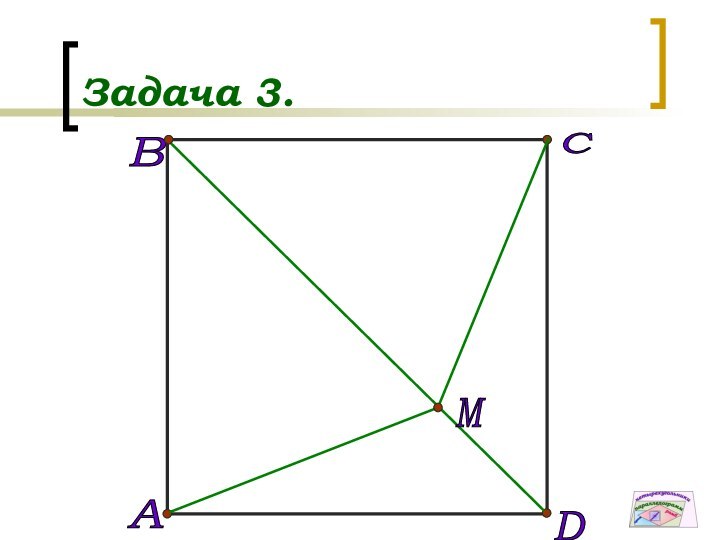


Дано: АВСD –трапеция; BC||AD, Р=20см,
АС ┴СD, АС – биссектриса
Найти: AD
?