- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
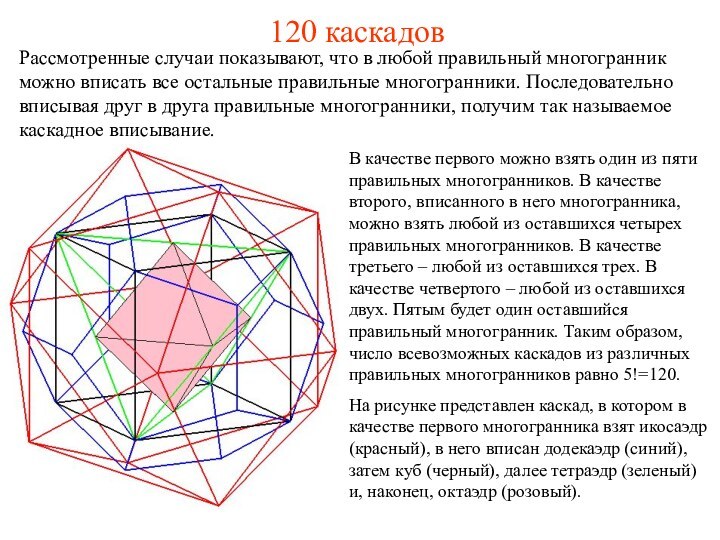
Презентация на тему Каскады многогранников
Содержание
- 2. Куб и тетраэдрТетраэдр можно вписать в куб так, что вершинами тетраэдра будут некоторые вершины куба.
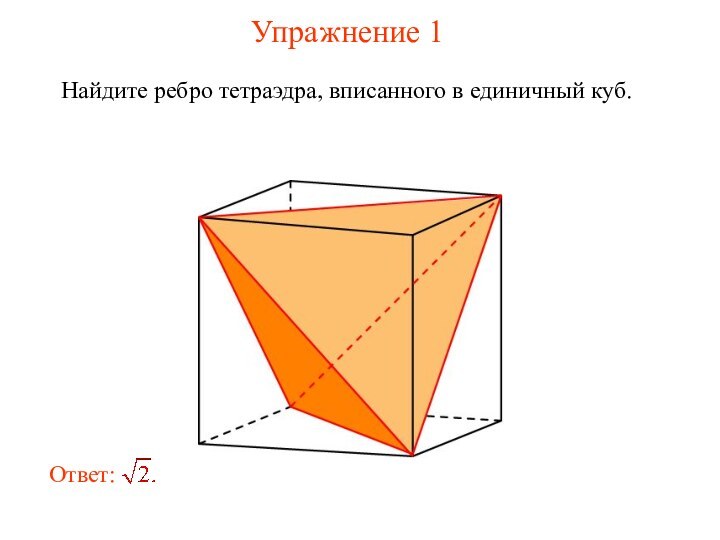
- 3. Упражнение 1Найдите ребро тетраэдра, вписанного в единичный куб.
- 4. Куб и октаэдрВ куб можно вписать октаэдр.
- 5. Упражнение 2Найдите ребро октаэдра, вписанного в единичный куб.
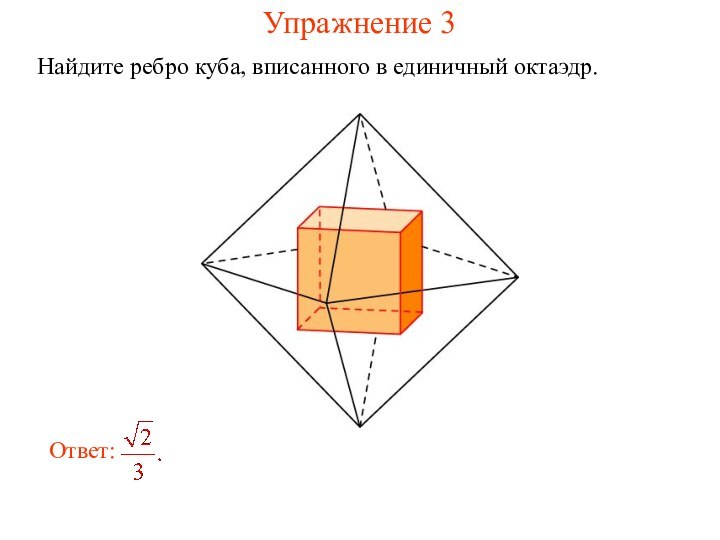
- 6. Упражнение 3Найдите ребро куба, вписанного в единичный октаэдр.
- 7. Куб и икосаэдр
- 8. Упражнение 4Впишем в куб икосаэдр. Для этого
- 9. Куб и додекаэдр
- 10. Упражнение 5Впишем в куб додекаэдр. Для этого
- 11. Додекаэдр и икосаэдрВ додекаэдр можно вписать икосаэдр.
- 12. Упражнение 6Найдите ребро додекаэдра, вписанного в единичный икосаэдр.
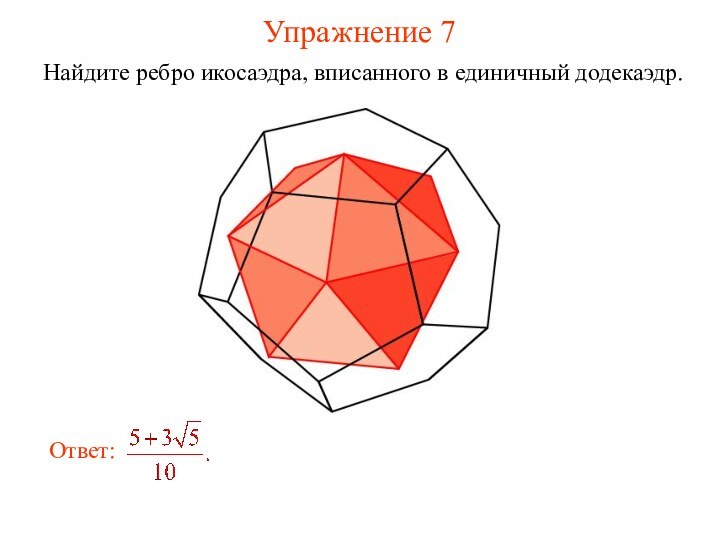
- 13. Упражнение 7Найдите ребро икосаэдра, вписанного в единичный додекаэдр.
- 14. Додекаэдр и кубКуб можно вписать в додекаэдр так, что вершинами куба будут некоторые вершины додекаэдра.
- 15. Упражнение 8Найдите ребро куба, вписанного в единичный додекаэдр.
- 16. Додекаэдр и тетраэдрВ додекаэдр можно вписать куб
- 17. Упражнение 9Найдите ребро тетраэдра, вписанного в единичный додекаэдр.
- 18. Додекаэдр и октаэдр
- 19. Упражнение 10 Найдите ребро октаэдра, вписанного в единичный додекаэдр.
- 20. Икосаэдр и кубВ икосаэдр можно вписать додекаэдр,
- 21. Упражнение 11Найдите ребро куба, вписанного в единичный икосаэдр.
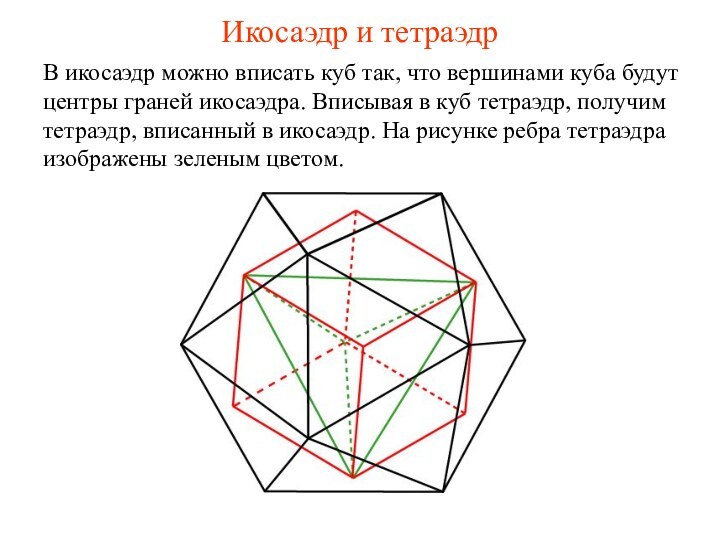
- 22. Икосаэдр и тетраэдрВ икосаэдр можно вписать куб
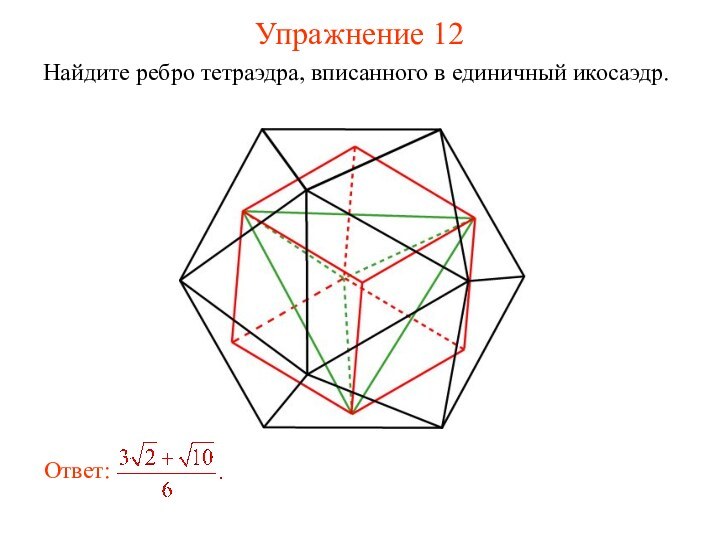
- 23. Упражнение 12Найдите ребро тетраэдра, вписанного в единичный икосаэдр.
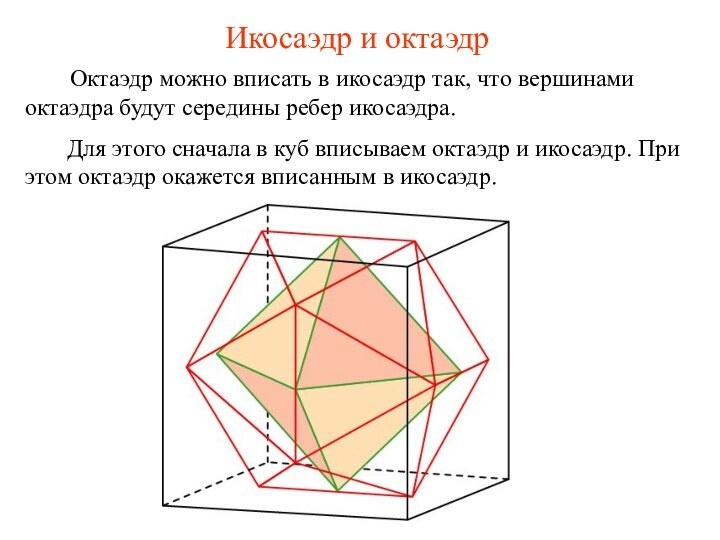
- 24. Икосаэдр и октаэдр
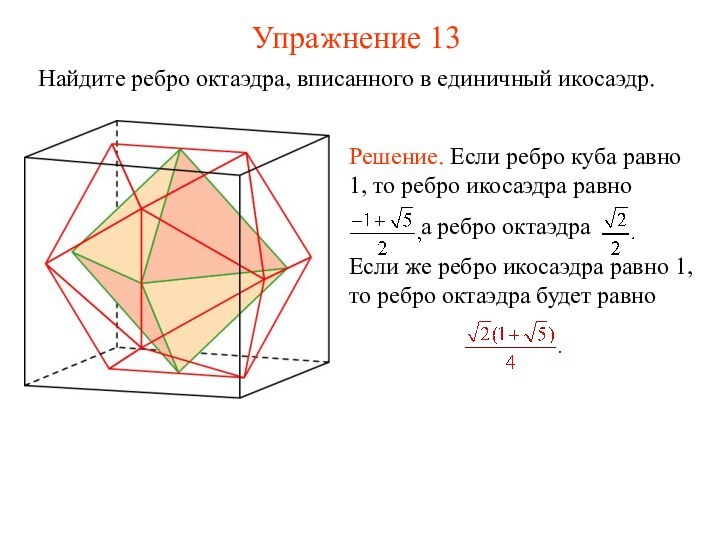
- 25. Упражнение 13 Найдите ребро октаэдра, вписанного в единичный икосаэдр.
- 26. Октаэдр и тетраэдрВ октаэдр можно вписать куб
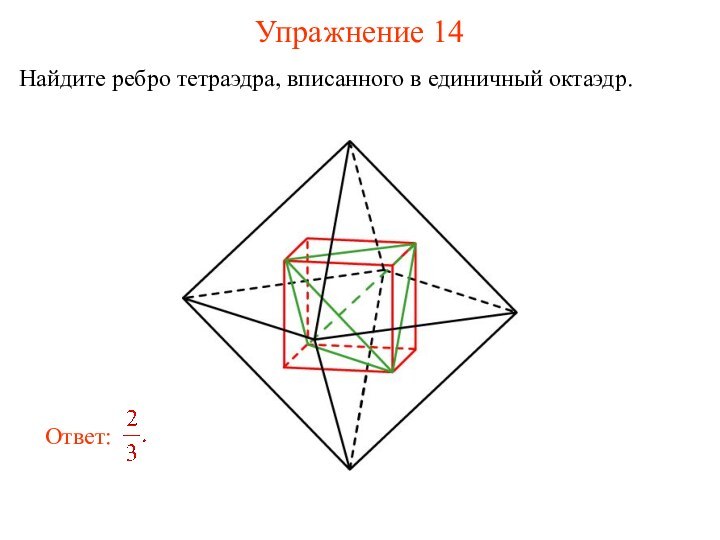
- 27. Упражнение 14Найдите ребро тетраэдра, вписанного в единичный октаэдр.
- 28. Октаэдр и икосаэдр
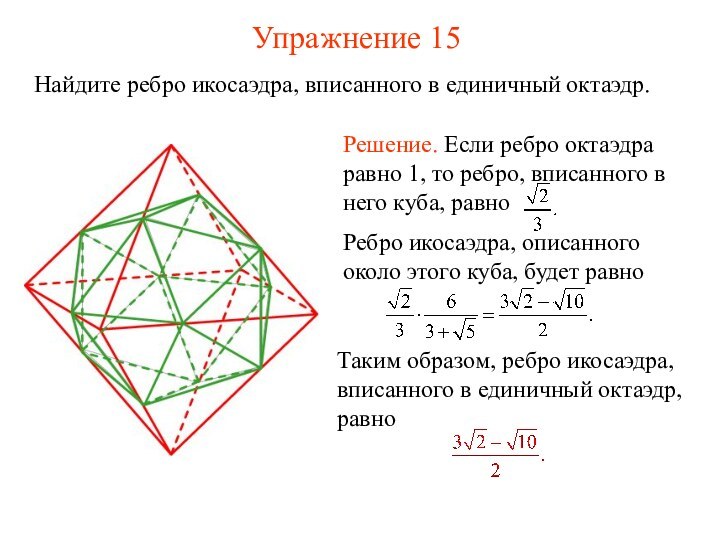
- 29. Упражнение 15 Найдите ребро икосаэдра, вписанного в единичный октаэдр.
- 30. Октаэдр и додекаэдр
- 31. Упражнение 16 Найдите ребро додекаэдра, вписанного в единичный октаэдр.
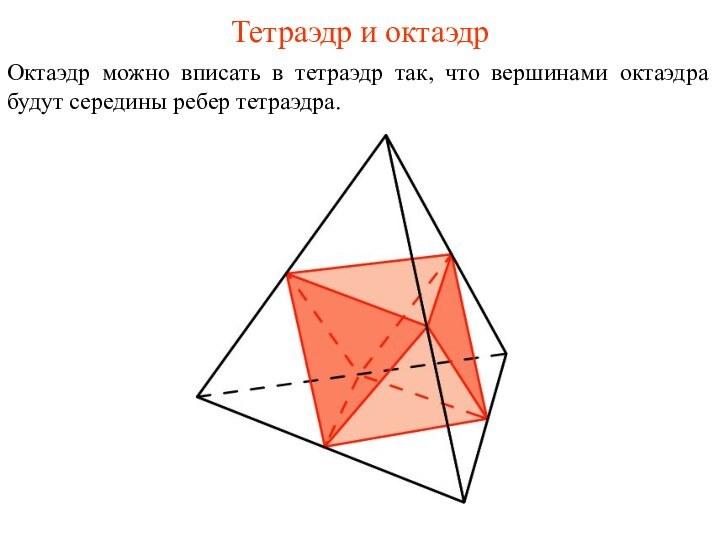
- 32. Тетраэдр и октаэдрОктаэдр можно вписать в тетраэдр так, что вершинами октаэдра будут середины ребер тетраэдра.
- 33. Упражнение 17Найдите ребро октаэдра, вписанного в единичный тетраэдр.
- 34. Тетраэдр и кубВпишем в тетраэдр октаэдр, а
- 35. Упражнение 18Найдите ребро куба, вписанного в единичный тетраэдр.
- 36. Тетраэдр и икосаэдр Икосаэдр можно вписать в
- 37. Упражнение 19 Найдите ребро икосаэдра, вписанного в единичный тетраэдр.
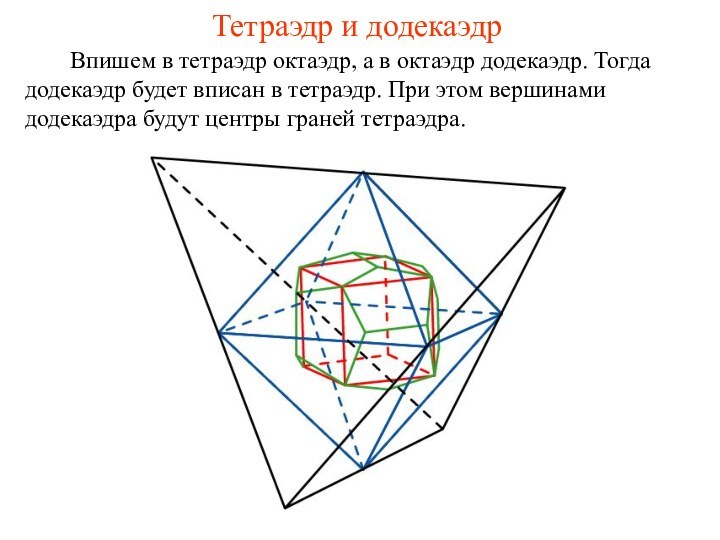
- 38. Тетраэдр и додекаэдр
- 39. Упражнение 20 Найдите ребро додекаэдра, вписанного в единичный тетраэдр.
- 40. Скачать презентацию
- 41. Похожие презентации
Куб и тетраэдрТетраэдр можно вписать в куб так, что вершинами тетраэдра будут некоторые вершины куба.





















Слайд 2
Куб и тетраэдр
Тетраэдр можно вписать в куб так,
что вершинами тетраэдра будут некоторые вершины куба.
Слайд 4
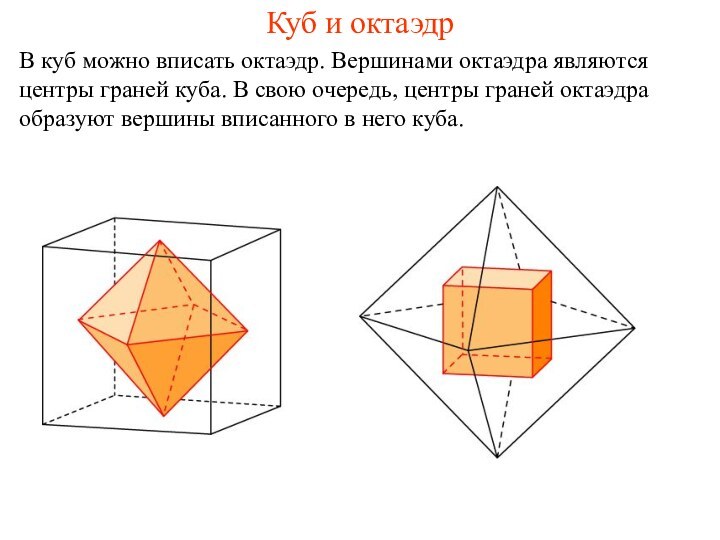
Куб и октаэдр
В куб можно вписать октаэдр. Вершинами
октаэдра являются центры граней куба. В свою очередь, центры
граней октаэдра образуют вершины вписанного в него куба.
Слайд 7
Куб и икосаэдр
В
куб можно вписать икосаэдр так, что серединами ребер икосаэдра
будут центры граней куба.
Слайд 8
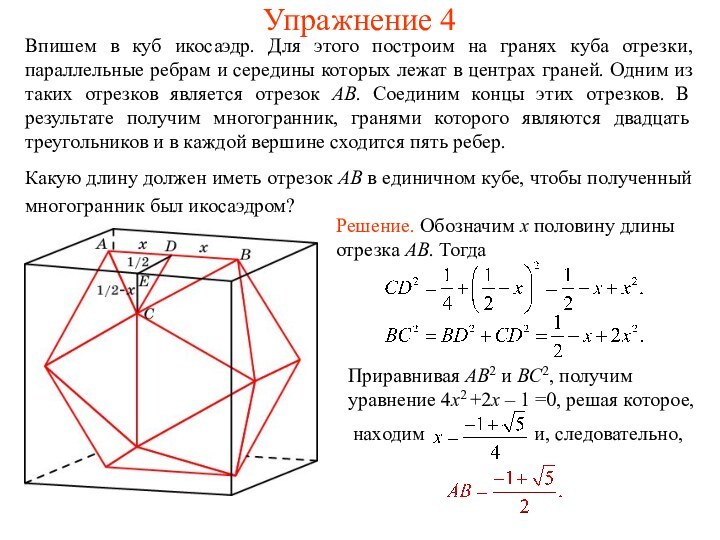
Упражнение 4
Впишем в куб икосаэдр. Для этого построим
на гранях куба отрезки, параллельные ребрам и середины которых
лежат в центрах граней. Одним из таких отрезков является отрезок AB. Соединим концы этих отрезков. В результате получим многогранник, гранями которого являются двадцать треугольников и в каждой вершине сходится пять ребер.Какую длину должен иметь отрезок AB в единичном кубе, чтобы полученный многогранник был икосаэдром?
Слайд 9
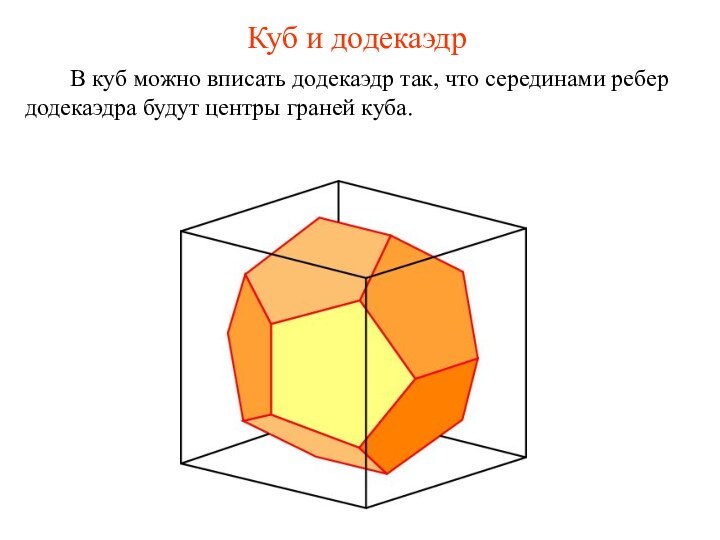
Куб и додекаэдр
В
куб можно вписать додекаэдр так, что серединами ребер додекаэдра
будут центры граней куба.
Слайд 10
Упражнение 5
Впишем в куб додекаэдр. Для этого построим
на гранях куба отрезки, параллельные ребрам и середины которых
лежат в центрах граней. Одним из таких отрезков является отрезок AB. Соединим концы этих отрезков. В результате получим многогранник, гранями которого являются двадцать треугольников и в каждой вершине сходится пять ребер.Какую длину должен иметь отрезок AB в единичном кубе, чтобы полученный многогранник был додекаэдром?
Слайд 11
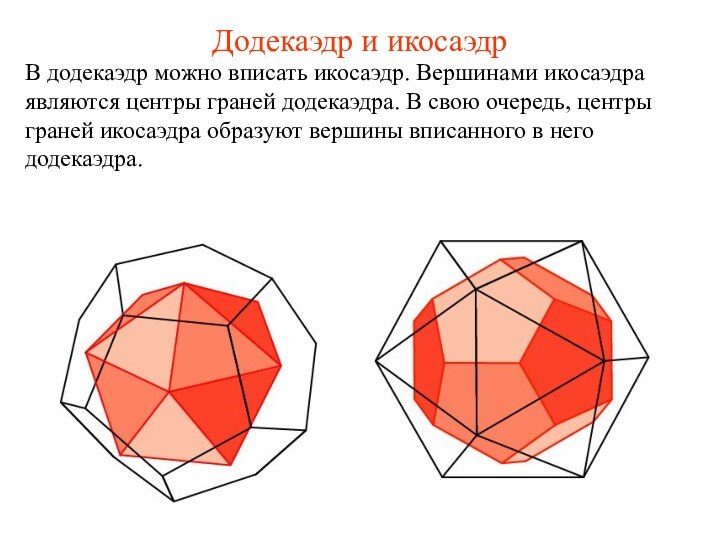
Додекаэдр и икосаэдр
В додекаэдр можно вписать икосаэдр. Вершинами
икосаэдра являются центры граней додекаэдра. В свою очередь, центры
граней икосаэдра образуют вершины вписанного в него додекаэдра.
Слайд 14
Додекаэдр и куб
Куб можно вписать в додекаэдр так,
что вершинами куба будут некоторые вершины додекаэдра.
Слайд 16
Додекаэдр и тетраэдр
В додекаэдр можно вписать куб так,
что вершинами куба будут некоторые вершины додекаэдра. Вписывая в
куб тетраэдр, получим тетраэдр, вписанный в додекаэдр. На рисунке ребра тетраэдра изображены зеленым цветом.
Слайд 18
Додекаэдр и октаэдр
Октаэдр
можно вписать в додекаэдр так, что вершинами октаэдра будут
середины ребер додекаэдра.Для этого сначала в куб вписываем октаэдр и додекаэдр. При этом октаэдр окажется вписанным в додекаэдр.
Слайд 20
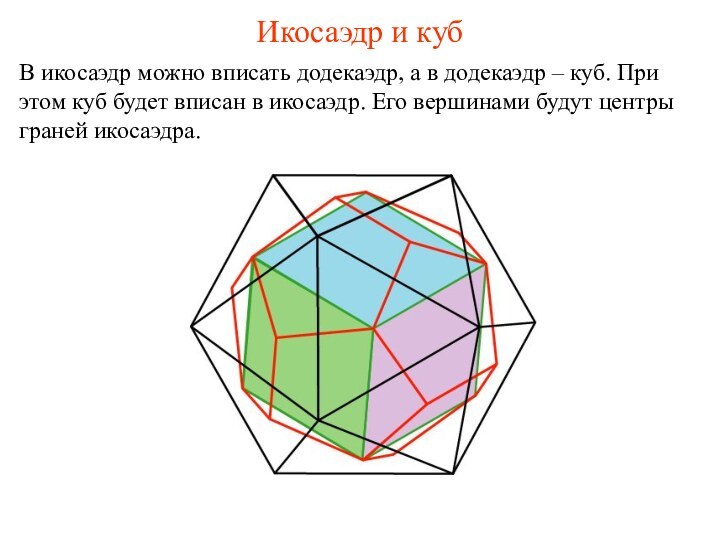
Икосаэдр и куб
В икосаэдр можно вписать додекаэдр, а
в додекаэдр – куб. При этом куб будет вписан
в икосаэдр. Его вершинами будут центры граней икосаэдра.
Слайд 22
Икосаэдр и тетраэдр
В икосаэдр можно вписать куб так,
что вершинами куба будут центры граней икосаэдра. Вписывая в
куб тетраэдр, получим тетраэдр, вписанный в икосаэдр. На рисунке ребра тетраэдра изображены зеленым цветом.
Слайд 24
Икосаэдр и октаэдр
Октаэдр
можно вписать в икосаэдр так, что вершинами октаэдра будут
середины ребер икосаэдра.Для этого сначала в куб вписываем октаэдр и икосаэдр. При этом октаэдр окажется вписанным в икосаэдр.
Слайд 26
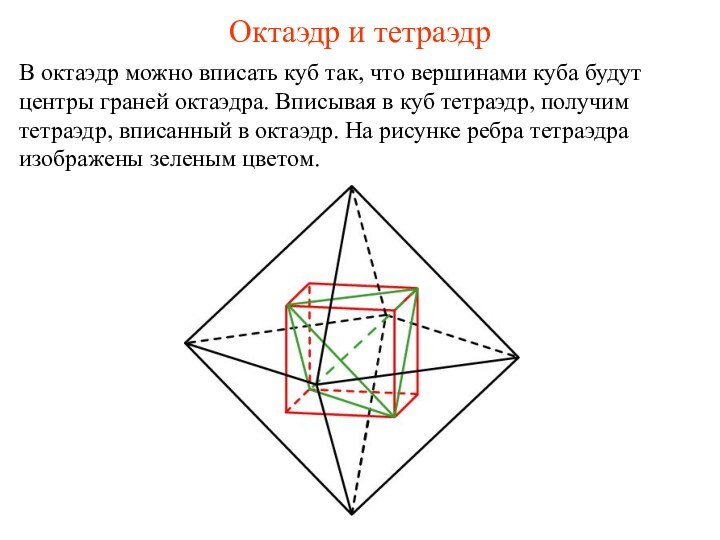
Октаэдр и тетраэдр
В октаэдр можно вписать куб так,
что вершинами куба будут центры граней октаэдра. Вписывая в
куб тетраэдр, получим тетраэдр, вписанный в октаэдр. На рисунке ребра тетраэдра изображены зеленым цветом.
Слайд 28
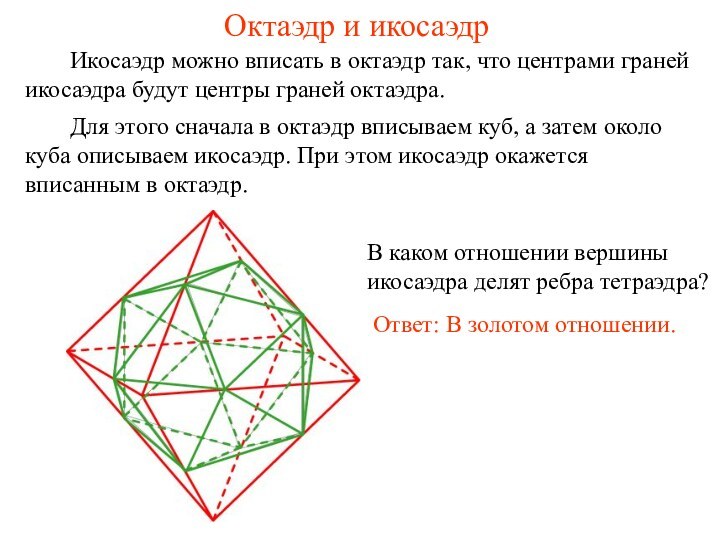
Октаэдр и икосаэдр
Икосаэдр
можно вписать в октаэдр так, что центрами граней икосаэдра
будут центры граней октаэдра.В каком отношении вершины икосаэдра делят ребра тетраэдра?
Ответ: В золотом отношении.





























