- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Решение теоремы Пифагора
Содержание
- 2. Биография ПифагораПисьменных документов о Пифагоре Самосском не
- 3. Пифагор и его последователи – пифагорейцы -
- 4. Пифагорейцы верили, что в числовых закономерностях спрятана
- 5. История теоремы
- 9. Формулировка теоремыПриведем различные формулировки теоремы Пифагора в
- 10. В Geometria Culmonensis (около 1400 г.) в
- 11. В настоящее время известно, что эта теорема
- 12. Верна, как и в его далекий век.
- 13. Простейшее доказательство
- 14. Доказательство методом дополнения
- 15. Поясним этот метод на примере. На рис.
- 16. Остается доказать, что наши шестиугольники равновелики. Заметим,
- 18. треугольники 1, 2, 3, 4; прямоугольник 5;
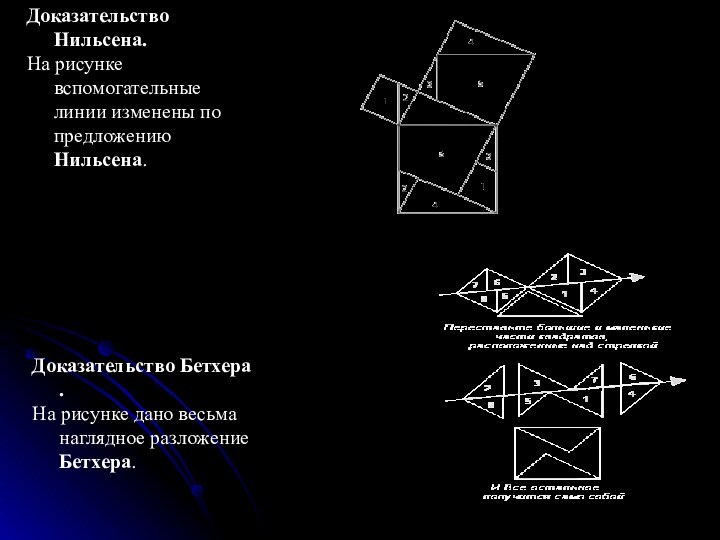
- 19. Доказательство методом разложенияСуществует целый ряд доказательств теоремы
- 25. Применение теоремыРассмотрим примеры практического применения теоремы Пифагора.
- 32. Т. к. она заключена между двумя концентрическими
- 34. У египтян была известна задача о лотосе.
- 36. Скачать презентацию
- 37. Похожие презентации
Биография ПифагораПисьменных документов о Пифагоре Самосском не осталось, а по более поздним свидетельствам трудно восстановить подлинную картину его жизни и достижений. Известно, что Пифагор покинул свой родной остров Самос в Эгейском море у берегов Малой Азии



































Слайд 3 Пифагор и его последователи – пифагорейцы - образовали
тайный союз, игравший немалую роль в жизни греческих колоний
в Италии. Пифагорейцы узнавали друг друга по звездчатому пятиугольнику – пентаграмме.На учение Пифагора большое влияние оказала философия и религия Востока. Он много путешествовал по странам Востока: был в Египте и в Вавилоне. Там Пифагор познакомился и с восточной математикой. Математика стала частью его ученья, и важнейшей его частью.
Слайд 4 Пифагорейцы верили, что в числовых закономерностях спрятана тайна
мира. Мир чисел жил для пифагорейца особой жизнью, числа
имели свой жизненный смысл. Числа, равные сумме своих делителей, воспринимались как совершенные (6, 28, 496, 8128); дружественными называли пары чисел, из которых каждое равнялось сумме делителей другого (например, 220 и 284). Пифагор впервые разделил числа на четные и нечетные, простые и составные, ввел понятие фигурного числа. Естественно, что геометрия у Пифагора была подчинена арифметике, это ярко проявилось в теореме, носящей его имя и ставшей в дальнейшем основой применения численных методов в геометрии.
Слайд 9
Формулировка теоремы
Приведем различные формулировки теоремы Пифагора в переводе
с греческого, латинского и немецкого языков.
У Евклида эта
теорема гласит (дословный перевод): "В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол".
Латинский перевод арабского текста Аннаирици (около 900 г. до н. э. ), сделанный Герхардом Клемонским (начало 12 в.), в переводе на русский гласит:
"Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол".
Слайд 10 В Geometria Culmonensis (около 1400 г.) в переводе
теорема читается так :
"Итак, площадь квадрата, измеренного по
длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу".В первом русском переводе евклидовых "Начал", сделанном Ф. И. Петрушевским, теорема Пифагора изложена так:
"В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол".
Слайд 11 В настоящее время известно, что эта теорема не
была открыта Пифагором. Однако одни полагают, что Пифагор первым
дал ее полноценное доказательство, а другие отказывают ему и в этой заслуге. Некоторые приписывают Пифагору доказательство, которое Евклид приводит в первой книге своих "Начал". С другой стороны, Прокл утверждает, что доказательство в "Началах" принадлежит самому Евклиду. Как мы видим, история математики почти не сохранила достоверных данных о жизни Пифагора и его математической деятельности. Зато легенда сообщает даже ближайшие обстоятельства, сопровождавшие открытие теоремы. Многим известен сонет Шамиссо:Пребудет вечной истина, как скоро Ее познает слабый человек! И ныне теорема Пифагора
Слайд 12 Верна, как и в его далекий век. Обильно было
жертвоприношенье Богам от Пифагора. Сто быков Он отдал на закланье и
сожженье За света луч, пришедший с облаков. Поэтому всегда с тех самых пор, Чуть истина рождается на свет, Быки ревут, ее почуя ,вслед. Они не в силах свету помешать , А могут лишь закрыв глаза дрожать От страха, что вселил в них Пифагор.Слайд 15 Поясним этот метод на примере. На рис. к
обычной пифагоровой фигуре приставлены сверху и снизу треугольники 2
и 3, равные исходному треугольнику 1. Прямая DG обязательно пройдет через C. Заметим теперь (далее мы это докажем), что шестиугольники DABGFE и CAJKHB равновелики. Если мы от первого из них отнимем треугольники 1 и 2, то останутся квадраты, построенные на катетах, а если от второго шестиугольника отнимем равные треугольники 1 и 3, то останется квадрат, построенный на гипотенузе. Отсюда вытекает, что квадрат, построенный на гипотенузе, равновелик сумме квадратов, построенных на катетах.Слайд 16 Остается доказать, что наши шестиугольники равновелики. Заметим, что
прямая DG делит верхний шестиугольник на равновеликие части; то
же можно сказать о прямой CK и нижнем шестиугольнике. Повернем четырехугольник DABG, составляющий половину шестиугольника DABGFE, вокруг точки А по часовой стрелке на угол 90; тогда он совпадет с четырехугольником CAJK, составляющим половину шестиугольника CAJKHB. Поэтому шестиугольники DABGFE и CAJKHB равновелики
Слайд 18
треугольники 1, 2, 3, 4;
прямоугольник 5;
прямоугольник
6 и квадрат 8;
прямоугольник 7 и квадрат 9;
Затем выбросим из прямоугольника части так, чтобы остались только квадраты, построенные на катетах. Этими частями будут:
прямоугольники 6 и 7;
прямоугольник 5;
прямоугольник 1(заштрихован);
прямоугольник 2(заштрихован);
Нам осталось лишь показать, что отнятые части равновелики. Это легко видеть в силу расположения фигур. Из рисунка ясно, что:
прямоугольник 5 равновелик самому себе;
четыре треугольника 1,2,3,4 равновелики двум прямоугольникам 6 и 7;
прямоугольник 6 и квадрат 8, взятые вместе, равновелики прямоугольнику 1 (заштрихован);;
прямоугольник 7 вместе с квадратом 9 равновелики прямоугольнику 2(заштрихован);
Доказательство закончено.
Слайд 19
Доказательство методом разложения
Существует целый ряд доказательств теоремы Пифагора,
в которых квадраты, построенные на катетах и на гипотенузе,
разрезаются так, что каждой части квадрата ,построенного на гипотенузе, соответствует часть одного из квадратов, построенных на катетах. Во всех этих случаях для понимания доказательства достаточно одного взгляда на чертеж; рассуждение здесь может быть ограничено единственным словом: "Смотри!", как это делалось в сочинениях древних индусских математиков. Следует, однако, заметить, что на самом деле доказательство нельзя считать полным, пока мы не доказали равенства всех соответствующих друг другу частей. Это почти всегда довольно не трудно сделать, однако может (особенно при большом количестве частей) потребовать довольно продолжительной работы.
Слайд 25
Применение теоремы
Рассмотрим примеры практического применения теоремы Пифагора. Не
будем пытаться привести все примеры использования теоремы - это
вряд ли было бы возможно. Область применения теоремы достаточно обширна и вообще не может быть указана с достаточной полнотой. Определим возможности, которые дает теорема Пифагора для вычисления длин отрезков некоторых фигур на плоскости.Слайд 32 Т. к. она заключена между двумя концентрическими окружностями,
то ее диаметр равен расстоянию между этими окружностями, т.
е. b/2 и, следовательно, радиус равен b/4. А тогда становится ясным и положение ее центра.В рассмотренном примере радиусы находились без всяких затруднений. В других аналогичных примерах могут потребоваться вычисления; покажем, как применяется в таких задачах теорема Пифагора.