Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Площади многоугольников

Содержание

Площади многоугольников
Геометрия Площади многоугольников Площадь многоугольника.Основные свойства площадей.Площадь прямоугольника.Площадь параллелограмма.Площадь треугольника.Площадь трапеции.Площадь ромба.Содержание Площадь многоугольникаЕдиницей измерения площадей является квадрат со стороной равной единице измерения отрезков.S=1см2 Основные свойства площадей - Равные многоугольники имеют равные площади. Площадь прямоугольникаПлощадь прямоугольника равна abABCDпроизведению его смежных сторон Площадь параллелограммаПлощадь параллелограмм равнаCaBDhAпроизведению его основания на высоту. Площадь треугольникаПлощадь треугольника равна половине произведения его основания ABCahна высоту. Площадь треугольникаПлощадь треугольника можно вычислить по формуле ГеронаABCacb Площадь треугольникаПлощадь равностороннего треугольника aaABCвычисляется по формулеa Площадь треугольникаСледствие 1. Площадь прямоугольного треугольника равна произведения его катетов.Следствие 2. Если Площадь треугольникаЕсли угол одного треугольника ss1равенуглу другого треугольника, то относятся как произведения Площадь трапеции.Площадь трапеции равна произведению полусуммы ее основанийABCDbahна высоту. Площадь трапеции.Площадь трапеции равна ABCDEFhпроизведению средней линиина высоту. Площадь ромба.Площадь ромба равна ABCDd1d2половине произведения его диагоналей.
Слайды презентации

Слайд 2 Площади многоугольников

Площади многоугольников

Слайд 3 Площадь многоугольника.
Основные свойства площадей.
Площадь прямоугольника.
Площадь параллелограмма.
Площадь треугольника.
Площадь трапеции.
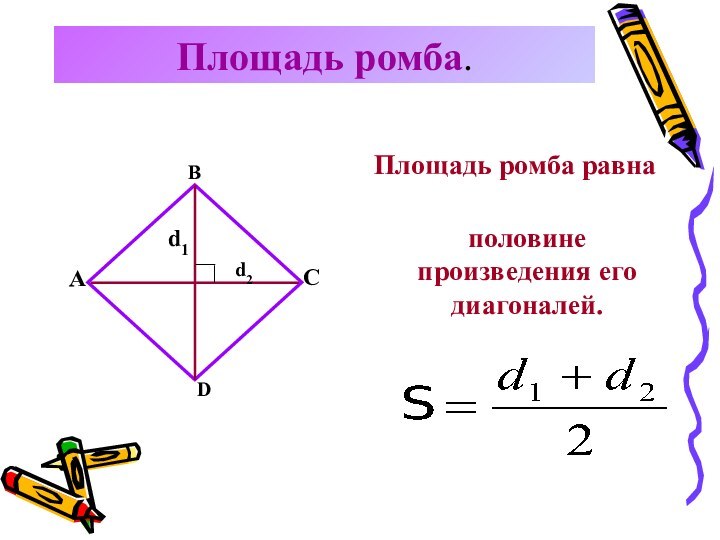
Площадь

Площадь многоугольника.Основные свойства площадей.Площадь прямоугольника.Площадь параллелограмма.Площадь треугольника.Площадь трапеции.Площадь ромба.Содержание

ромба.

Содержание

Слайд 4 Площадь многоугольника
Единицей измерения площадей является квадрат со стороной

Площадь многоугольникаЕдиницей измерения площадей является квадрат со стороной равной единице измерения отрезков.S=1см2

равной единице измерения отрезков.
S=1см2

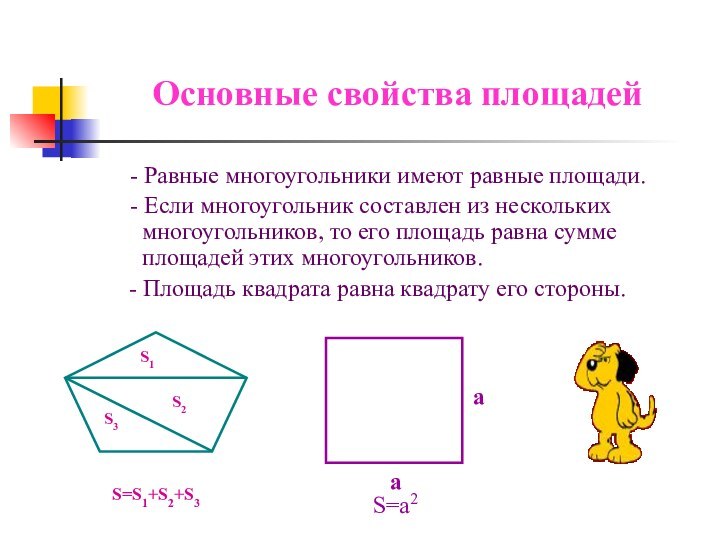
Слайд 5 Основные свойства площадей
- Равные многоугольники

Основные свойства площадей - Равные многоугольники имеют равные площади.

имеют равные площади.
- Если многоугольник составлен

из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.


S=S1+S2+S3

S=a2

- Площадь квадрата равна квадрату его стороны.

Слайд 6 Площадь прямоугольника
Площадь прямоугольника равна



a
b
A
B
C
D
произведению его смежных сторон

Площадь прямоугольникаПлощадь прямоугольника равна abABCDпроизведению его смежных сторон

Слайд 7 Площадь параллелограмма
Площадь параллелограмм равна
C
a

B
D
h
A
произведению его основания
на высоту.

Площадь параллелограммаПлощадь параллелограмм равнаCaBDhAпроизведению его основания на высоту.

Слайд 8 Площадь треугольника
Площадь треугольника равна половине произведения его основания

Площадь треугольникаПлощадь треугольника равна половине произведения его основания ABCahна высоту.



A
B
C
a
h
на высоту.

Слайд 9 Площадь треугольника
Площадь треугольника можно вычислить по формуле Герона
A
B
C
a
c
b

Площадь треугольникаПлощадь треугольника можно вычислить по формуле ГеронаABCacb

Слайд 10 Площадь треугольника
Площадь равностороннего треугольника

a
a
A
B
C
вычисляется по формуле
a

Площадь треугольникаПлощадь равностороннего треугольника aaABCвычисляется по формулеa

Слайд 11 Площадь треугольника
Следствие 1. Площадь прямоугольного треугольника равна произведения

Площадь треугольникаСледствие 1. Площадь прямоугольного треугольника равна произведения его катетов.Следствие 2.

его катетов.
Следствие 2. Если высоты двух треугольников равны, то

их площади относятся как основания.

Слайд 12 Площадь треугольника
Если угол одного треугольника
s

s1
равен
углу другого треугольника,

Площадь треугольникаЕсли угол одного треугольника ss1равенуглу другого треугольника, то относятся как

то
относятся как произведения

сторон, заключающих равные углы.

площади этих треугольников

Слайд 13 Площадь трапеции.
Площадь трапеции равна произведению полусуммы ее оснований

A
B
C
D
b
a
h
на

Площадь трапеции.Площадь трапеции равна произведению полусуммы ее основанийABCDbahна высоту.

высоту.

Слайд 14 Площадь трапеции.
Площадь трапеции равна

A

B
C
D

E
F
h
произведению средней линии
на высоту.

Площадь трапеции.Площадь трапеции равна ABCDEFhпроизведению средней линиина высоту.
  • Имя файла: ploshchadi-mnogougolnikov.pptx
  • Количество просмотров: 164
  • Количество скачиваний: 0
- Предыдущая Рубенс, Питер Пауль
Следующая - Фокина Л. П. Шаблон презентации 1

Похожие презентации

Презентация по геометрии 9 класс на тему: Решение треугольников. Презентация по геометрии 9 класс на тему: Решение треугольников. 148
Презентация урока по геометрии Треугольники 7 класс Презентация урока по геометрии Треугольники 7 класс 143
Точка, прямая, отрезок, луч и угол Точка, прямая, отрезок, луч и угол 156
Презентация Аксиомы стереометрии (10 класс) Презентация Аксиомы стереометрии (10 класс) 156
Симметрия вокруг нас - презентация к уроку. Удобный шаблон презентации для скрытых слайдов Симметрия вокруг нас - презентация к уроку. Удобный шаблон презентации для скрытых слайдов 183
Презентация по математике Теорема Пифагора (8 класс) Презентация по математике Теорема Пифагора (8 класс) 150
Презентация по геометрии на тему Аксиомы геометрии Презентация по геометрии на тему Аксиомы геометрии 153
Орнамент Орнамент 152
Окружность и круг Окружность и круг 168
Начальные геометрические сведенья Начальные геометрические сведенья 252
Ромб Ромб 137
Площадь многоугольника Площадь многоугольника 120
Осевая симметрия в геометрии Осевая симметрия в геометрии 175
Пересечение геометрических фигур Пересечение геометрических фигур 219
Практическое применение подобия треугольников Практическое применение подобия треугольников 188
Центральная и осевая симметрия Центральная и осевая симметрия 155
Парабола и параболические антенны Парабола и параболические антенны 154
Многоугольники Многоугольники 165
Изготовление набора для решения задач с пространственными телами Изготовление набора для решения задач с пространственными телами 155
наглядная геометрия наглядная геометрия 154
Теорема синусов и косинусов Теорема синусов и косинусов 170
Сечения, разрезы, их виды и применение Сечения, разрезы, их виды и применение 214
Задачи практического содержания на нахождение объемов пространственных тел. Задачи практического содержания на нахождение объемов пространственных тел. 183
Справочное пособие по геометрии - 7 класс Справочное пособие по геометрии - 7 класс 182
Алгебра и геометрия Алгебра и геометрия 148
Геометрия в древности Геометрия в древности 166
Решение задач по геометрии. Подгоовка к ЕГЭ. Базовый уровень. Решение задач по геометрии. Подгоовка к ЕГЭ. Базовый уровень. 191
Оптимизированный подход в составлении карточек-заданий по черчению Оптимизированный подход в составлении карточек-заданий по черчению 143
Цилиндр Цилиндр 157
Отрезки Отрезки 143