Слайд 2
ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
Стереометрия – (от греч. «стереос»- «объемный»,
«пространственный») раздел геометрии, изучающий форму, размеры и взаимное расположение
пространственных фигур.
Аксиомы стереометрии
1.) Аксиома выхода в пространство
2.)Аксиома плоскости
3.)Аксиома прямой
4.)Аксиома пересечения плоскостей
Слайд 3
АКСИОМА ВЫХОДА В ПРОСТРАНСТВО
Аксиома : имеются 4 точки,
не лежащие в одной плоскости.
Слайд 4
АКСИОМА ПЛОСКОСТИ
Аксиома : через любые три точки, не
лежащие на одной прямой, проходит плоскость, притом только одна.
Слайд 5
АКСИОМА ПРЯМОЙ
Аксиома прямой : через любые две точки
на плоскости можно провести только одну прямую.
Слайд 6
АКСИОМА ПЕРЕСЕЧЕНИЯ ПЛОСКОСТЕЙ
Аксиома : если две плоскости имеют
общую точку, то их пересечением есть прямая, содержащая все
общие точки.
Слайд 7
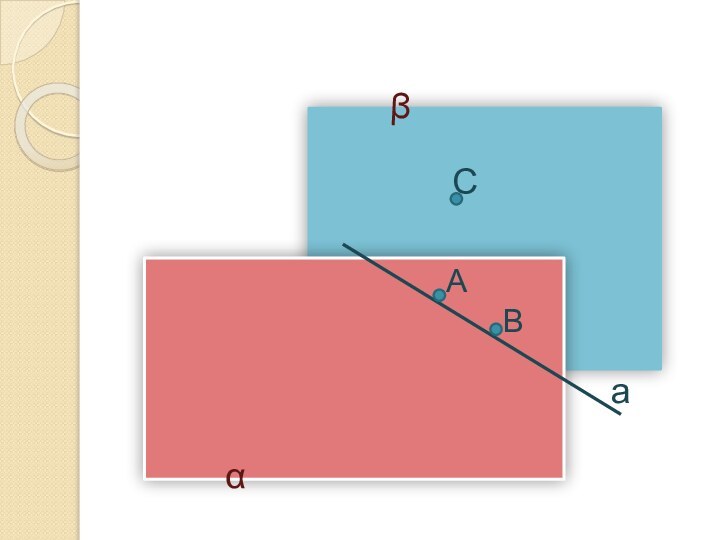
СЛЕДСТВИЕ ИЗ АКСИОМЫ
10. Прямая, имеющая с плоскостью хотя
бы две общие точки, целиком лежит в этой плоскости.
Дано:α, А α, В α,
а, А а, В а.
Доказать: а α
Доказательство:
Слайд 9
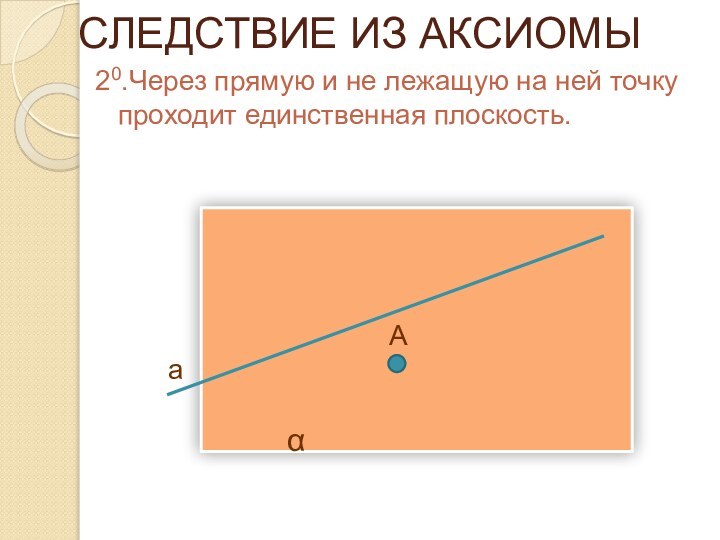
СЛЕДСТВИЕ ИЗ АКСИОМЫ
20.Через прямую и не лежащую на
ней точку проходит единственная плоскость.
Слайд 10
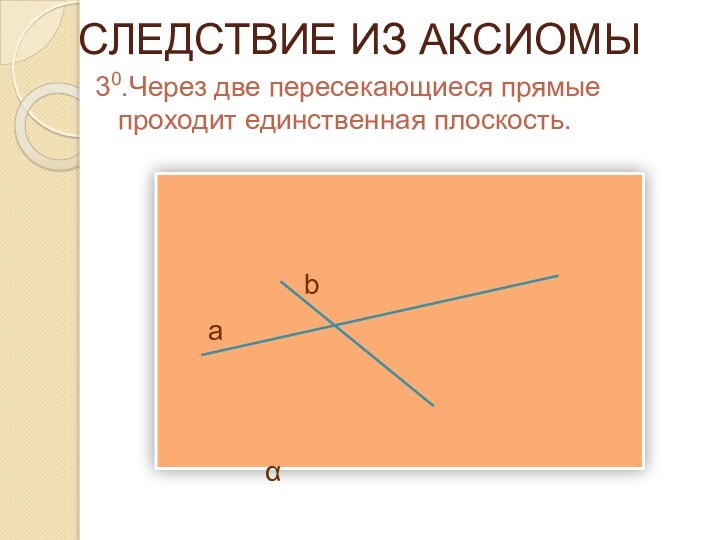
СЛЕДСТВИЕ ИЗ АКСИОМЫ
30.Через две пересекающиеся прямые проходит единственная
плоскость.
Слайд 11
ПРЯМЫЕ. ПЛОСКОСТИ. ПАРАЛЛЕЛЬНОСТЬ
Опред.: две прямые в пространстве называются
параллельными, если они лежат в одной плоскости и не
имеют общих точек.
Слайд 12
СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ
1)Через точку, не лежащую на данной
прямой, можно провести единственную прямую, параллельную данной.
Слайд 13
СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ
2)Если две прямые параллельны третьей, то
они параллельны друг другу.
Слайд 14
3)Если одна из двух параллельных прямых пересекает плоскость,
то и вторая прямая обязана ее пересечь.
СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ
Слайд 15
ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
Опред.: прямая и плоскость называются
параллельными, если они не имеют общих точек.
Слайд 16
ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМОЙ И ПЛОСКОСТИ
Теорема : Если прямая,
не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей
в этой плоскости, то она параллельна данной плоскости.
Слайд 17
СЛЕДСТВИЕ ИЗ ТЕОРЕМЫ
10.Если плоскость проходит через данную прямую.
Параллельную другой плоскости, и пересекают эту плоскость, то линия
пересечения плоскостей параллельна данной прямой.
Слайд 18
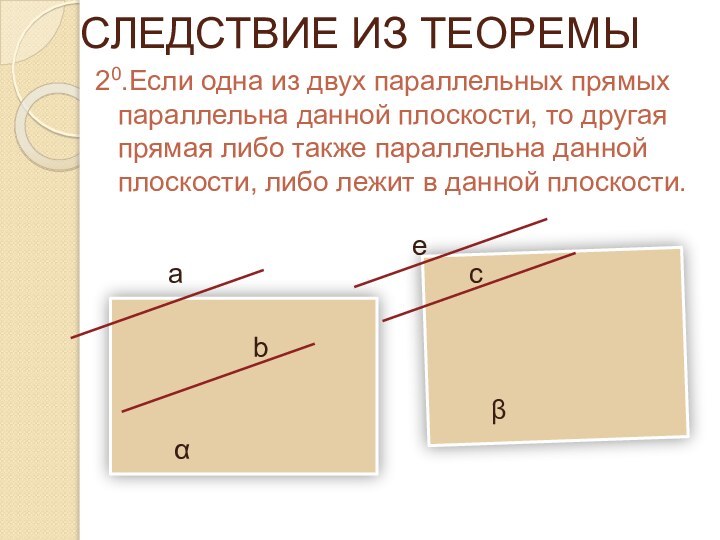
СЛЕДСТВИЕ ИЗ ТЕОРЕМЫ
20.Если одна из двух параллельных прямых
параллельна данной плоскости, то другая прямая либо также параллельна
данной плоскости, либо лежит в данной плоскости.
Слайд 19
СЛЕДСТВИЕ ИЗ ТЕОРЕМЫ
30. Если плоскость и прямая, не
лежащая в данной плоскости, параллельны некоторой прямой, также не
лежащей в данной плоскости, (или плоскости) то они параллельны друг другу.
Слайд 20
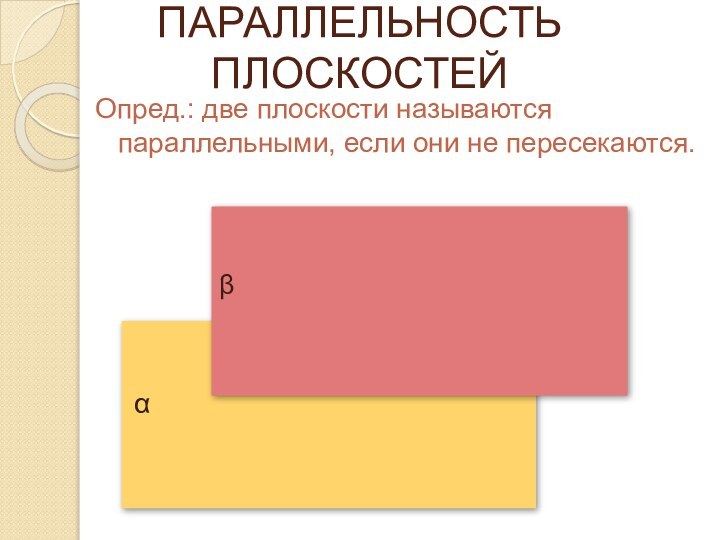
ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ
Опред.: две плоскости называются параллельными, если они
не пересекаются.
Слайд 21
ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ДВУХ ПЛОСКОСТЕЙ
Теорема : Если две пересекающиеся
прямые в одной плоскости соответственно параллельны двум пересекающимся прямым
в другой плоскости, то эти плоскости параллельны.
Слайд 22
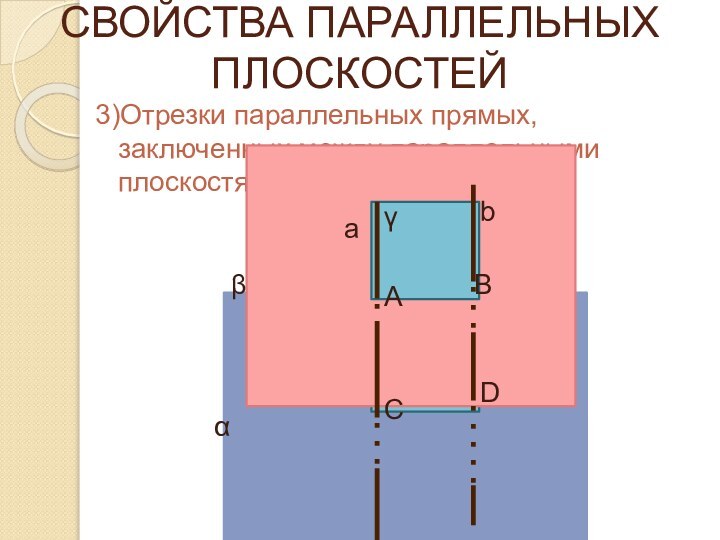
СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЕЙ
1)Если две параллельные плоскости пересечены третьей,
то линии их пересечения параллельны.
Слайд 23
СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЕЙ
2)Если две плоскости параллельны третьей плоскости,
то они параллельны и между собой.