- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Метод золотого сечения
Содержание
- 2. Золотая пропорция – гармония и красотаВыполнили
- 3. Гармоничны ли люди?Гармония( по-гречески harmonia) образовано от
- 4. гипотезаМы считаем, что человек и все вокруг подчиняется принципу гармонии – принципу пропорции.
- 5. Наши задачи:Познакомиться с золотой пропорцией и связанных
- 6. Принцип гармонииГармония есть «согласие разногласного». В гармонии заложена изначальная противоречивость мира.
- 7. «Золотая пропорция» в человекеЦели исследования:-Изучить разнообразие применения
- 8. История золотого сеченияПринято считать, что понятие о золотом делении ввел в научный обиход Пифагор
- 9. ϕ= 0,618 = 5/8Золотое сечение – это
- 10. Построение шкалы отрезков золотой пропорции Если на
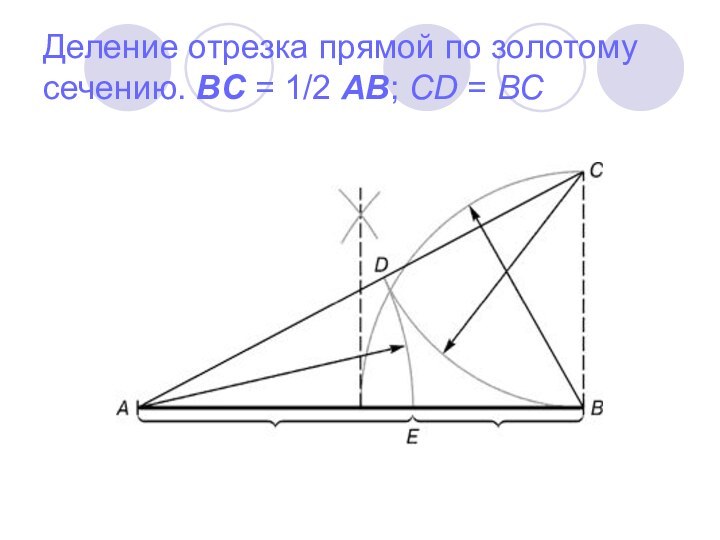
- 11. Деление отрезка прямой по золотому сечению. BC = 1/2 AB; CD = BC
- 12. Золотая спиральЕсли этот процесс продолжить, то получим
- 13. Золотой прямоугольникЗолотой прямоугольник обладает многими интересными свойствами.
- 14. Пятиконечная звездаПятиконечная звезда, получаемая при последовательном соединении
- 15. Золотое сечение в математикеС историей золотого сечения
- 16. Золотое сечение в математикеРяд чисел 0, 1,
- 17. Русский архитектор М.Ф. Казаков широко использовал в
- 18. Пропорциональность в природе, искусстве, архитектуре означает соблюдение
- 19. Золотое сечение в архитектуре
- 20. Золотое сечение в скульптуреСкульптор и теоретик искусства
- 21. Золотое сечение в скульптуреШирокие плечи почти равны
- 22. Золотое сечение в искусстве
- 23. Золотая спираль в искусствеЕсли золотой прямоугольник использовался
- 24. Золотое сечение в живописиМотивы золотого сечения просматриваются
- 25. Золотое сечение в живописиХолст, на котором написана
- 26. Золотое сечение в фотографииНа протяжении многих веков,
- 27. В портретной съемке (или съемке человека), где,
- 28. Правило золотого сечения вполне применимо и к
- 29. Тот же самый прием будет
- 30. При съемке натюрмортов и различных «макросюжетов» природы,
- 31. Композиционное правило золотого сечения позволит улучшить качество
- 32. Золотая спираль в природеВ природе золотую спираль
- 33. Золотое сечение в природеЗдесь золотое сечение проявляется
- 34. Золотое сечение в природеРассматривая расположение
- 35. Золотое сечение в теле человекаЗолотое сечение заложено
- 36. Золотая пропорция в человеческом теле
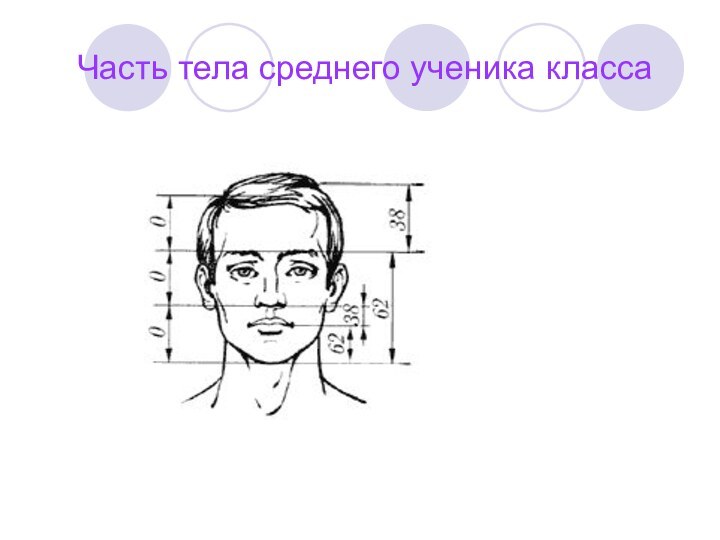
- 37. Часть тела среднего ученика класса
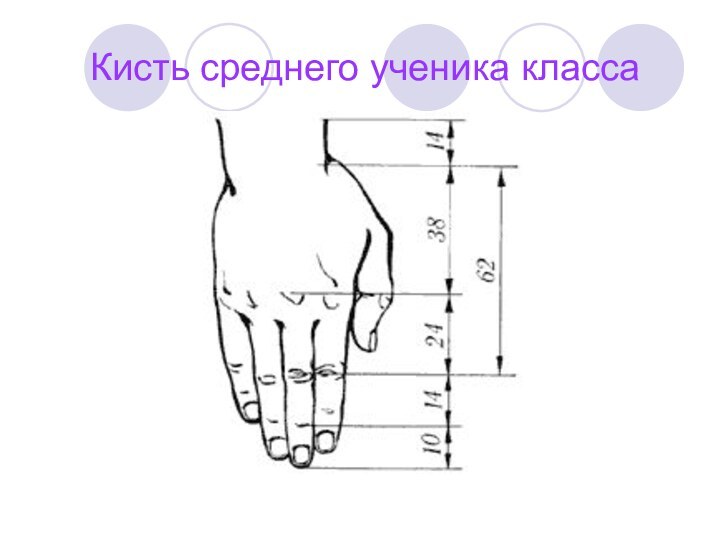
- 38. Кисть среднего ученика класса
- 39. http://www.trinitas.ru/Геометрия: красота и гармония. Простейшие задачи аналитической
- 40. Ссылки http://www.goldenmuseum.com/
- 41. Скачать презентацию
- 42. Похожие презентации
Золотая пропорция – гармония и красотаВыполнили учащиеся 9 класса: Ларина Екатерина, Морозов Дмитрий, Кочеткова Яна, Петрович Денис и др.




































Слайд 3
Гармоничны ли люди?
Гармония( по-гречески harmonia) образовано от слова
harmozo – приводить в порядок.
Золотое сечение – гармоническая пропорция.
Пропорция- т.к. здесь участвуют два равных отношения. А гармоническая - создающая гармонию, приятные для глаза впечатления.
Слайд 4
гипотеза
Мы считаем, что человек и все вокруг подчиняется
принципу гармонии – принципу пропорции.
Слайд 5
Наши задачи:
Познакомиться с золотой пропорцией и связанных с
нею отношений
Изучить применение золотой пропорции в архитектуре, искусстве
Познакомиться с
золотой пропорцией и связанных с нею отношений, наблюдаемых в живой природе
Слайд 6
Принцип гармонии
Гармония есть «согласие разногласного».
В гармонии заложена
изначальная
противоречивость мира.
Слайд 7
«Золотая пропорция» в человеке
Цели исследования:
-Изучить разнообразие применения золотого
сечения и связанные с ним соотношения в реальной жизни
-
Разобраться в пропорциях человека, фотографии как гармонии и красоты
Слайд 8
История золотого сечения
Принято считать, что понятие о золотом
делении ввел в научный обиход Пифагор
Слайд 9
ϕ= 0,618 = 5/8
Золотое сечение – это деление
отрезка, при котором длина всего отрезка так относится к
длине его большей части, как длина большей части к меньшей.Это отношение обозначают буквой ϕ;
С этими пропорциями связывались представления о красоте, порядке и гармонии, о созвучных аккордах в музыке.
Определение
Слайд 10
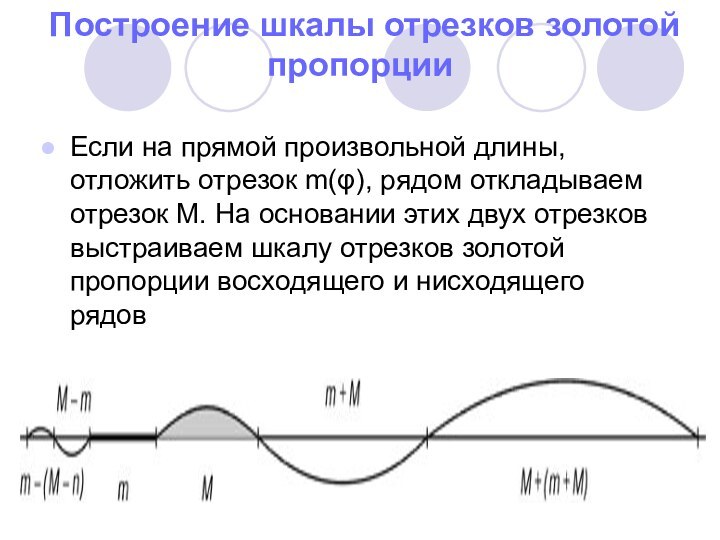
Построение шкалы отрезков золотой пропорции
Если на прямой произвольной
длины, отложить отрезок m(φ), рядом откладываем отрезок M. На
основании этих двух отрезков выстраиваем шкалу отрезков золотой пропорции восходящего и нисходящего рядов
Слайд 12
Золотая спираль
Если этот процесс продолжить, то получим «вращающиеся
квадраты». Когда соединим их вершины плавной кривой, то получим
золотую спираль.
Слайд 13
Золотой прямоугольник
Золотой прямоугольник обладает многими интересными свойствами. Если,
например, от золотого прямоугольника АВСD отрезать квадрат со стороной,
равной меньшей стороне прямоугольника, то снова получим золотой прямоугольник EFCD и т.д.
Слайд 14
Пятиконечная звезда
Пятиконечная звезда, получаемая при последовательном соединении через
одну всех вершин правильного пятиугольника (пентаграмма), всегда привлекала внимание
людей совершенством формы. Пифагорейцы именно ее выбрали символом своего союза. В этой фигуре наблюдается удивительное постоянство отношений составляющих ее отрезков.На рисунке AD:AC = AC:CD = AB:BC = AD:AE = AE:EC. Пользуясь симметрией звезды, этот ряд равенств можно продолжить. Все эти отношения равны числу Ф (1,618...).
Слайд 15
Золотое сечение в математике
С историей золотого сечения косвенным
образом связано имя итальянского математика монаха Леонардо из Пизы,
более известного под именем Фибоначчи (сын Боначчи).
Слайд 16
Золотое сечение в математике
Ряд чисел 0, 1, 1,
2, 3, 5, 8, 13, 21, 34, 55 и
т.д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а 34 : 55 = 0,618. Это отношение обозначается символом Ф. Только это отношение – 0,618 : 0,382 – дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему.Слайд 17 Русский архитектор М.Ф. Казаков широко использовал в своем
творчестве золотое сечение.
Здание бывшего Сената в
Кремле.Золотое сечение в архитектуре
Слайд 18 Пропорциональность в природе, искусстве, архитектуре означает соблюдение определенных
соотношений между размерами отдельных частей растения, скульптуры, здания и
является непременным условием правильного и красивого изображения предмета.Скульпторы, архитекторы, художники используют золотое сечение в своих произведениях.
К примеру, в храме Парфенон в Афинах отношение высоты здания к его длине равно ϕ.
Золотое сечение в архитектуре
Слайд 20
Золотое сечение в скульптуре
Скульптор и теоретик искусства Поликлет
в своем трактате "Канон" установил законы пропорциональности человеческого тела.
Так, пупок делит рост человека в отношении золотого сечения.Немецкий профессор Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон.
Греческий скульптор Леохар создал знаменитую статую Аполлона Бельведерского, воплотившую представление древних греков о красоте. Если высоту статуи разделить в отношении золотого сечения и то же самое проделать с каждой частью, то точки деления придутся на талию, каленную чашечку, адамово яблоко. Та же закономерность распространяется в отдельности на лицо, руку, кисть.
Слайд 21
Золотое сечение в скульптуре
Широкие плечи почти равны высоте
туловища, половина высоты тела приходится на лонное сращение, высота
головы 8 раз укладывается в высоте тела, а золотой пропорции отве-чает положение
пупка на теле
атлета
Гений Микеланджело - в его абсолютном понимании человеческого тела и пропорций его воспроизведения. Примером может служить знаменитая статуя - "Давид".
Слайд 23
Золотая спираль в искусстве
Если золотой прямоугольник использовался художниками
для создания у зрителя ощущения покоя, уравновешенности, то золотая
спираль, напротив, применялась для выражения тревоги, бурных событий.«Избиение младенцев»
Рафаэль, 1509 г.
Слайд 24
Золотое сечение в живописи
Мотивы золотого сечения просматриваются в
картинах Рафаэля:
Афинская школа Бракосочетание
святой девы
Слайд 25
Золотое сечение в живописи
Холст, на котором написана «Тайная
вечеря» Сальвадора Дали, имеет форму золотого прямоугольника, стороны которого
находятся в золотом отношении.«Тайная вечеря» С. Дали
Слайд 26
Золотое сечение в фотографии
На протяжении многих веков, для
построения гармоничных композиций художники пользуются понятием "Золотого сечения".
На
основе данного правила существуют различные способы построения гармоничных композиций, в том числе и в фотографии.Примером использования правила "Золотого сечения" может быть расположение основных компонентов кадра в особых точках - зрительных центрах, Таких точек всего четыре, и расположены они на расстоянии 3/8 и 5/8 от соответствующих краев плоскости. Человек всегда акцентирует свое внимание на
этих точках, независимо от формата
кадра или картины.
Слайд 27 В портретной съемке (или съемке человека), где, как
правило, важно сделать акцент на глаза, композиция выиграет, если
их расположить как можно ближе к пересечению этих линий.Изображение объекта в соответствии с правилом "золотого сечения" используется в виде классических приемов построения композиции. Например, объект, являющийся «центральной» фигурой кадра далеко не всегда должен быть расположен действительно в центре. Композиция будет смотреться выигрышней, если его расположить ближе к пересечению линий разметки.
Портретная съемка
Слайд 28
Правило золотого сечения вполне применимо и к портретам.
Мысленно
разделите кадр на девять частей.
После этого выстройте композицию кадра
так, чтобы один глаз человека находился на пересечении линий.Такой снимок будет производить более сильное впечатление, выглядеть эстетично.
Портретная съемка
Слайд 29 Тот же самый прием будет
«работать» для самых различных сюжетов съемки. В том числе для макросъемки.
Пейзажная фотография
Слайд 30 При съемке натюрмортов и различных «макросюжетов» природы, кадр
смотрится выигрышней, если разместить
композицию или объект не в центре кадра, а вдоль прямых и на точках их пересечения.Пейзажная фотография
Слайд 31
Композиционное правило золотого сечения позволит улучшить качество снимков.
Принцип
прост. Разделите изображение на 9 равных частей.
Наиболее эффектно смотрится
изображение, где основной объект находится на одном из пересечений линий. Совместив горизонт с одной из линий, вы получите гораздо более сильную композицию.Пейзажная фотография
Слайд 32
Золотая спираль в природе
В природе золотую спираль представляют
раковины многих моллюсков, улиток, а также рога архаров закручиваются
по золотой спирали.Паук эпейра сплетает паутину по золотой спирали.
Слайд 33
Золотое сечение в природе
Здесь золотое сечение проявляется в
пропорциях частей перпендикулярно к направлению роста.
В ящерице с
первого взгляда улавливаются приятные для нашего глаза пропорции – длина ее хвоста так относится к длине остального тела, как 62 к 38. Природа осуществила деление на симметричные части и золотые пропорции. В частях проявляется повторение строения целого.
Слайд 34
Золотое сечение в природе
Рассматривая расположение
листьев на стебле растений можно
заметить, что между
каждыми двумя парами листьев (А и С) третья рас-
положена в месте золотого
сечения (В).
Если первый отросток принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции
Слайд 35
Золотое сечение в теле человека
Золотое сечение заложено в
пропорциях человеческого тела.
Примером является статуя
Зевса Олимпийского (одно из семи чудес света).
Слайд 39
http://www.trinitas.ru/
Геометрия: красота и гармония. Простейшие задачи аналитической геометрии
на плоскости. Золотая пропорция. Симметрия вокруг нас. 8-9 классы:
элективные курсы/авт.-сост. Л.С. Сагателова, В.Н. Студенецкая. – Волгоград: Учитель, 2007. – 158с.Математика: наглядная геометрия: учеб. Для учащихся 6 кл.общеобразова. учреждений/ Т.Г. Ходот ,А.Ю.Ходот. – М.: Просвещение, 2007. – 143с.
http://gs.edunet.uz/viskust.htm
http://photoportal.kiev.ua/?lang_id=1&menu_id=1
http://www.dc-market.ru/about.htm
http://inoyrazum.narod.ru/pyramid.html
http://www.abc-people.com/idea/zolotsech/
http://www.abc-people.com/data/leonardov/pic_z-8.jpg
http://al-signa.narod.ru/lib/red/152.files/image014.gif
Ссылки