Слайд 2
Содержание
Общий исторический обзор
О
развитии геометрии в Древней
Греции до Евклида
Многогранники
Площадь поверхности призмы
Призма и пирамида
Измерение объемов
О пирамиде и её объеме
О призме и параллелепипеде
Параллелепипед
Слайд 3
Общий исторический обзор
Разные формы материальных тел наблюдал человек
в природе: формы растений и животных, гор и извилин
рек, круга и серпа Луны и т. п.
Слайд 4
Начало геометрии было положено в древности
при решении чисто практических задач. Со временем, когда накопилось
большое количество геометрических фактов, у людей появилось потребность обобщения, уяснения зависимости одних элементов от других, установления логических связей и доказательств. Постепенно создавалась геометрическая наука.
Слайд 5
Геометрические знания примерно в объеме современного курса средней
школы были изложены еще 2200 лет назад в “Началах”
Евклида. Конечно, изложенная в “Началах” наука геометрия не могла быть создана одним ученым. Известно, что Евклид в своей работе опирался на труды десятков предшественников, среди которых были Фалес и Пифагор, Демокрит и Гиппократ, Архит, Теэтет, Евдокс и др.
Пифагор
Демокрит
Гиппократ
Слайд 6
Ценой больших усилий, исходя из отдельных геометрических сведений,
накопленных тысячелетиями в практической деятельности людей, эти великие ученые
сумели на протяжении 3 - 4 столетий привести геометрическую науку к высокой ступени совершенства. Историческая заслуга Евклида состоит в том, что он, создавая свои “Начала”, объединил результаты своих предшественников, упорядочил и привел в одну систему основные геометрические знания того времени.
Евдокс
Слайд 7
Многие учебники элементарной геометрии
во всем мире представляли (а многие и поныне представляют)
собой лишь переработку книги Евклида. “Начала” на протяжении веков были настольной книгой величайших ученых. В XVII в. Декарт благодаря методу координат сделал возможным изучение свойств геометрических фигур с помощью алгебры. С этого времени начала развиваться аналитическая геометрия.
Коренной перелом в геометрии впервые произвел в первой половине ХIХ в. великий русский математик Николай Иванович Лобачевский, который создал новую, неевклидову геометрию, называемую ныне геометрией Лобачевского.
Слайд 8
Открытие Лобачевского было началом нового периода
в развитии геометрии. За ним последовали новые открытия немецкого
математика Б. Римана и др. В настоящее время геометрия тесно переплетается со многими другими разделами математики. Одним из источников развития и образования новых понятий в геометрии, как и в других областях математики, являются современные задачи естествознания, физики и техники.
Лобачевский
Слайд 9
О развитии геометрии в Древней Греции
до Евклида
Ученые и философы Древней Греции восприняли и переработали достижения культуры и науки Древнего Востока. Фалес, Пифагор, Демокрит, Евдокс и др. ездили в Египет и Вавилон для изучения музыки, математики и астрономии. Не случайно зачатки греческой геометрической науки связаны с именем Фалеса Милетского, основателя ионийской школы. Ионийцы, населявшие территорию, которая граничила с восточными странами, первыми заимствовали знания Востока и стали их развивать.
Слайд 10
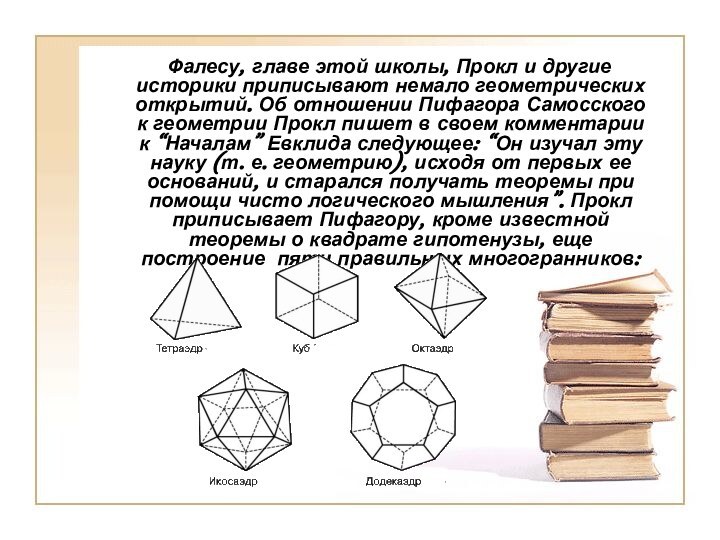
Фалесу, главе этой школы, Прокл и
другие историки приписывают немало геометрических открытий. Об отношении Пифагора
Самосского к геометрии Прокл пишет в своем комментарии к “Началам” Евклида следующее: “Он изучал эту науку (т. е. геометрию), исходя от первых ее оснований, и старался получать теоремы при помощи чисто логического мышления”. Прокл приписывает Пифагору, кроме известной теоремы о квадрате гипотенузы, еще построение пяти правильных многогранников:
Слайд 11
Грани додекаэдра являются правильными пятиугольниками.
Диагонали же правильного пятиугольника образуют так называемый звездчатый пятиугольник
- фигуру, которая служила эмблемой, опознавательным знаком для учеников Пифагора. Известно, что пифагорейский союз был одновременно философской школой, политической партией и религиозным братством. Согласно легенде, один пифагореец заболел на чужбине и не мог перед смертью расплатиться с ухаживавшим за ним хозяином дома. Последний нарисовал на стене своего дома звездчатый пятиугольник. Увидав через несколько лет этот знак, другой странствующий пифагореец осведомился о случившемся у хозяина и щедро его вознаградил.
Слайд 12
Многогранники
Поверхность, составленную из многоугольников и ограничивающую некоторое
геометрическое тело, называется многогранником.(представители)
параллелограмм
Слайд 13
Призма
Рассмотрим два равных многоугольника A1A2…
An и B1B2… Bn, расположенных в параллельных плоскостях а
и b так, что отрезки A1B1, A1B2…, AnBn, соединяющие соответственные вершины многоугольников, параллельны. Каждый из n четырехугольников
A1A2B2B1,A2A3B3B2, …,AnA1B1Bn
является параллелограммом, так как имеет попарно параллельные противоположные стороны. Например, в четырехугольнике A1A2B2B1 стороны
Слайд 14
A1B1 и A2B2 параллельны
по условию, а стороны A1A2 и B1B2 – по
свойству параллельных плоскостей, пересеченных третьей плоскостью.
Многогранник, составленный из двух равных многоугольников A1A2…An и B1B2…Bn, расположенных в параллельных плоскостях, и n параллелограммов, называется призмой.
Если боковое ребро призмы перпендикулярно плоскости ее основания, то такую призму называют прямой; если боковое ребро призмы не перпендикулярно плоскости ее основания, то такую призму называют наклонной. У прямой призмы боковые грани - прямоугольники. Перпендикуляр к плоскостям оснований, концы которого принадлежат этим плоскостям, называют высотой призмы.
Прямая призма, основанием которой служит правильный многоугольник, называется правильной призмой.
Слайд 15
Площадь поверхности призмы
Поверхность многогранника состоит из конечного
числа многоугольников (граней). Площадь поверхности многогранника есть сумма площадей
всех его граней. Площадь поверхности призм (Sпр) равна сумме площадей ее боковых
граней (площади боковой поверхности Sбок) и площадей двух оснований (2Sосн) - равных многоугольников: Sпр=Sбок+2Sосн.
пирамида
Подобно тому, как треугольник в понимании Евклида не
являются пустым, т. е. представляет собой часть плоскости, ограниченную тремя неконкурентными (т. е. не пересекающимися в одной точке) отрезками, так и многогранник у него не пустой, не полый, а чем-то заполненный (по-нашему - частью пространства). В античной математике, однако, понятия отвлеченного пространства еще не было. Евклид определяет призму как телесную фигуру, заключенную между двумя
Слайд 17
равными и параллельными плоскостями (основаниями) и с боковыми
гранями - параллелограммами. Для того чтобы это определение было
вполне корректным, следовало бы, однако, доказать, что плоскости, проходящие через пары непараллельных сторон оснований, пересекаются по параллельным прямым. Евклид употребляет термин “плоскость” как в широком смысле (рассматривая ее неограниченно продолженной во все направления), так и в смысле конечной, ограниченной ее части, в частности грани, аналогично применению им термина “прямая” (в широком смысле - бесконечная прямая и в узком - отрезок). В XVIII в. Тейлор дал такое определение призмы: это многогранник, у которого все грани, кроме двух, параллельны одной прямой.
Слайд 18
Пирамиду Евклид определяет
как телесную фигуру, ограниченную плоскостями, которые от одной плоскости
(основания) сходятся в одной точке
(вершине). Эго определение подвергалось критике уже в древности, например, Героном, предложившим следующее определение пирамиды: это фигура, ограниченная треугольниками, сходящимися в одной точке, и основанием которой служит многоугольник.
Слайд 19
Важнейшим недостатком этого определения является использование неопределенного понятия
основания. Тейлор определил пирамиду как многогранник, у которого все
грани, кроме одной, сходятся в одной точке. Лежандр в “Элементах геометрии” так определяет пирамиду: “Телесная фигура, образованная треугольниками, сходящимися в одной точке и заканчивающаяся на различных сторонах плоского основания”. После этой формулировки разъясняется понятие основания. Определение Лежандра является явно избыточным, т.е. содержит признаки, которые можно вывести из других. А вот еще одно определение, которое фигурировало в учебниках ХIХ в.: пирамида - телесный угол, пересеченный плоскостью.
Слайд 20
Еще в древности существовали два пути определения геометрических
понятий. Первый вел от фигур высшего порядка к фигурам
низшего. Такой точки зрения придерживался, в частности, Евклид, определяющий поверхность как границу тела, линию - как границу поверхности, концы же линии - как точки. Второй путь ведет, наоборот, от фигур низшего измерения к фигурам высшего: движением точки образуется линия, аналогично из линий составляется поверхность и т. д. Одним из первых, который соединил обе эти точки зрения, был Герон Александрийский, писавший, что тело ограничивается поверхностью и вместе с этим может быть рассмотрено как образованное движением поверхности.
В появившихся позже на протяжении веков учебниках геометрии принималась за основу то
одна, то другая, а иногда и обе вместе точки зрения.
Слайд 21
Многогранник, одна из граней которого -
многоугольник, а остальные грани - треугольники с общей вершиной,
называется пирамидой. Пирамида, основание которой - правильный многоугольник и вершина проектируется в его центр, называется правильной.
объемов
Объемы зерновых амбаров и других сооружений в виде
кубов, призм и цилиндров египтяне и вавилоняне, китайцы и индийцы вычисляли путем умножения площади основания на высоту. Однако древнему Востоку были известны в основном только отдельные правила, найденные опытным путем, которыми пользовались для нахождения объемов для площадей фигур. В более позднее время, когда геометрия сформировалась как наука, был найден общий подход к вычислению объемов многогранников.
Слайд 23
Среди замечательных греческих ученых V - IV вв.
до н.э., которые разрабатывали теорию объемов, были Демокрит из
Абдеры и Евдокс Книдский.
Евклид не применяет термина “объем”. Для него термин “куб”, например, означает и объем куба. В ХI книге “Начал” изложены среди других и теоремы следующего содержания.
Параллелепипеды с одинаковыми высотами и равновеликими основаниями равновелики.
Отношение объемов двух параллелепипедов с равными высотами равно отношению площадей их оснований.
3. В равновеликих параллелепипедах площади оснований обратно пропорциональны высотам
Теоремы Евклида относятся только к сравнению объемов, так как непосредственное вычисление объемов тел Евклид, вероятно, считал делом практических руководств по геометрии. В произведениях прикладного характера Герона Александрийского имеются правила для вычислений объема куба, призмы, параллелепипеда и других пространственных фигур.
Евдокс
объеме
Термин “пирамида” заимствован из греческого “пирамис”
или “пирамидос”. Греки в свою очередь позаимствовали это слово, как полагают, из египетского языка. В папирусе Ахмеса встречается слово “пирамус” в смысле ребра правильной пирамиды. Другие считают, что термин берет свое начало от форм хлебцев в Древней Греции “пирос” - рожь). В связи с тем, что форма пламени иногда напоминает образ пирамиды, некоторые средневековые ученые считали, что термин происходит греческого слова “пир” - огонь. Вот почему в некоторых учебниках геометрии XVI в. пирамида названа “огнеформное тело”.
Слайд 25
Согласно Архимеду, еще в V до н.э. Демокрит
из Абдеры установил, что объем пирамиды равен одной трети
объема призмы с тем же основанием и той же высотой. Полное доказательство этой теоремы дал Евдокс Книдский в IV до н.э.
Египетские пирамиды
(по середине пирамида Хеопса высота которой достигает 147м)
Слайд 26
О призме и параллелепипеде
Часть геометрии, в которой

изучаются свойства куба, призмы, параллелепипеда и других геометрических тел
и пространственных фигур, издавна называется стереометрией; Слово это греческого происхождения (“стереос” - пространственный, “метрео” - измеряю) и встречается еще у знаменитого древнегреческого философа Аристотеля. Стереометрия возникла позже, чем планиметрия. Евклид дает следующее определение призмы: “Призма есть телесная (т.е. пространственная) фигура, заключенная между плоскостями, из которых две противоположные равны и параллельны, остальные же - параллелограммы”. Тут, как и во многих других местах, Евклид употребляет термин “плоскость” не в смысле безгранично продолженной плоскости, а в смысле ограниченной ее части, грани, подобно тому как “прямая” означает у него и отрезок прямой.
Термин “призма” греческого происхождения и буквально означает “отпиленное” (тело).
Термин “параллелепипедальное тело” встречается впервые у Евклида и означает дословно “параллеле-плоскостное тело”. Греческое слово “кубос” употребляется Евклидом в том же смысле, что и наше слово “куб”.
Параллелепипед
Призма, основание которой - параллелограмм, называется параллелепипедом.
В соответствии
с определением параллелепипед - это четырехугольная призма, все грани которой - параллелограммы. Параллелепипеды, как и призмы, могут быть прямыми и наклонными.
Прямой параллелепипед, основанием которого служит прямоугольник, называют прямоугольным параллелепипедом. У прямоугольного параллелепипеда все грани прямоугольники.