- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Определение параболы
Содержание
- 2. Определение параболыПусть на плоскости задана прямая d
- 3. Упражнение 2Нарисуйте ГМТ A’, для которых расстояние до фокуса меньше расстояния до директрисы.
- 4. Упражнение 3Нарисуйте ГМТ A”, для которых расстояние до фокуса больше расстояния до директрисы.
- 5. Рисуем параболуПараболу можно нарисовать с помощью линейки, угольника, кнопок, нитки и карандаша.
- 6. Касательная к параболеПрямая, имеющая с параболой только
- 7. Фокальное свойство параболыЕсли источник света поместить в
- 8. Построение касательнойПо данному рисунку укажите способ построения
- 9. Упражнение 4Сколько касательных можно провести к параболе
- 10. Упражнение 5Что будет происходить с параболой, если фокус: а) удаляется от директрисы; б) приближается к директрисе?
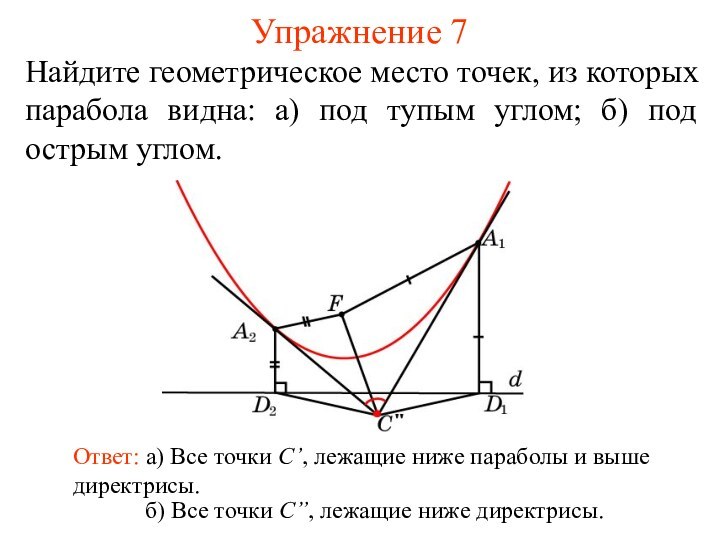
- 11. Упражнение 6Найдите геометрическое место точек, из которых парабола видна под прямым углом.
- 12. Скачать презентацию
- 13. Похожие презентации
Определение параболыПусть на плоскости задана прямая d и точка F, не принадлежащая этой прямой. Геометрическое место точек, равноудаленных от прямой d и точки F, называется параболой. Прямая d называется директрисой, а точка F - фокусом параболы.
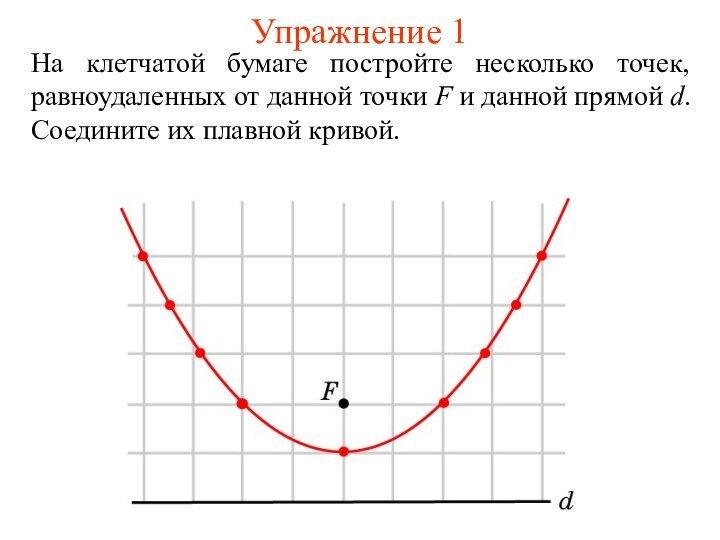









Слайд 3
Упражнение 2
Нарисуйте ГМТ A’, для которых расстояние до
фокуса меньше расстояния до директрисы.
Слайд 4
Упражнение 3
Нарисуйте ГМТ A”, для которых расстояние до
фокуса больше расстояния до директрисы.
Слайд 5
Рисуем параболу
Параболу можно нарисовать с помощью линейки, угольника,
кнопок, нитки и карандаша.
Слайд 6
Касательная к параболе
Прямая, имеющая с параболой только одну
общую точку и не перпендикулярная ее директрисе, называется касательной
к параболе. Общая точка называется точкой касания.
Слайд 7
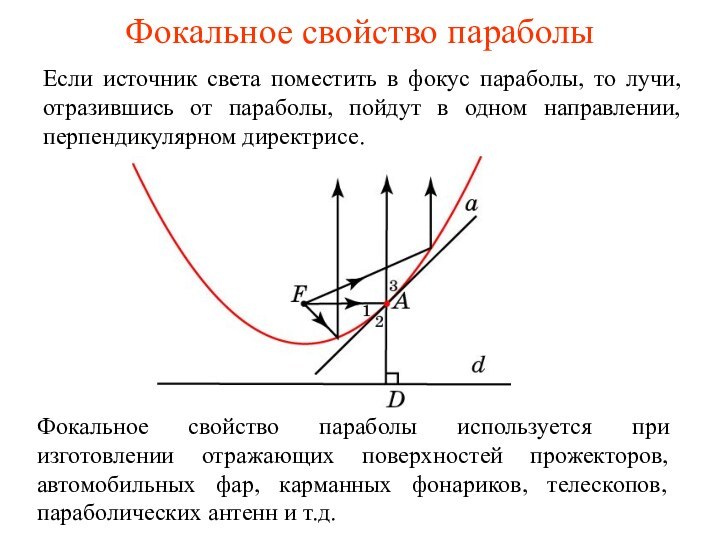
Фокальное свойство параболы
Если источник света поместить в фокус
параболы, то лучи, отразившись от параболы, пойдут в одном
направлении, перпендикулярном директрисе.Фокальное свойство параболы используется при изготовлении отражающих поверхностей прожекторов, автомобильных фар, карманных фонариков, телескопов, параболических антенн и т.д.
Слайд 8
Построение касательной
По данному рисунку укажите способ построения касательной
к параболе, заданной фокусом F и директрисой d, проходящей
через точку C, с помощью циркуля и линейки.
Слайд 9
Упражнение 4
Сколько касательных можно провести к параболе из
точки: а) принадлежащей параболе; б) лежащей ниже параболы; в)
лежащей выше параболы?Ответ: а) Одну;
б) две;
в) ни одной.