- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Правильные выпуклые многогранники
Содержание
- 2. Правильные выпуклые многогранники
- 3. Проблема исследованияОпределение правильного многогранникаВиды правильных многогранниковЭлементы симметрии и формулыНемного историиИспользованные материалыСодержание
- 4. Правильных многогранников вызывающе мало, но этот весьма
- 5. Проблема исследования Изучение многогранников
- 6. Определение: Выпуклый многогранник называется правильным,
- 7. Виды правильных многогранниковтетраэдргексаэдроктаэдрдодекаэдрикосаэдр К содержанию
- 8. Составлен из восьми равносторонних треугольников. Каждая вершина
- 9. Составлен из шести квадратов. Каждая
- 10. Правильный тетраэдр Составлен из четырёх равносторонних
- 11. Правильный додекаэдр Составлен из двенадцати
- 12. Правильный икосаэдрСоставлен из двадцати равносторонних треугольников. Каждая
- 13. Элементы симметрии и формулы:ОктаэдрТетраэдрГексаэдр (куб)ДодекаэдрИкосаэдр
- 16. Гексаэдр (куб)Куб
- 17. Додекаэдр Додекаэдр имеет центр симметрии - центр
- 19. Таблица № 1
- 20. Таблица № 2
- 21. Свойства этих многогранников изу-чали ученые и священники;
- 22. Великий древнегреческий ученый Платон, живший в IV-V
- 23. Но оставался еще додекаэдр - отсутствует полное
- 24. Использовались материалы:http://www.vschool.ruhttp://center.fio.ruhttp://gemsnet.ruhttp://alzl.narod.ruПрограммы:Microsoft WordMicrosoft Power PointInternet Explorer
- 25. Скачать презентацию
- 26. Похожие презентации

























Слайд 3
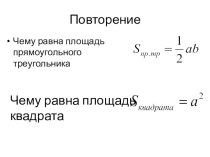
Проблема исследования
Определение правильного многогранника
Виды правильных многогранников
Элементы симметрии и
формулы
Слайд 4 Правильных многогранников вызывающе мало, но этот весьма скромный
по численности отряд сумел пробраться в самые глубины различных
наук.Л.Кэрролл
Слайд 5
Проблема исследования
Изучение многогранников на
протяжении всей истории велось не только с позиций дальнейшего
их применения, но и с целью осмысления философских вопросов об устройстве Вселенной и природе Пространства
Слайд 6
Определение:
Выпуклый многогранник называется правильным, если все
его грани равные правильные многоугольники и, кроме того, в
каждой вершине сходится одинаковое число ребер.Существует всего 5 видов правильных многогранников
Слайд 8 Составлен из восьми равносторонних треугольников. Каждая вершина октаэдра
является вершиной четырёх треугольников. Следовательно, сумма плоских углов
при каждой вершине 240º.Правильный октаэдр
Рис. 1
Слайд 9 Составлен из шести квадратов. Каждая вершина
куба является вершиной трёх квадратов. Следовательно, сумма плоских углов
при каждой вершине равна 270º. Куб (гексаэдр)
Рис. 3
Слайд 10
Правильный тетраэдр
Составлен из четырёх равносторонних треугольников.
Каждая его вершина является вершиной трёх треугольников. Следовательно, сумма
плоских углов при каждой вершине равна 180º.Рис. 2
Слайд 11
Правильный додекаэдр
Составлен из двенадцати правильных
пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников.
Следовательно, сумма плоских углов при каждой вершине равна 324º.Рис. 4
Слайд 12
Правильный икосаэдр
Составлен из двадцати равносторонних треугольников. Каждая вершина
икосаэдра является вершиной пяти треугольников. Следовательно, сумма плоских углов
при каждой вершине равна 300º.Рис. 5
Слайд 14
Октаэдр
Октаэдр имеет центр симметрии -
центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии.Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности:
Объем октаэдра:
к содержанию
Слайд 15
Тетраэдр
Тетраэдр не имеет центра симметрии, но имеет
3 оси симметрии и 6 плоскостей симметрииРадиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности:
Объем тетраэдра:
к содержанию
Слайд 16
Гексаэдр (куб)
Куб имеет
центр симметрии - центр куба, 9 осей
симметрии и
9 плоскостей симметрии.
Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности куба:
Объем куба:
К содержанию
Слайд 17
Додекаэдр
Додекаэдр имеет центр симметрии - центр додекаэдра,
15 осей симметрии и 15 плоскостей симметрии.
Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности:
Объем додекаэдра:
К содержанию
Слайд 18
Икосаэдр
Икосаэдр имеет центр симметрии - центр икосаэдра, 15
осей симметрии и 15 плоскостей симметрии.Радиус описанной сферы:
Радиус вписанной сферы:
Площадь поверхности:
Объем икосаэдра:
К содержанию
Слайд 21
Свойства этих многогранников изу-
чали ученые и священники; их
мо-
дели можно увидеть в работах ар-
хитекторов и ювелиров,
им припи-сывались различные магические и
целебные свойства.
Немного истории
К содержанию
Слайд 22 Великий древнегреческий ученый Платон, живший в IV-V вв.
до н. э., считал, что эти тела олицетворяют сущность
природы. Человечеству были известны четыре сущности: огонь, вода, земля и воздух. По мнению Платона, их атомы имели вид правильных многогранников: огня — тетраэдр, земли — гексаэдр, воздуха - октаэдр, воды — икосаэдр.к содержанию
Слайд 23 Но оставался еще додекаэдр - отсутствует полное соответствие.
Платон предположил, что существует еще одна сущность - мировой
эфир, атомы которого имеют вид додекаэдра. Платон и его ученики в своих работах уделяли большое внимание правильным многогранникам, и поэтому их ещё называют "платоновыми телами".К содержанию