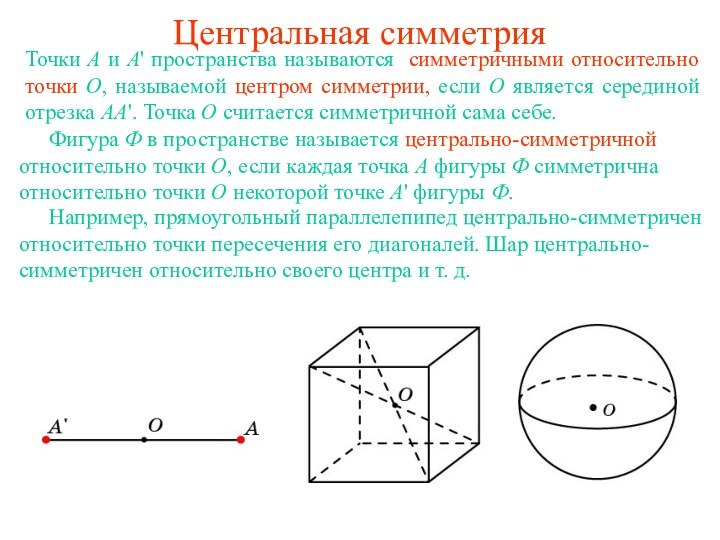
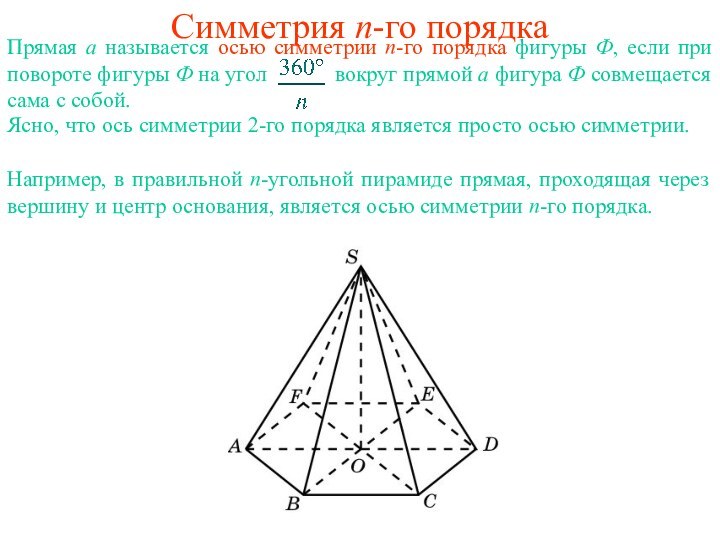
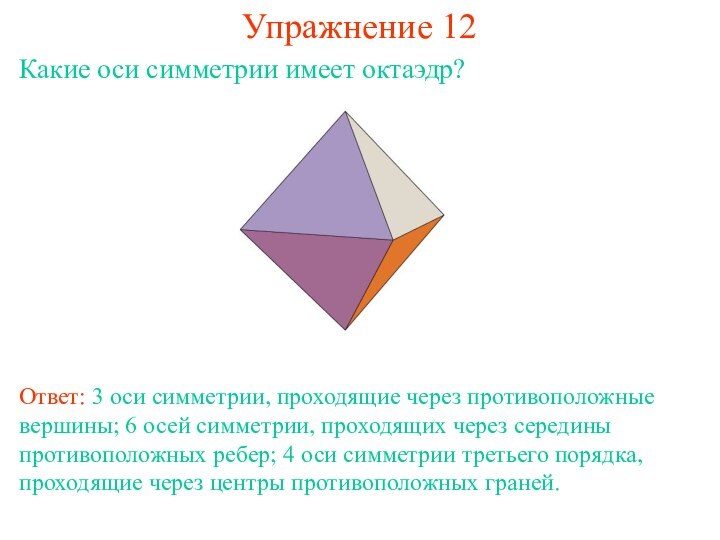
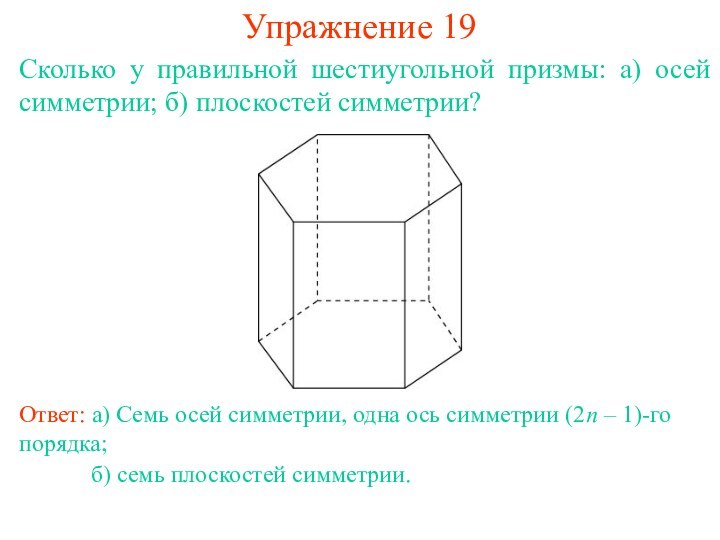
относительно прямой a, называемой осью симметрии, если прямая a
проходит через середину отрезка AA' и перпендикулярна этому отрезку. Точки прямой a считаются симметричными сами себе. Фигура Ф в пространстве называется симметричной относительно оси a, если каждая точка A фигуры Ф симметрична относительно этой оси некоторой точке A' фигуры Ф.
Например, прямоугольный параллелепипед симметричен относительно оси, проходящей через центры противоположных граней, прямой круговой цилиндр симметричен относительно своей оси и т. д.