- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии на тему Понятие площади
Содержание
- 2. Знание – это самое превосходное из владений. Все стремятся к нему, само оно не приходит.Абу-р-Райхан ал-Буруни
- 3. Как найти площадь комнаты, где вы живёте
- 4. Если требуется найти полную площадь квартиры?
- 5. 21. 10. 16Классная работаПонятие площади. Измерение площади.
- 6. Фигура?Число ?Что-то другое ?
- 7. Определение Для многоугольных фигур площадью называется положительная
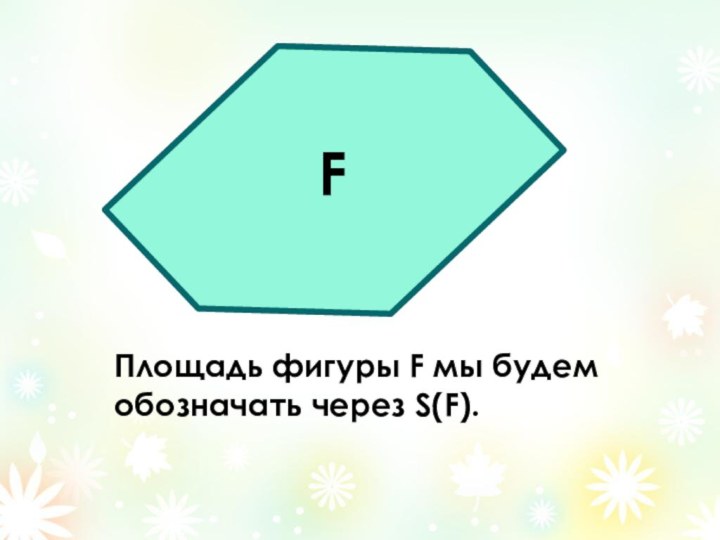
- 8. Площадь фигуры F мы будем обозначать через S(F).F
- 9. F1F2F3F4F5F6S = S(F1) + S(F2) + S(F3) + S(F4) + S(F5) + S(F6)
- 11. Площадь поверхности многогранника – это сумма площадей его граней.
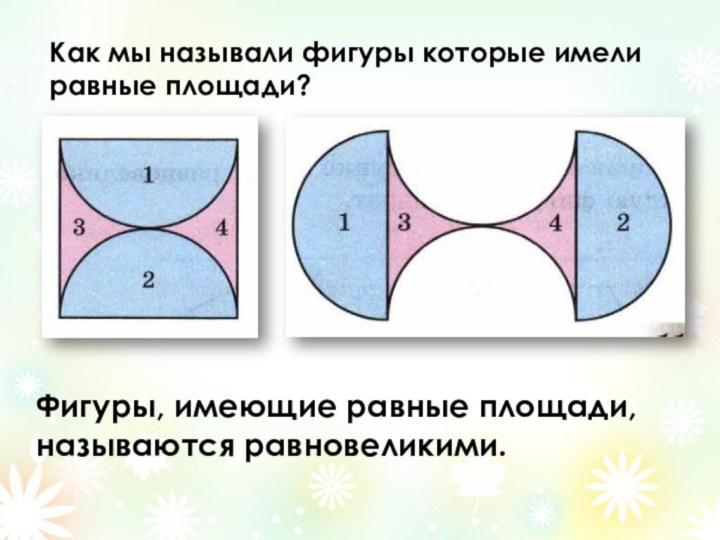
- 12. Фигуры, имеющие равные площади, называются равновеликими.Как мы называли фигуры которые имели равные площади?
- 13. Простейший пример равновеликих фигур дают равные треугольники:
- 14. Измерение площади состоит
- 15. За единицу измерения площади принимают площадь квадрата,
- 16. Дополняем теорию.Стр.37 № 2.1
- 17. Скачать презентацию
- 18. Похожие презентации
Знание – это самое превосходное из владений. Все стремятся к нему, само оно не приходит.Абу-р-Райхан ал-Буруни















Слайд 3 Как найти площадь комнаты, где вы живёте ?
Как найти жилую площадь квартиры,
в которой несколько комнат?
Слайд 7
Определение
Для многоугольных фигур площадью называется положительная величина
с такими свойствами :
1) площадь фигуры, составленной из
нескольких фигур, равна сумме
площадей этих фигур;
2) равные треугольники имеют одну и ту
же площадь.
Слайд 12
Фигуры, имеющие равные площади, называются равновеликими.
Как мы называли
фигуры которые имели
равные площади?
Слайд 13 Простейший пример равновеликих фигур дают равные треугольники: они
равновелики по свойству 2. Используя свойство 1, получаем более
общее утверждение: если фигуры составлены из попарноравных треугольников, то они равновелики (рис. 58). В частности, равные квадраты (квадраты с равными сторонами) равновелики.
Действительно, диагонали разбивают их на равные прямоугольные
треугольники (рис. 59).
Слайд 14 Измерение площади состоит
в сравнении площади
даннойфигуры с площадью фигуры, принятой за единицу измерения. В результате получится численное значение площади данной фигуры.
Слайд 15 За единицу измерения площади принимают площадь квадрата, стороной
которого является некоторая единица длины.
Например, жилую площадь измеряют
в квадратных метрах, площадь государства - в квадратных километрах. Тогда пишут, например, 20 м² или 156 ООО км². Когда наименование единицы длины не указано, о численном значении площади фигуры F пишем, например, так: S(F) = 15 кв. ед. Запись S(F) = 15 является сокращением записи S(F) = 15 кв. ед.





























