- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Электронное пособие Уроки стереометрии
Содержание
- 2. Взаимное расположение точек, прямых и плоскостей в простанстве
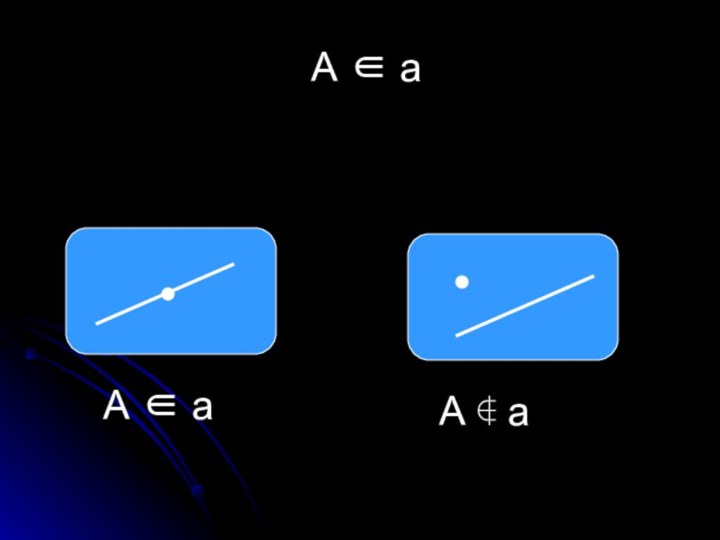
- 3. А ∈ aА ∈ aА ∉ a
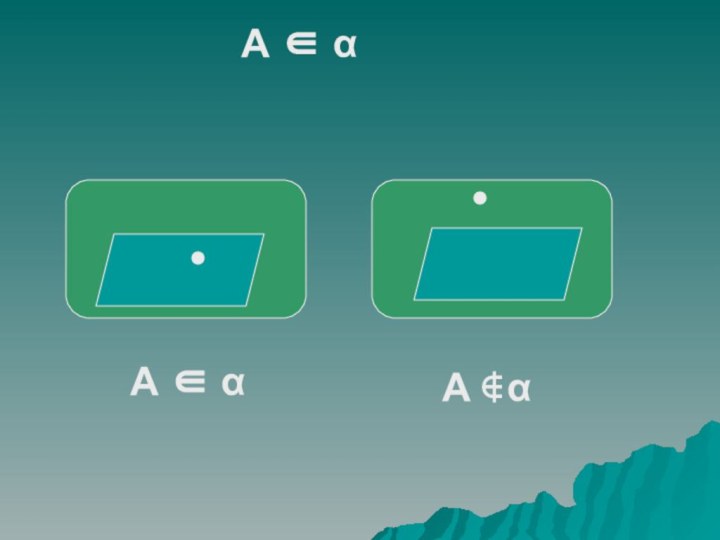
- 4. А ∈ α А ∈ α А ∉ α
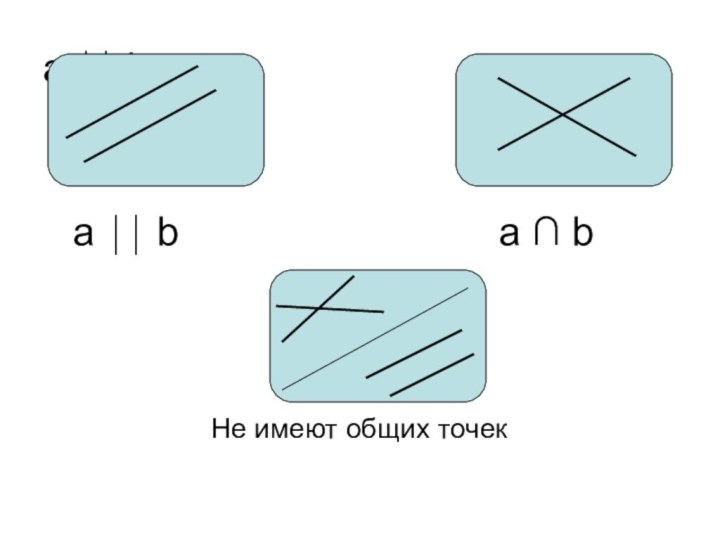
- 5. a ⏐⏐ ba ⏐⏐ ba ∩ bНе имеют общих точек
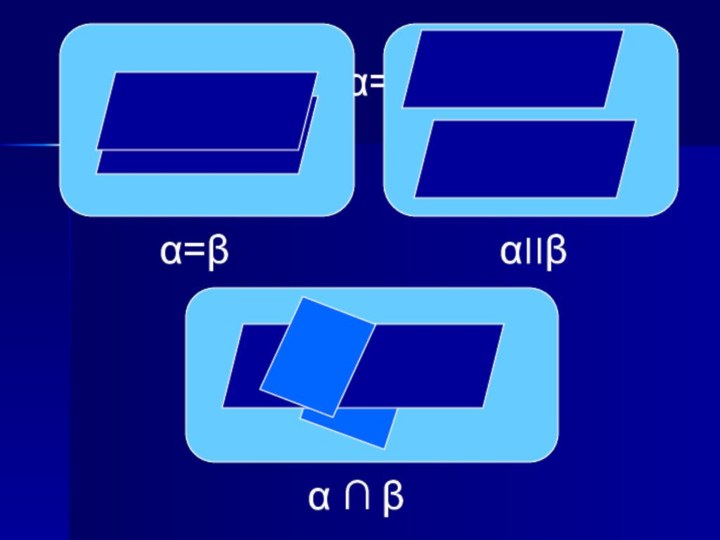
- 6. α=βα=βα׀׀βα ∩ β
- 7. a ⊂ αa ⊂ αa ∩ α a ׀׀ α
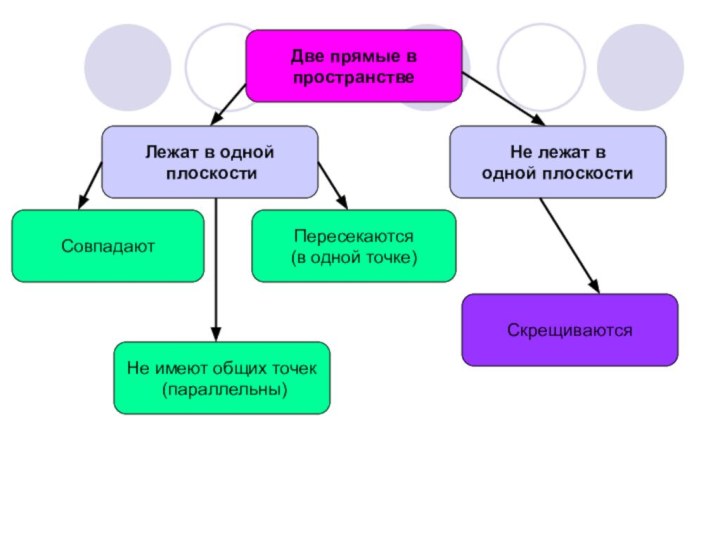
- 8. Взаимное расположение двух прямых в пространстве
- 9. Две прямые в пространствеДве прямые в пространствеЛежат
- 10. Имеют единственную общую точкуИмеют единственную общую точкуИмеют
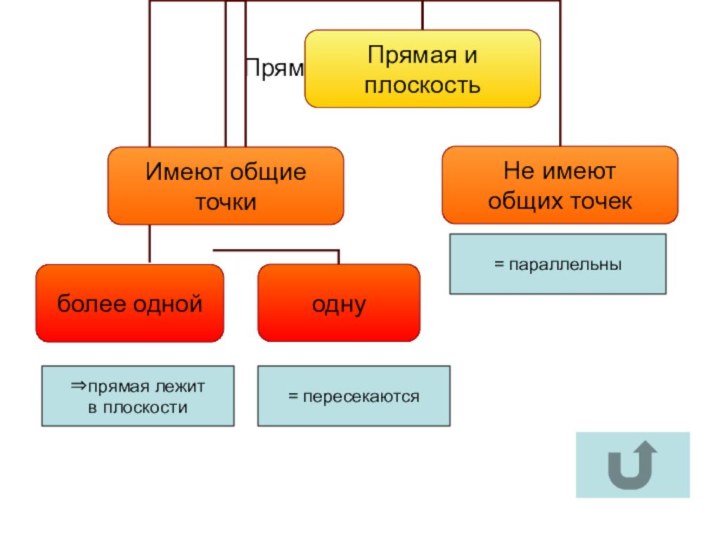
- 11. Параллельность прямой и плоскости
- 12. Прямая и плоскость⇒прямая лежит в плоскости= пересекаются= параллельны
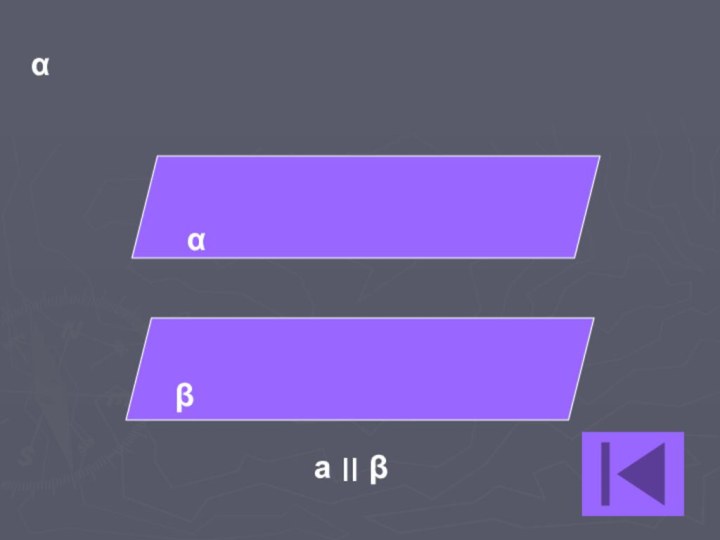
- 13. Параллельные плоскости
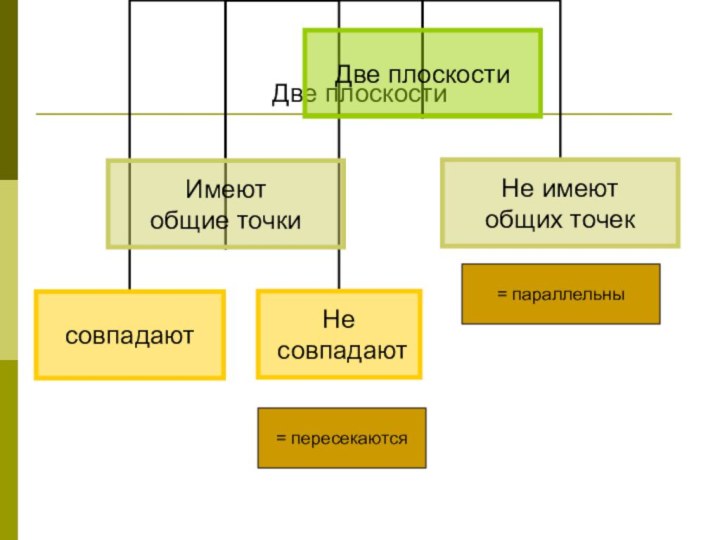
- 14. Две плоскости= пересекаются= параллельны
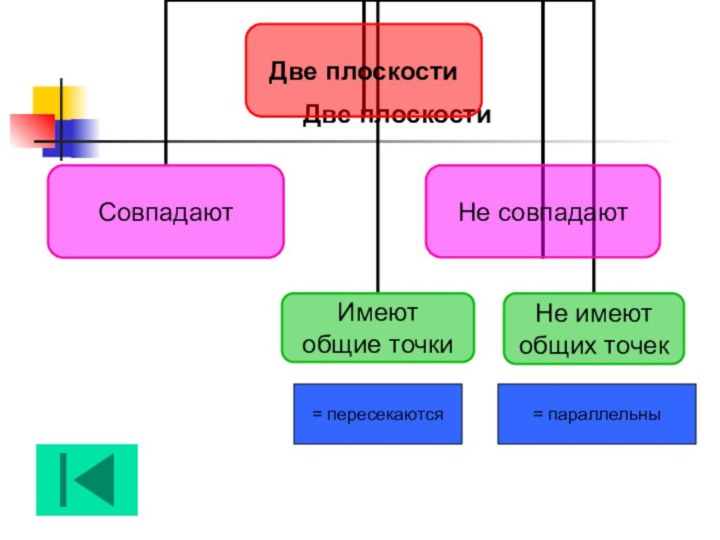
- 15. Две плоскости= пересекаются= параллельны
- 16. Основные аксиомы и определения
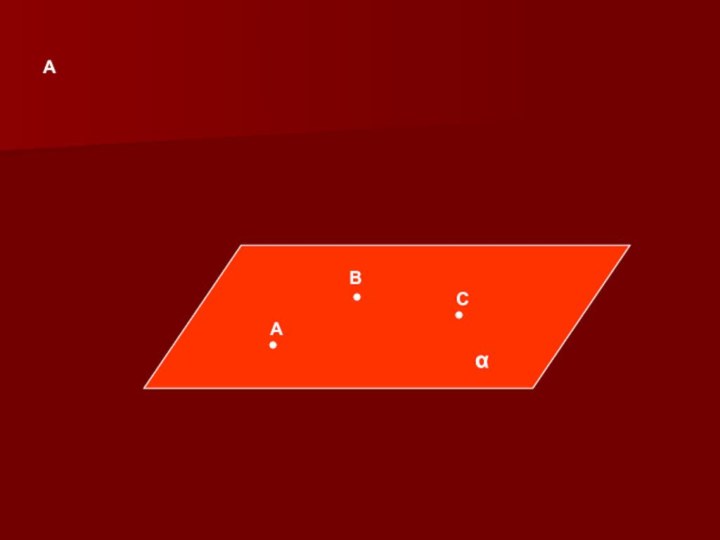
- 17. Через любые три точки, не лежащие на одной прямой, проходит одна и только одна плоскость
- 18. ААВСα
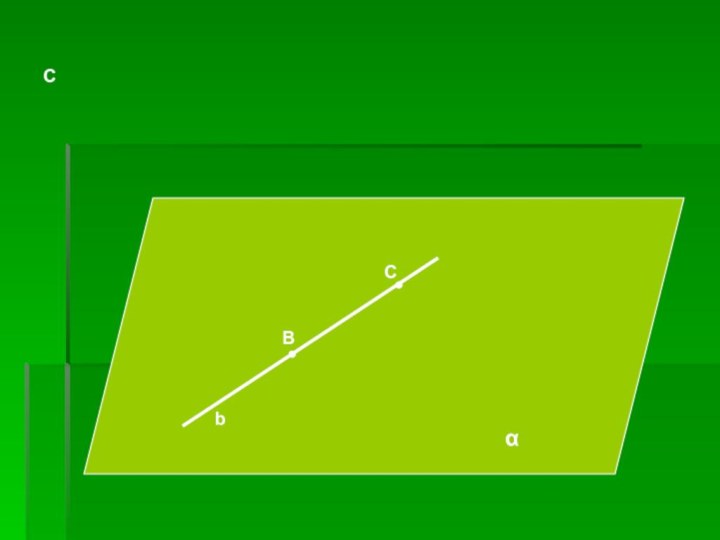
- 19. Если две точки прямой лежат в плоскости, то и вся прямая лежит в этой плоскости.
- 20. ССαВb
- 21. Прямая называется параллельной плоскости, а плоскость – параллельной прямой, если они не имеют общих точек.
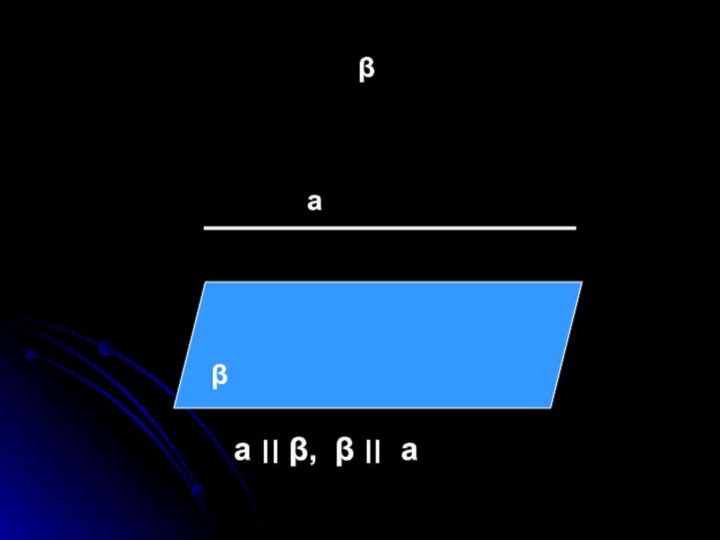
- 22. ββа а ׀׀ β, β ׀׀ а
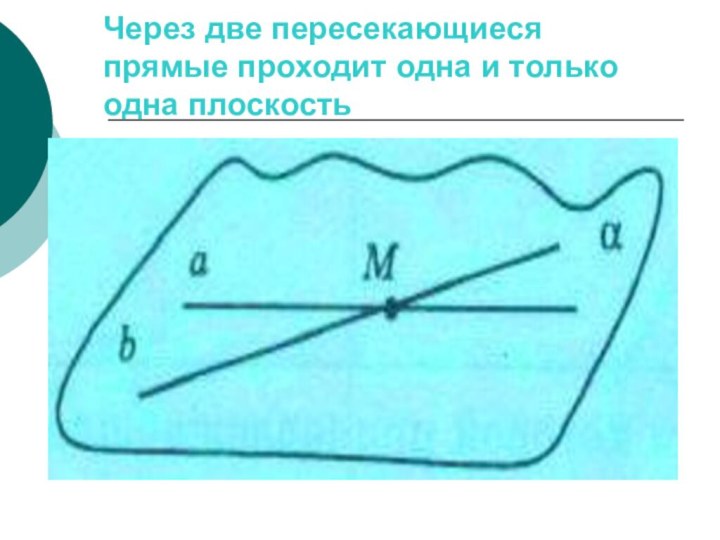
- 23. Две прямые, имеющие только одну общую точку, называются пересекающимися
- 24. МММаbа ∩ b = М
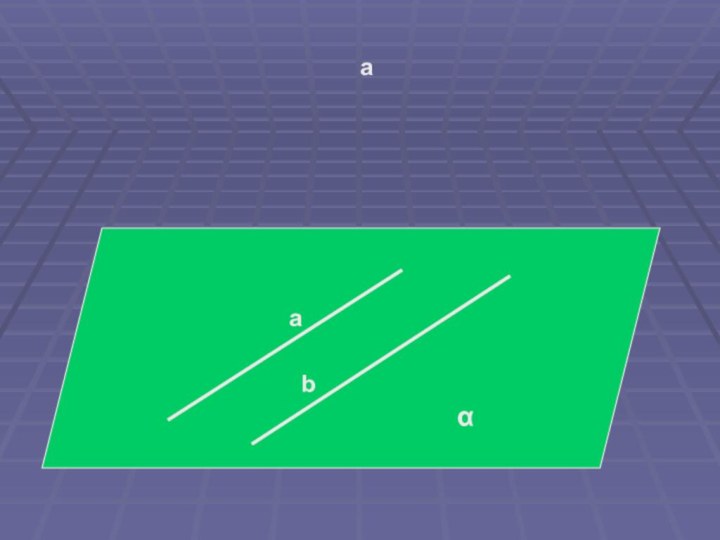
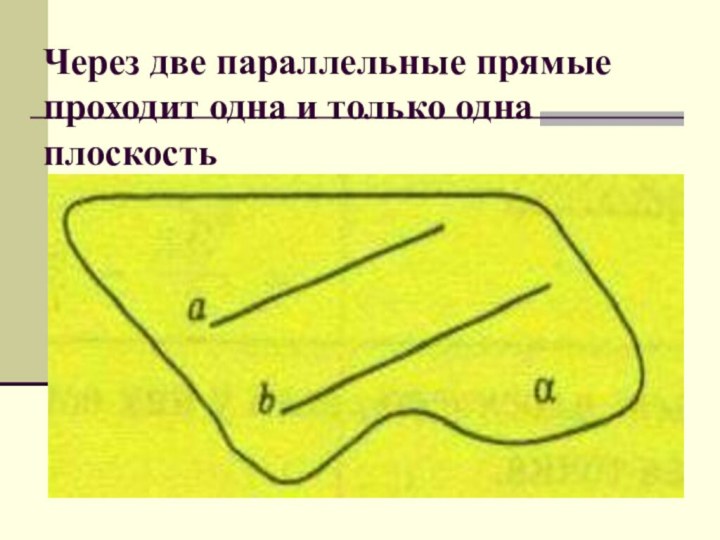
- 25. Две прямые, лежащие в одной плоскости и не имеющие общих точек, называются параллельными.
- 26. ааbα
- 27. Прямая, все точки которой принадлежат плоскости, называется прямой, лежащей в этой плоскости.
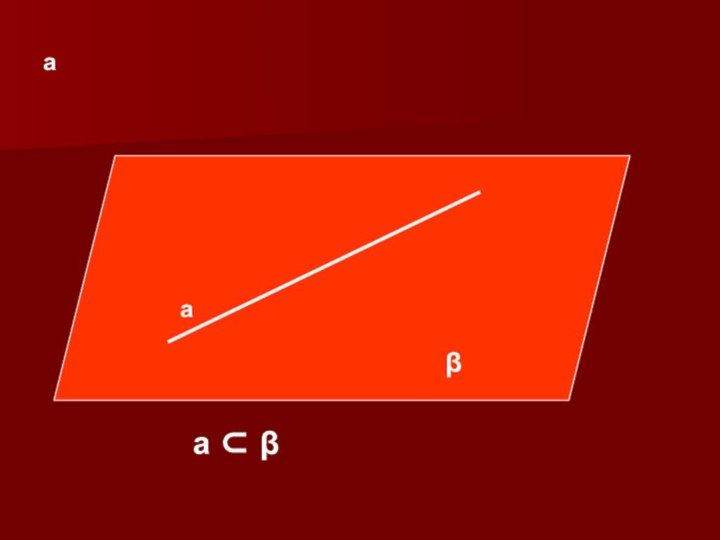
- 28. ааβа ⊂ β
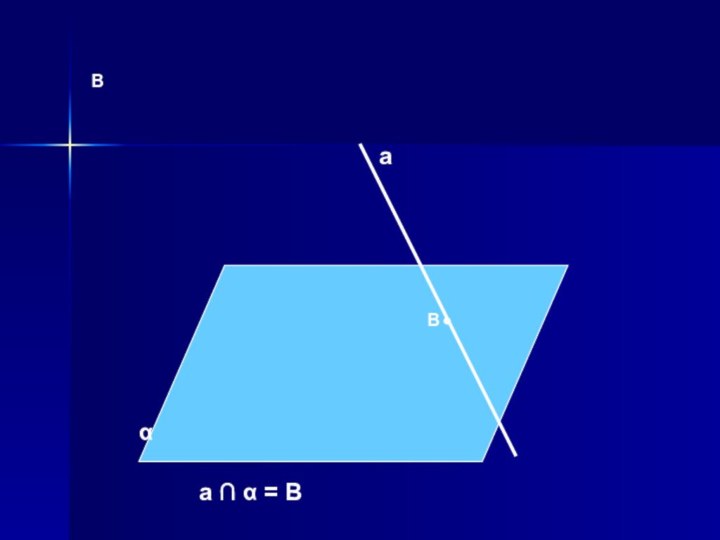
- 29. Прямая пересекает плоскость, если у них есть только одна общая точка.
- 30. ВВαаа ∩ α = В
- 31. Две плоскости, не имеющие общих точек, называются параллельными
- 32. ααβа ׀׀ β
- 33. Прямая называется перпендикулярной плоскости (а плоскость прямой), если прямая перпендикулярна любой прямой лежащей в этой плоскости.
- 34. ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИЕсли прямая перпендикулярна
- 36. СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИЕсли плоскость перпендикулярна
- 37. ααab
- 38. ПЕРПЕНДИКУЛЯР И НАКЛОННАЯПерпендикуляром, опущенным из данной точки
- 39. Наклонной, проведенной из данной точки к данной
- 40. ααВСА
- 41. Двугранным углом называется фигура, образованная двумя полуплоскостями
- 43. Линейным углом двугранного угла называется пересечение этого двугранного угла и плоскости перпендикулярной его ребру.
- 44. Трехгранным углом (аbс) называется фигура, составленная из
- 46. Две пересекающиеся плоскости называются перпендикулярными, если
- 47. ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙЕсли плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
- 49. Теоремы стереометрии
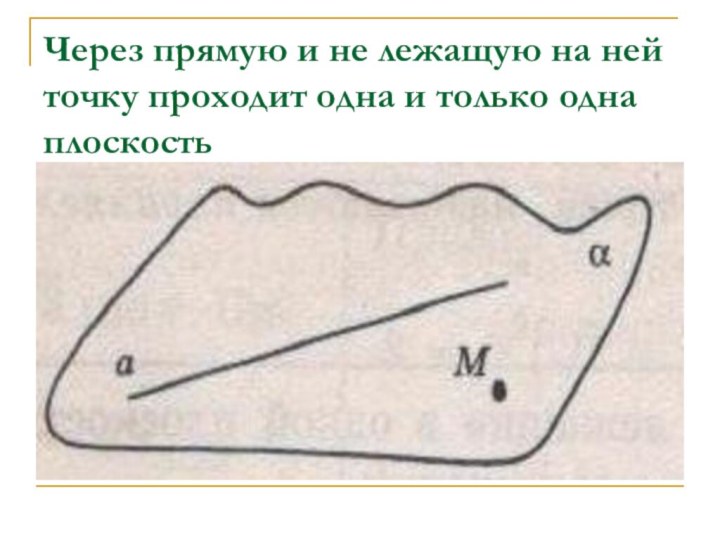
- 50. Через прямую и не лежащую на ней точку проходит одна и только одна плоскость
- 51. Через две пересекающиеся прямые проходит одна и только одна плоскость
- 52. Через две параллельные прямые проходит одна и только одна плоскость
- 53. Если точки A, B, C, D не
- 54. Если одна из параллельных прямых пересекает плоскость,
- 55. Признак параллельности прямыхЕсли две прямые параллельны третьей, то они параллельны между собой
- 56. Признак параллельности прямой и плоскости
- 57. Если одна из пересекающихся плоскостей проходит через
- 58. Если каждая из пересекающихся плоскостей проходит через
- 59. Если две пересекающиеся плоскости пересечены третьей плоскостью
- 60. Если две пересекающиеся плоскости пересечены третьей плоскостью
- 61. Признаки параллелельности плоскостей
- 62. Если две пересекающиеся прямые одной плоскости
- 63. Если две плоскости параллельны третьей, то они
- 64. Свойства параллельных плоскостей
- 65. Если плоскость пересекает две параллельные плоскости, то
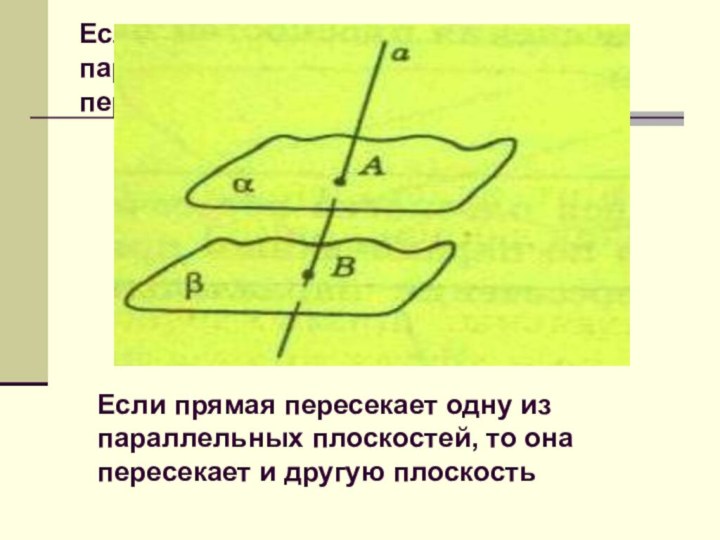
- 66. Если прямая пересекает одну из параллельных плоскостей,
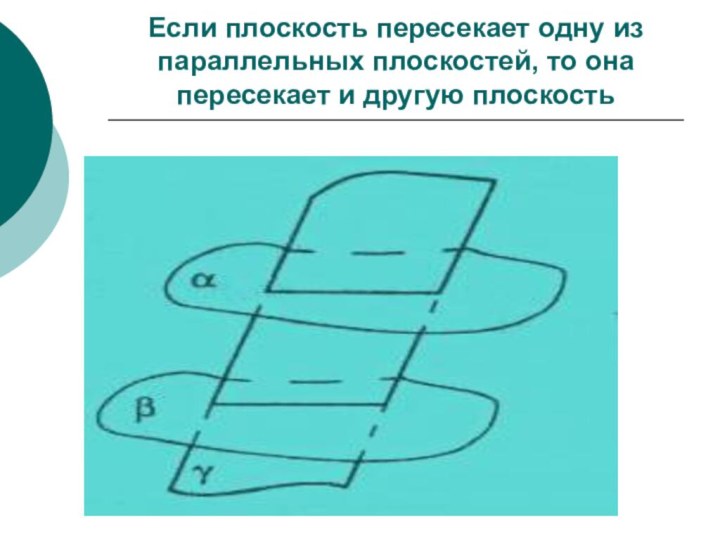
- 67. Если плоскость пересекает одну из параллельных плоскостей, то она пересекает и другую плоскость
- 68. Через точку, не лежащую на плоскости, можно
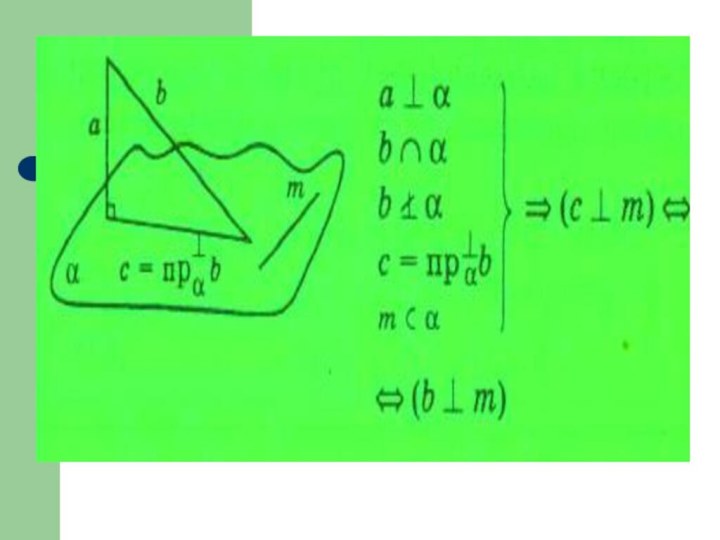
- 69. Если (ортогональная) проекция наклонной перпендикулярна прямой на
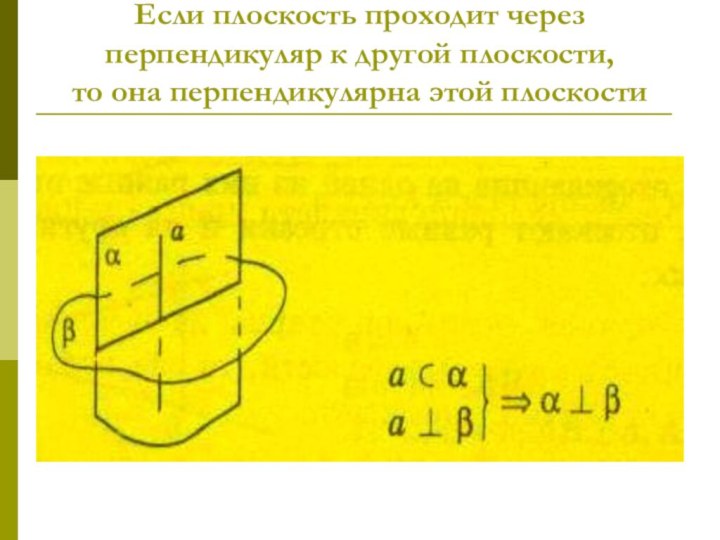
- 71. Если плоскость проходит через перпендикуляр к другой плоскости, то она перпендикулярна этой плоскости
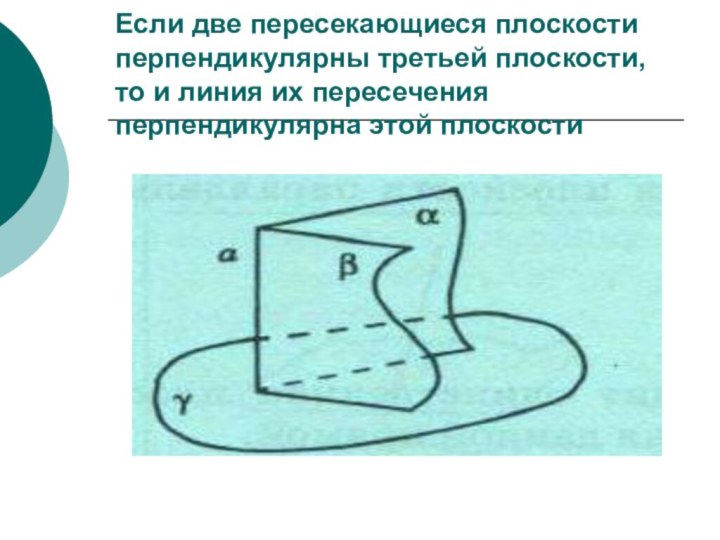
- 72. Если две пересекающиеся плоскости перпендикулярны третьей плоскости, то и линия их пересечения перпендикулярна этой плоскости
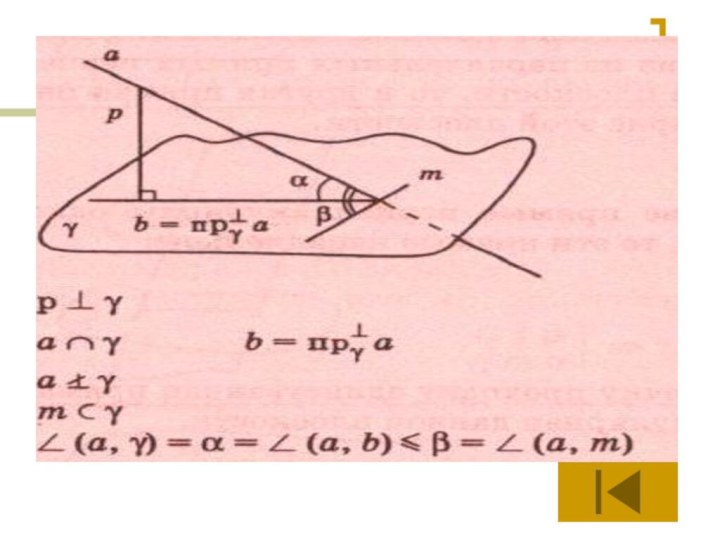
- 73. Угол, образованный наклонной и плоскостью, не больше
- 75. Контрольные работы и задания по карточкам
- 76. Карточка 1Точки A, B, C, D не
- 77. Карточка 2Точки K, L, M, T не
- 78. Карточка 3Прямые b и c пересекаются. Прямая
- 79. Карточка 4Прямые а и b пересекаются. Прямая
- 80. Карточка 1Через точки А и В проведены
- 81. Карточка 2Через точки М и К проведены
- 82. Карточка 3Телефонная проволока длиной 10 м. протянута
- 83. Карточка 4Телефонная проволока длиной 10 м. протянута
- 84. Карточка 1Точка отстоит от плоскости на 12
- 85. Карточка 2Точка отстоит от плоскости на 8
- 86. Параллельность прямых и плоскостей№ 1Через концы отрезка
- 87. № 2Плоскость β проходит через основание КL
- 88. № 3Даны параллельные плоскости β и γ.
- 89. № 4Докажите, что все прямые, пересекающие две данные параллельные прямые, лежат в одной плоскости.
- 90. № 5Параллельные прямые а и b пересекают
- 91. Перпендикулярность прямых и плоскостей. № 11. Через
- 92. № 2 Точка А отстоит от плоскости
- 93. № 3Дан прямоугольник АВСД. Через точку О
- 94. Вопросы1) Как называется раздел геометрии, изучающий фигуры
- 95. Скачать презентацию
- 96. Похожие презентации
Взаимное расположение точек, прямых и плоскостей в простанстве






















































Слайд 9
Две прямые в
пространстве
Две прямые в
пространстве
Лежат в
одной
плоскости
Совпадают
Не лежат в
одной плоскости
Не имеют общих
точек(параллельны)
Пересекаются
(в одной точке)
Скрещиваются
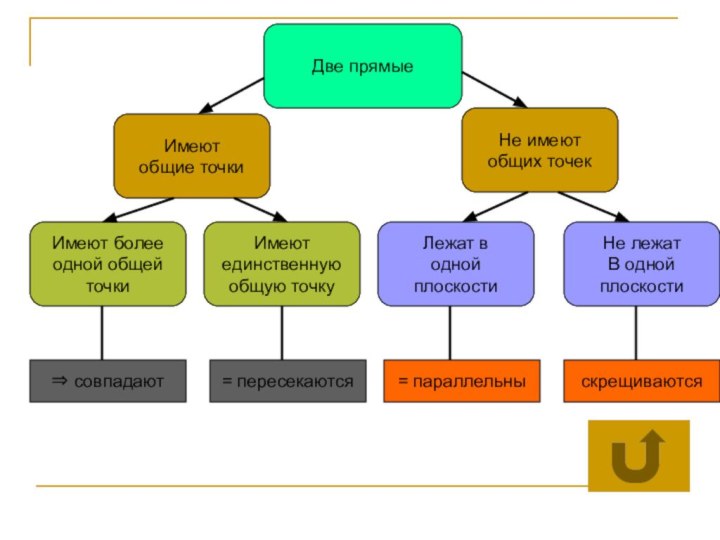
Слайд 10
Имеют
единственную
общую точку
Имеют
единственную
общую точку
Имеют более
одной общей
точки
Лежат в
одной плоскости
Не лежат
В одной
плоскости
Имеют
общие точки
Не имеют
общих точек
Две прямые
⇒ совпадают
= пересекаются
= параллельны
скрещиваются
Слайд 21
Прямая называется
параллельной плоскости,
а плоскость –
параллельной
прямой,
если они не имеют общих точек.
Слайд 27
Прямая, все точки которой принадлежат плоскости, называется прямой,
лежащей в этой плоскости.
Слайд 33
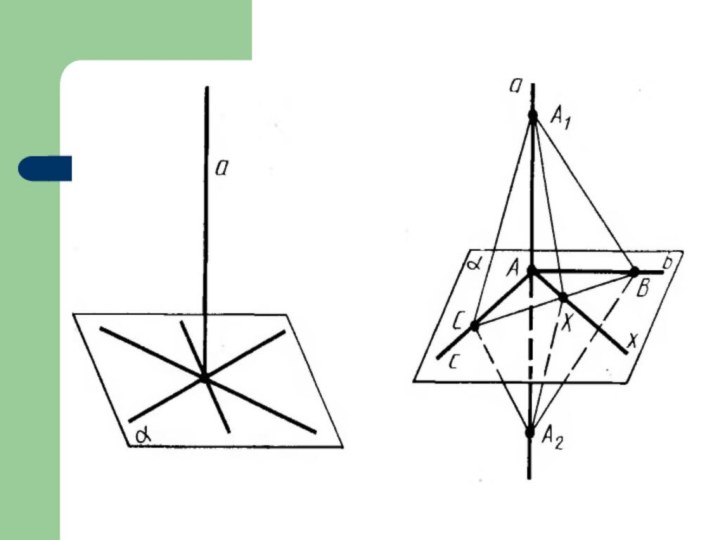
Прямая называется перпендикулярной плоскости (а плоскость прямой), если
прямая перпендикулярна любой прямой лежащей в этой плоскости.
Слайд 34
ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ
Если прямая перпендикулярна двум
пересекающимся прямым,
лежащим в плоскости, то она перпендикулярна данной
плоскости.
Слайд 36
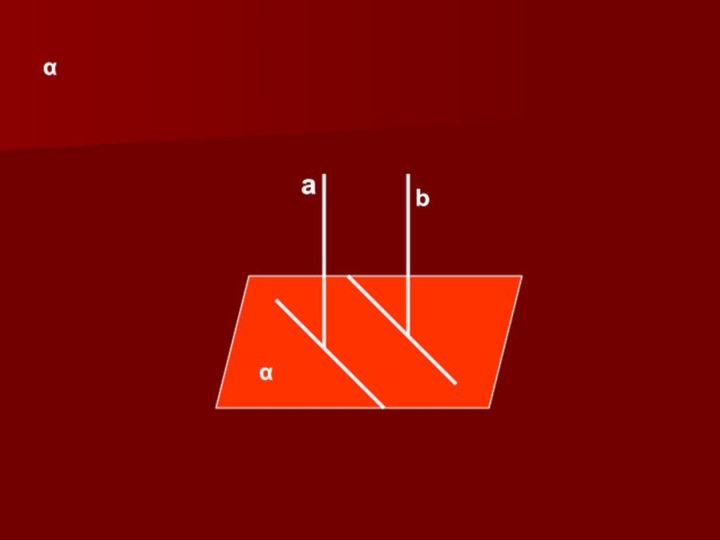
СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ
Если плоскость перпендикулярна одной
из двух параллельных прямых, то она перпендикулярна и другой.
Слайд 38
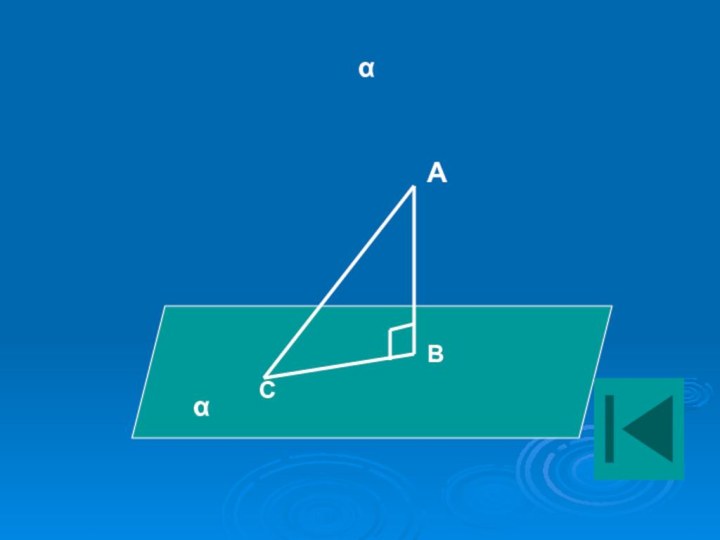
ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ
Перпендикуляром, опущенным из данной точки на
данную плоскость, называется отрезок, соединяющий данную точку с точкой
плоскости и лежащий на прямой, перпендикулярной плоскости.
Слайд 39
Наклонной, проведенной из данной точки к данной плоскости,
называется любой отрезок, соединяющий данную точку с точкой плоскости,
не являющийся перпендикуляром к плоскости.
Слайд 41
Двугранным углом
называется фигура, образованная двумя полуплоскостями с
общей ограничивающей их прямой. Полуплоскости называются гранями, а ограничивающая
их прямая — ребром двугранного угла.
Слайд 43
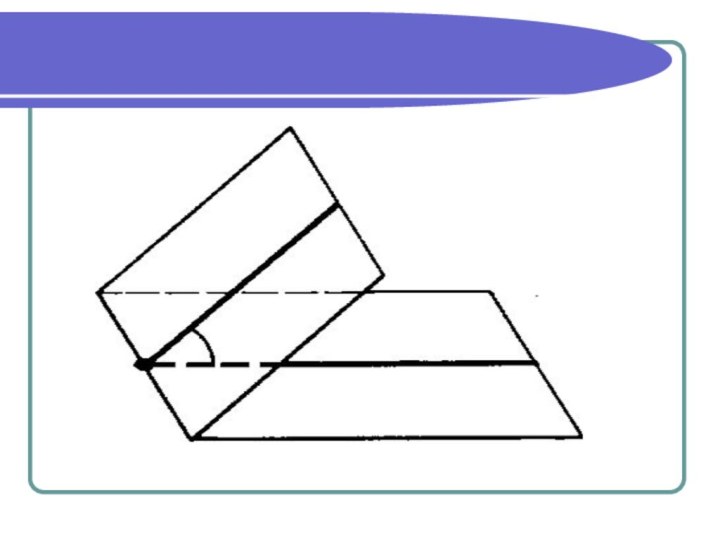
Линейным углом двугранного
угла называется пересечение этого двугранного
угла и плоскости перпендикулярной его ребру.
Слайд 44
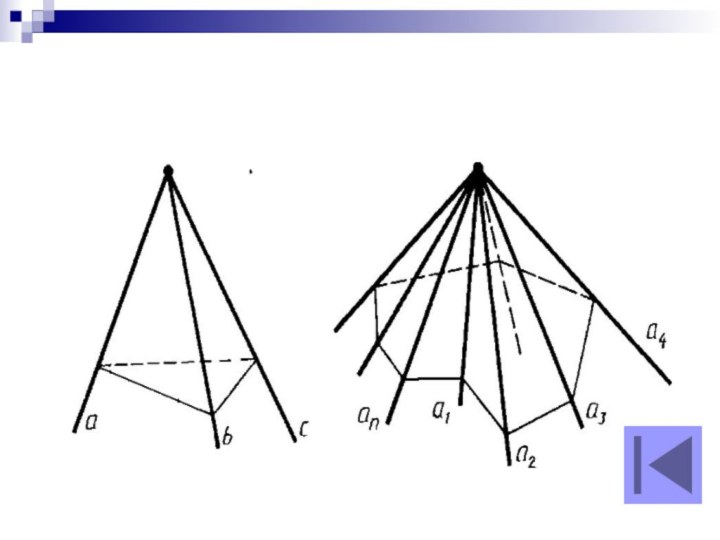
Трехгранным углом (аbс) называется фигура, составленная из трех
плоских углов (аb), (bс) и (ас). Эти углы называются
гранями трехгранного угла, а их стороны — ребрами. Общая вершина плоских углов называется вершиной трехгранного угла. Двугранные углы, образованные гранями трехгранного угла, называются двугранными углами трехгранного угла.
Слайд 46
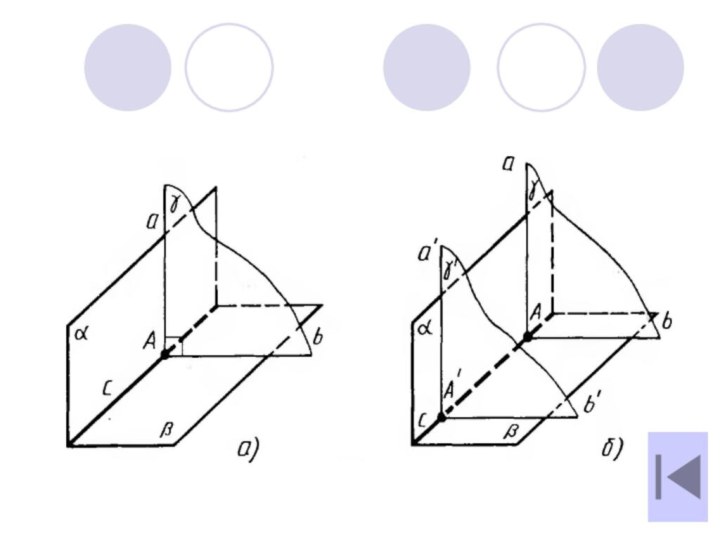
Две пересекающиеся плоскости называются перпендикулярными, если третья
плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по
перпендикулярным прямым.
Слайд 47
ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ
Если плоскость проходит через прямую, перпендикулярную
другой плоскости, то эти плоскости перпендикулярны.
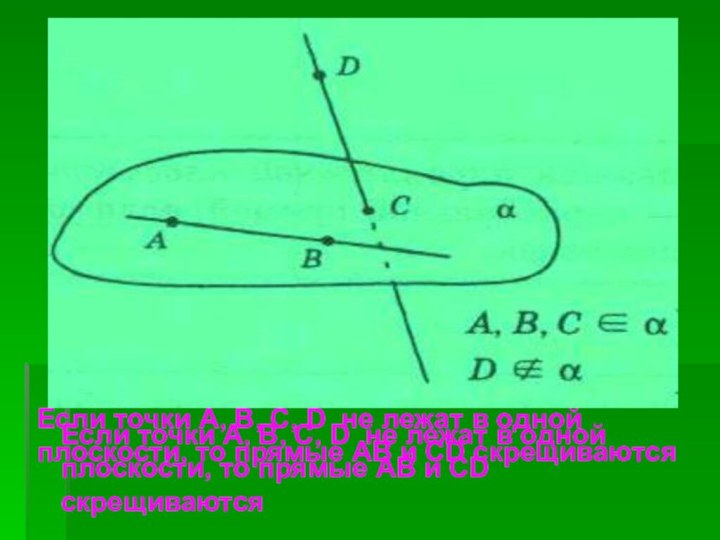
Слайд 53 Если точки A, B, C, D не лежат
в одной плоскости, то прямые AB и CD скрещиваются
Если
точки A, B, C, D не лежат в одной плоскости, то прямые AB и CD скрещиваютсяСлайд 54 Если одна из параллельных прямых пересекает плоскость, то
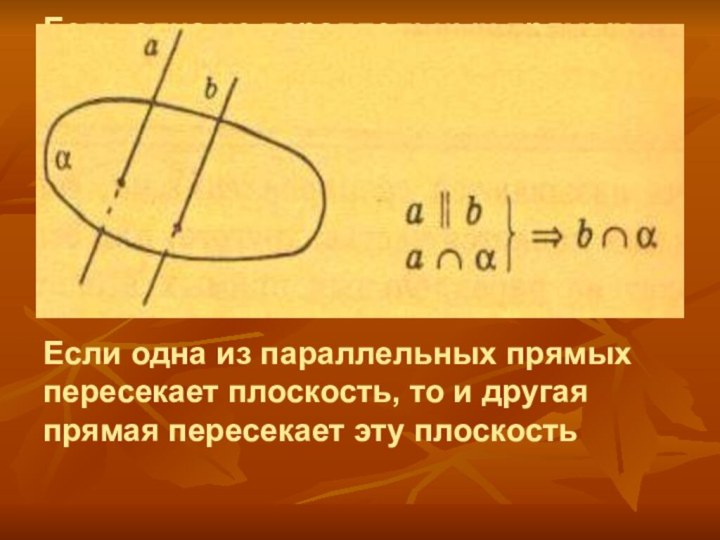
и другая прямая пересекает эту плоскость
Если одна из параллельных
прямых пересекает плоскость, то и другая прямая пересекает эту плоскость
Слайд 55
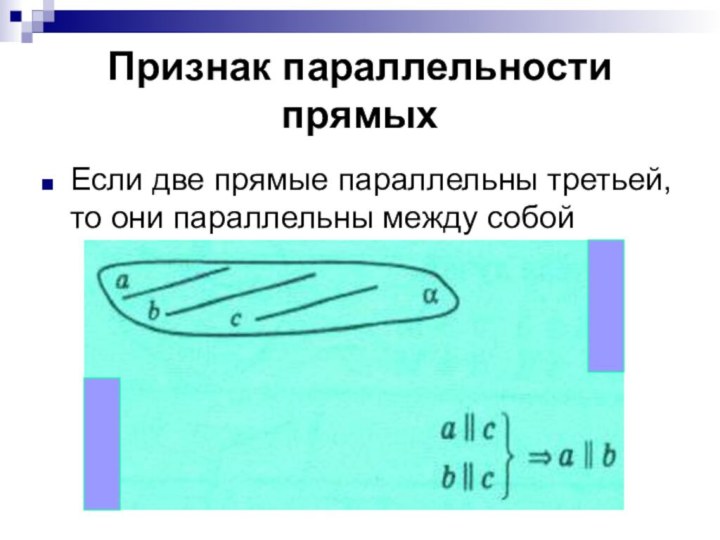
Признак параллельности прямых
Если две прямые параллельны третьей, то
они параллельны между собой
Слайд 56
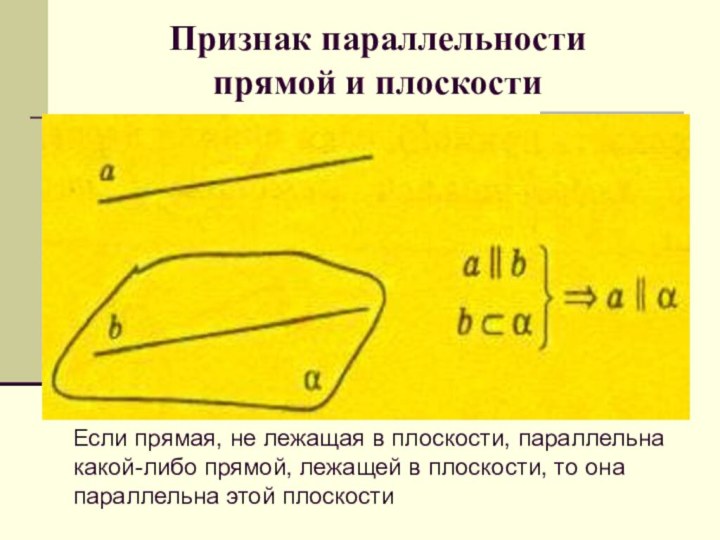
Признак параллельности
прямой и плоскости
Если прямая, не лежащая
в плоскости, параллельна какой-либо прямой, лежащей в плоскости, то
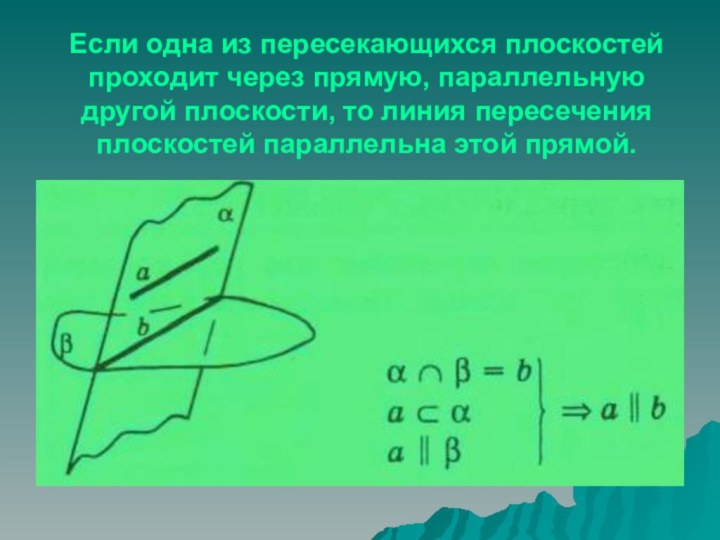
она параллельна этой плоскостиСлайд 57 Если одна из пересекающихся плоскостей проходит через прямую,
параллельную другой плоскости, то линия пересечения плоскостей параллельна этой
прямой.
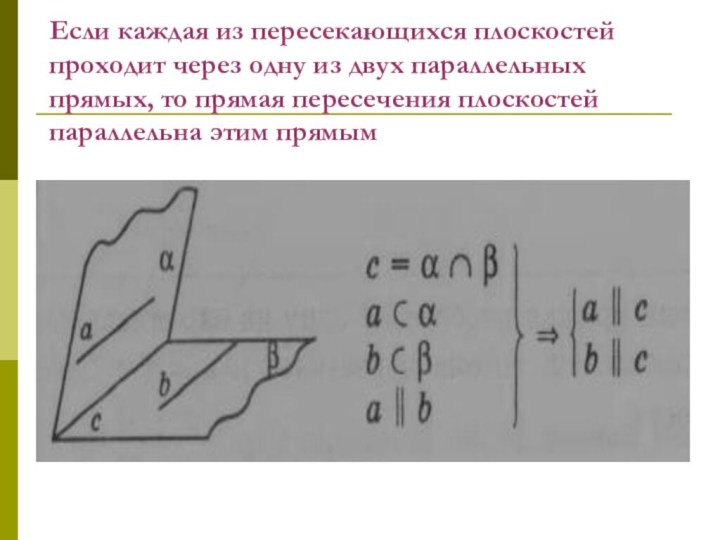
Слайд 58 Если каждая из пересекающихся плоскостей проходит через одну
из двух параллельных прямых, то прямая пересечения плоскостей параллельна
этим прямым
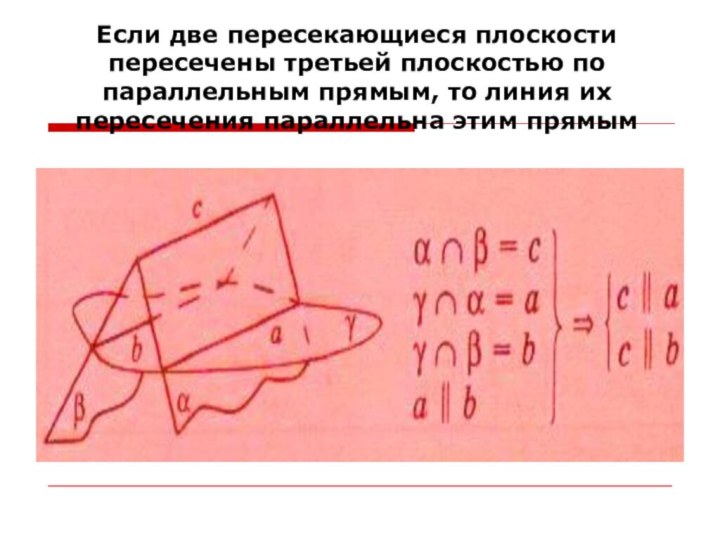
Слайд 59 Если две пересекающиеся плоскости пересечены третьей плоскостью по
параллельным прямым, то линия их пересечения параллельна этим прямым
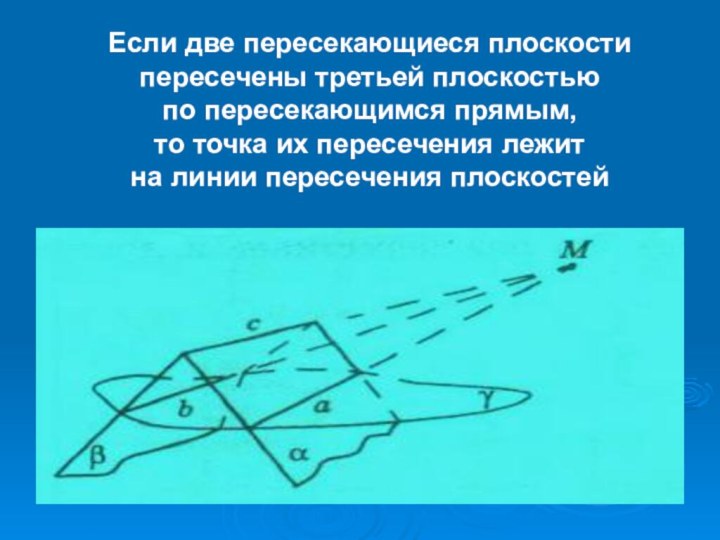
Слайд 60 Если две пересекающиеся плоскости пересечены третьей плоскостью по
пересекающимся прямым, то точка их пересечения лежит на линии
пересечения плоскостей
Слайд 62 Если две пересекающиеся прямые одной плоскости соответственно параллельны
двум пересекающимся прямым другой плоскости, то эти плоскости параллельны
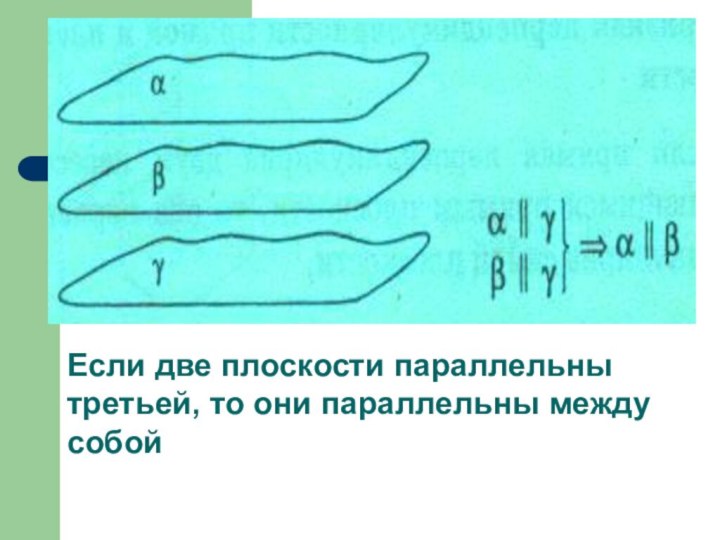
Слайд 63 Если две плоскости параллельны третьей, то они параллельны
между собой
Если две плоскости параллельны третьей, то они параллельны
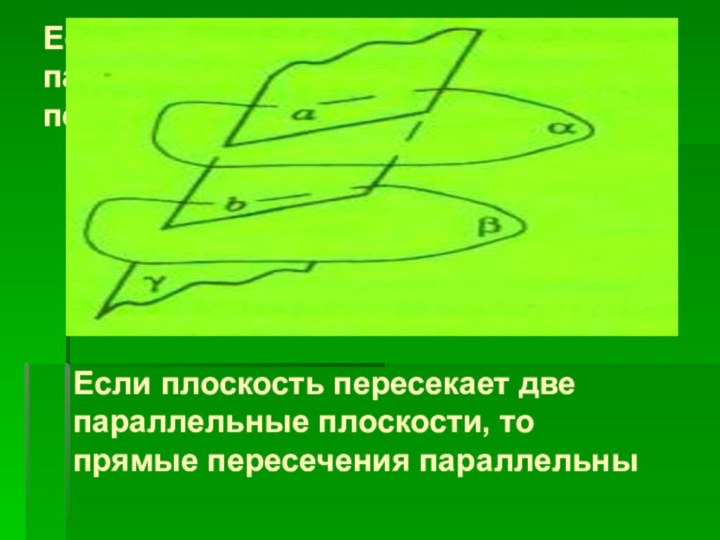
между собойСлайд 65 Если плоскость пересекает две параллельные плоскости, то прямые
пересечения параллельны
Если плоскость пересекает две параллельные плоскости, то прямые
пересечения параллельныСлайд 66 Если прямая пересекает одну из параллельных плоскостей, то
она пересекает и другую плоскость
Если прямая пересекает одну из
параллельных плоскостей, то она пересекает и другую плоскостьСлайд 67 Если плоскость пересекает одну из параллельных плоскостей, то
она пересекает и другую плоскость
Слайд 68 Через точку, не лежащую на плоскости, можно провести
одну и только одну плоскость, параллельную данной
Через точку, не
лежащую на плоскости, можно провести одну и только одну плоскость, параллельную данной
Слайд 69
Если (ортогональная) проекция наклонной перпендикулярна прямой на плоскости,
то и сама наклонная перпендикулярна этой прямой.
Если наклонная перпендикулярна
некоторой прямой плоскости, то и (ортогональная) проекция наклонной на эту плоскость перпендикулярна этой прямой.Теорема о трех перпендикулярах
Слайд 71 Если плоскость проходит через перпендикуляр к другой плоскости,
то она перпендикулярна этой плоскости
Слайд 72 Если две пересекающиеся плоскости перпендикулярны третьей плоскости, то
и линия их пересечения перпендикулярна этой плоскости
Слайд 73
Угол, образованный наклонной и плоскостью, не больше угла
между этой наклонной и любой прямой плоскости.
Углом между наклонной
и плоскостью называется угол между наклонной и ее ортогональной проекцией на эту плоскость.
Слайд 76
Карточка 1
Точки A, B, C, D не лежат
в одной плоскости. Могут ли прямые AB и CD
пересекаться?Через точки K, L и середину N отрезка KL проведены параллельные прямые, пересекающие некоторую плоскость α в точках K1, L1, N1 соответственно. Найдите длину отрезка NN1, если KK1 = 15 м, LL1 = 5 м, причем отрезок KL не пересекает плоскость α.
Слайд 77
Карточка 2
Точки K, L, M, T не лежат
в одной плоскости. Могут ли прямые KL и MT
пересекаться?Через точки A, B и середину N отрезка AB проведены параллельные прямые, пересекающие некоторую плоскость α в точках A1, B1, N1 соответственно. Найдите длину отрезка NN1, если AA1 = 10 м, BB1 = 8 м, причем отрезок AB не пересекает плоскость α.
Слайд 78
Карточка 3
Прямые b и c пересекаются. Прямая f
является скрещивающейся с прямой b. Могут ли прямые с
и f быть параллельными? Ответ обоснуйте.Плоскость β проходит через середины боковых сторон AB и CD трапеции ABCD – точки S и P. Докажите, что AD || β. Найдите BC, если AD=6 м, SP =9 м.
Слайд 79
Карточка 4
Прямые а и b пересекаются. Прямая k
является скрещивающейся с прямой а. Могут ли прямые b
и k быть параллельными? Ответ обоснуйте.Плоскость β проходит через середины боковых сторон AB и CD трапеции ABCD – точки S и P. Докажите, что AD || β. Найдите BC, если AD=12 см, SP =10см.
Слайд 80
Карточка 1
Через точки А и В проведены прямые,
перпендикулярные плоскости β, пересекающие её в точках С и
D соответственно. Найдите расстояние между точками А и В, если АС = 8 см, ВD= 5 см, СD= 4 см и отрезок АВ не пересекает плоскость β.
Слайд 81
Карточка 2
Через точки М и К проведены прямые,
перпендикулярные плоскости α, пересекающие её в точках Т и
L соответственно. Найдите расстояние между точками М и К, если МТ= 12 см, КL = 8 см, ТL = 3 см и отрезок МК не пересекает плоскость α.
Слайд 82
Карточка 3
Телефонная проволока длиной 10 м. протянута от
телефонного столба, где она прикреплена на высоте 12 м.
от поверхности земли, к дому, где её прикрепили на высоте 18 м. Найдите расстояние между домом и столбом, предполагая, что проволока не провисает.
Слайд 83
Карточка 4
Телефонная проволока длиной 10 м. протянута от
телефонного столба, где она прикреплена на высоте 14 м.
от поверхности земли, к дому, где её прикрепили на высоте 22 м. Найдите расстояние между домом и столбом, предполагая, что проволока не провисает.
Слайд 84
Карточка 1
Точка отстоит от плоскости на 12 см;
из неё проведена к плоскости наклонная, равная 13 см.
Чему равна проекция этой плоскости?CDEK – квадрат, диагональ которого равна 8 см. BD перпендикулярно плоскости CDE. Найдите расстояние от точки B до плоскости CDE, BK=10 см.
Слайд 85
Карточка 2
Точка отстоит от плоскости на 8 см;
из неё проведена к плоскости наклонная, равная 10 см.
Чему равна проекция этой плоскости?CDEK – квадрат, диагональ которого равна 12 см. BD перпендикулярно плоскости CDE. Найдите расстояние от точки B до плоскости CDE, BK=13 см.
Слайд 86
Параллельность прямых и плоскостей
№ 1
Через концы отрезка СD
и его середину К проведены параллельные прямые, пересекающие некоторую
плоскость в точках С1, D1 и К1.Найдите длину отрезка КК1, если отрезок СD не пересекает плоскость и СС1=8 см, DD1=10 см.СС1=10 см, DD1=12 см.(второй вариант)
Слайд 87
№ 2
Плоскость β проходит через основание КL трапеции
КМNL. А и В – середины боковых сторон трапеции.
Докажите, что АВ||β. Найдите КL, если МN=5 см, АВ = 7 см.МN=7 см, АВ = 9 см. (второй вариант)
Слайд 88
№ 3
Даны параллельные плоскости β и γ. Через
точки С и D плоскости проведены параллельные прямые, пересекающие
плоскость γ в точках С1 и D1. Найдите С1D1, если СD=9 см.СD=10 см. (второй вариант)
Слайд 89
№ 4
Докажите, что все прямые, пересекающие две данные
параллельные прямые, лежат в одной плоскости.
Слайд 90
№ 5
Параллельные прямые а и b пересекают одну
из двух параллельных плоскостей в точках А1 и В1,
а другую в точках А2 и В2 соответственно. Найдите <А2А1В1, если <А1А2В2 = 140°<А1А2В2 = 150°(второй вариант)
Слайд 91
Перпендикулярность прямых и плоскостей. № 1
1. Через точки
А и В проведены прямые, перпендикулярные плоскости α, пересекающие
её в точках Си Д соответственно. Найдите расстояние между точками А и В, если отрезок АВ не пересекает плоскость α и АС = 10 см, ВД = 4 см, СД = 8 см.(Второй вариант: АС = 10 см, ВД = 2 см, СД = 6 см.)
Слайд 92
№ 2
Точка А отстоит от плоскости на
расстояние 4 м. Найти длину наклонной, проведенной из этой
точки под углом 30° к плоскости.(Второй вариант: Точка А отстоит от плоскости на расстояние 6 м.)
Слайд 93
№ 3
Дан прямоугольник АВСД. Через точку О пересечения
его диагоналей проведена прямая ОК, перпендикулярная его плоскости. Найдите
расстояние от т. К до вершин прямоугольника, если ОК =24 см, АВ =12 см, АД =16 см.
Слайд 94
Вопросы
1) Как называется раздел геометрии, изучающий фигуры в
пространстве?
2) Как называется раздел геометрии, изучающий фигуры на плоскости?
3)
Назовите основные фигуры в пространстве?4) Могут ли прямая и плоскость иметь две общие точки?
5) Сколько плоскостей можно провести через три точки?
6) Сколько плоскостей можно провести через прямую и не лежащую на ней точку?
7) Сколько может быть общих точек у прямой и плоскости?
8) Могут ли прямая и плоскость иметь одну общую точку?