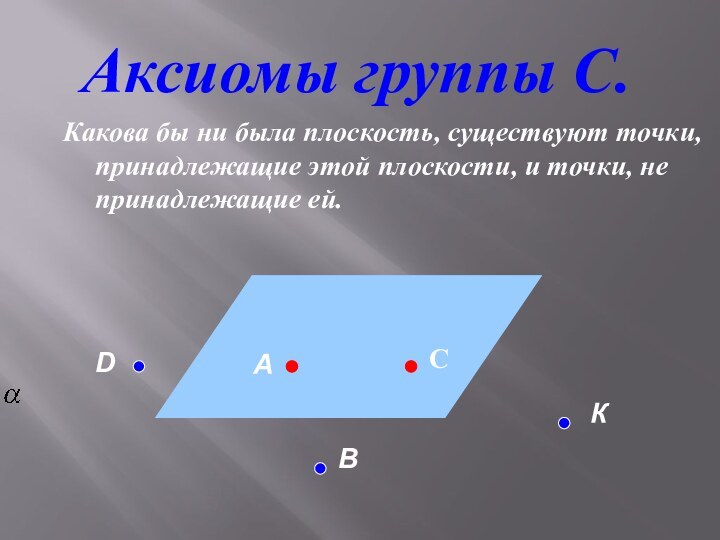
плоскость, существуют точки, принадлежащие этой плоскости, и точки, не
принадлежащие ей.
А
К
D
B
С
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть



















А
К
D
B
С
С
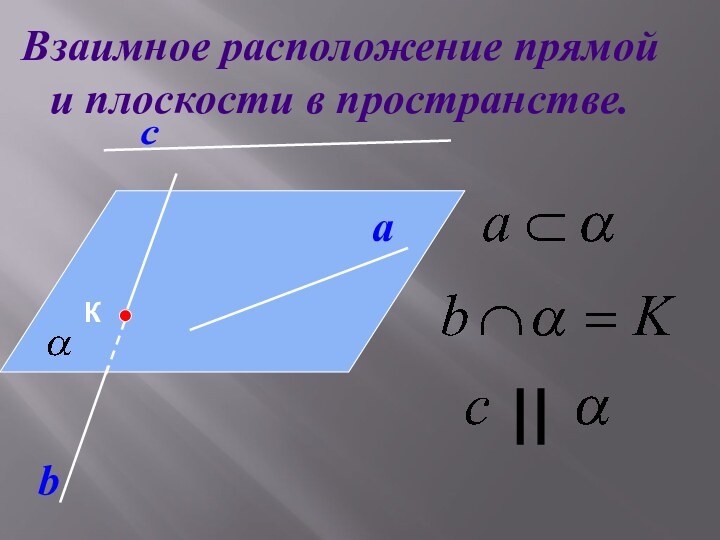
с
a
b
С
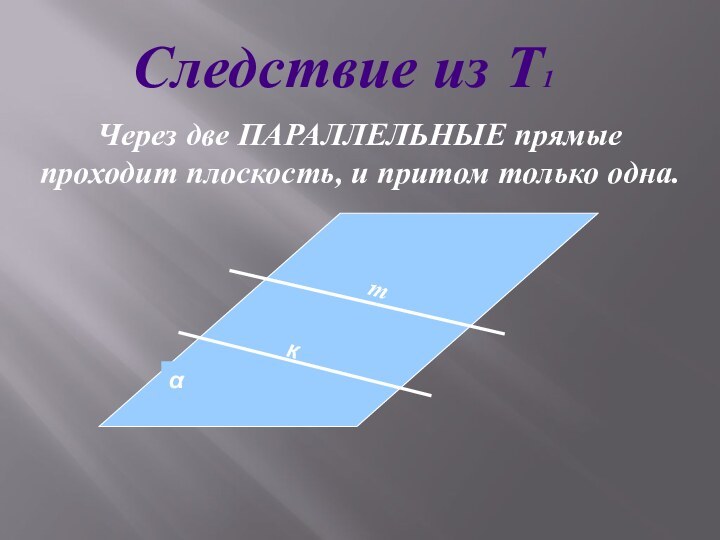
Т1
4. По двум параллельным прямым.
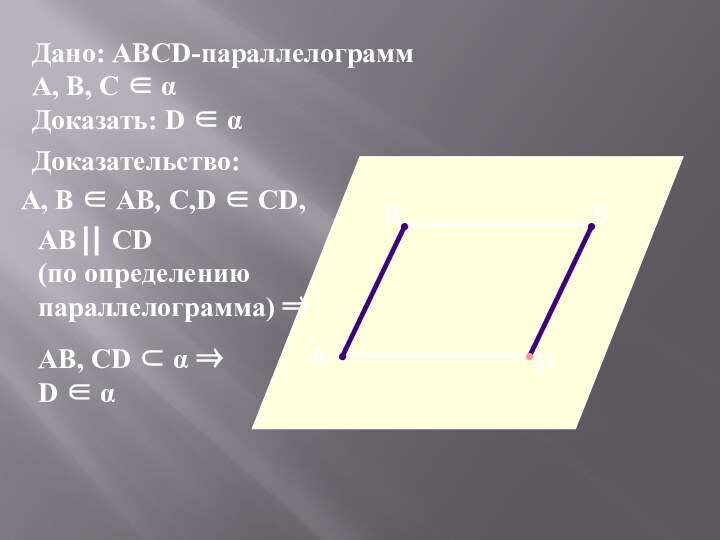
АВ СD
(по определению параллелограмма)
АВ, СD α
D α
1. Возьмем т.В, В в
Через т.В и с проведем плоскость
α = в1
2. Если в1 β = Х, Х а, в1 α,
но Х с, т.к. в1 , а т.к. а с в1 β
3. в1 α, в1 а в1 а в1 = в (А параллельных прямых)
4. в с
Теорема доказана.
•
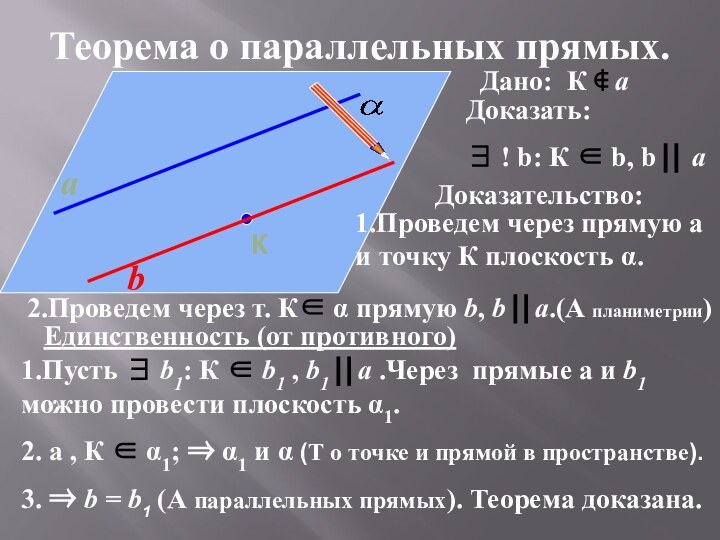
Две прямые, параллельные третьей прямой, параллельны
2.Проведем через т. К α прямую b, b a.(А планиметрии)
Единственность (от противного)
1.Пусть b1: К b1 , b1 a .Через прямые a и b1 можно провести плоскость α1.
2. a , К α1; α1 и α (Т о точке и прямой в пространстве).
3. b = b1 (А параллельных прямых). Теорема доказана.
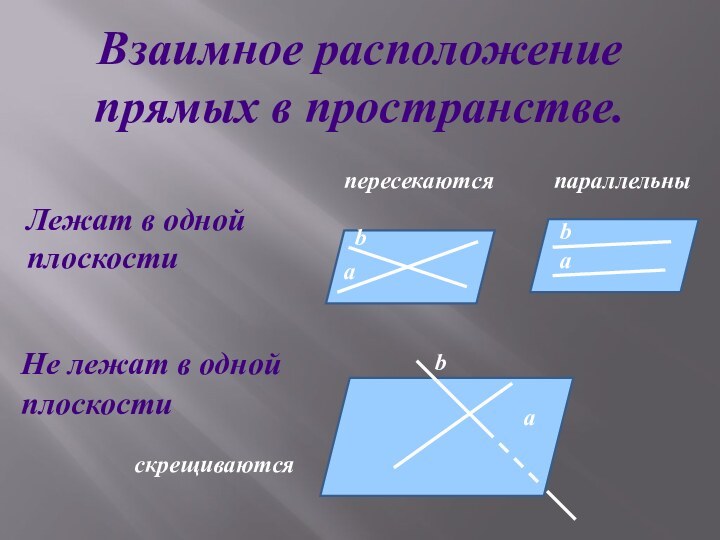
α, то прямые а и b
не лежат
две
прямую
параллельными
лежат
скрещивающиеся
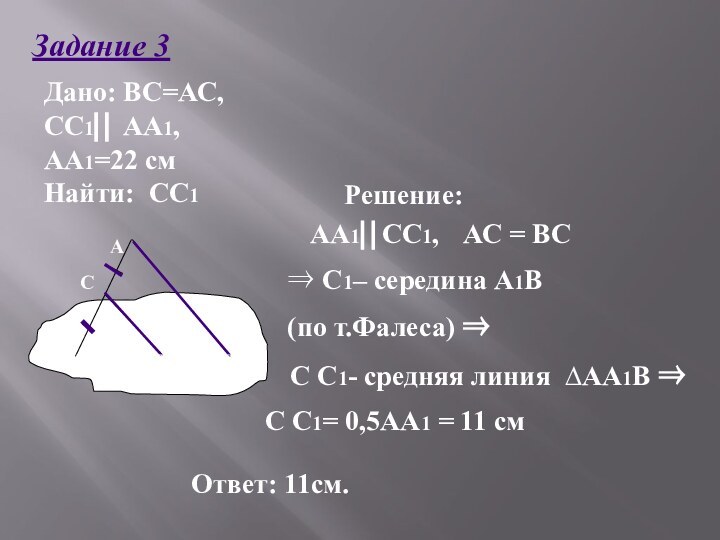
С С1- средняя линия ∆АА1В
С С1= 0,5АА1 = 11 см
Ответ: 11см.
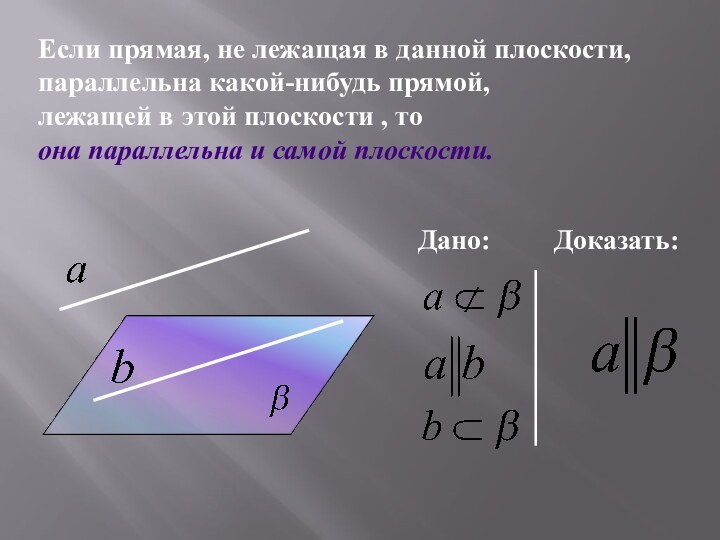
Дано:
Доказать:
α
2. α β = b
Если a β = Х, то Х b, это невозможно, т.к. α b
a β
a β
Теорема доказана.
Задание 2
α
β
а
в
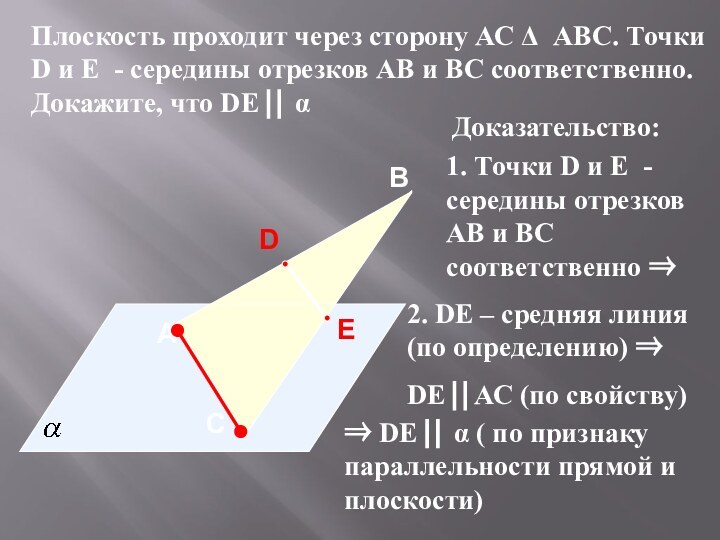
Доказательство:
1. Точки D и E - середины отрезков АВ и BC соответственно
2. DE – средняя линия (по определению)
DE АС (по свойству)
DE α ( по признаку параллельности прямой и плоскости)
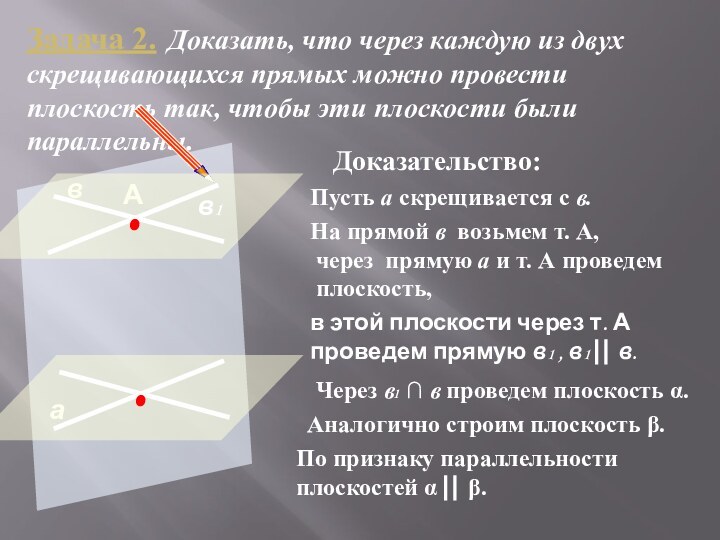
Дано: а b = M, a , b .
a₁ b₁, a₁ , b₁ . a a₁, b b₁.
Доказать:
а
а₁
b
b₁
M
c
Доказательство:
Тогда а , а , = с, значит а с.
2. b , b , = с, значит b с.
3. Имеем, что через точку М проходят две прямые а и b, параллельные прямой с, чего быть на может.
Значит .
1. Пусть = с.
существует плоскость β║α, проходящая через точку А
1. В плоскости α проведём прямые а∩в.
Через точку А проведём
а1║а
и в1║в.
По признаку параллельности плоскостей прямые а1 и в1 задают плоскость β║α.
Существование плоскости β доказано.
Отметим в плоскости β1 т. С β.
Отметим произвольную т. В α.
Через точки А, В и С проведем γ.
γ ∩ α = в,
γ ∩ β1 = с.
γ ∩ β = а,
а
а и с не пересекают плоскость α,
значит они не пересекают прямую в,
а в и с в
Получили, что через т. А проходят две прямые, параллельные прямой в, чего быть не может.
наше предположение ложное.
Единственность β доказана.
Доказать: a b
Доказательство:
1. a , b
2. Пусть a b,
тогда a b = М
3. M α, M β
α β = с (А2)
Получили противоречие с условием.
Значит a b ч. т.д.
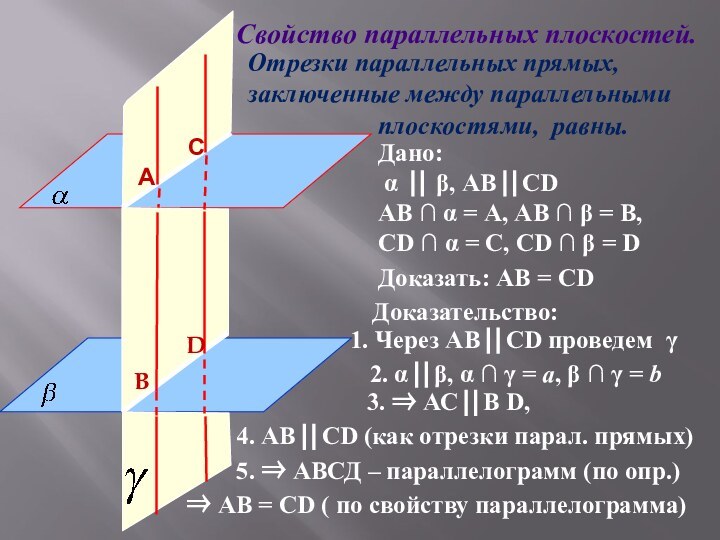
Доказать: АВ = СD
Дано:
α β, АВ СD
АВ α = А, АВ β = В,
СD α = С, СD β = D
Доказательство:
1. Через АВ СD проведем
2. α β, α = a, β = b
3. АС В D,
4. АВ СD (как отрезки парал. прямых)
5. АВСД – параллелограмм (по опр.)
АВ = СD ( по свойству параллелограмма)
ДА
НЕТ
ДА
НЕТ
ДА
НЕТ
НЕТ
ДА
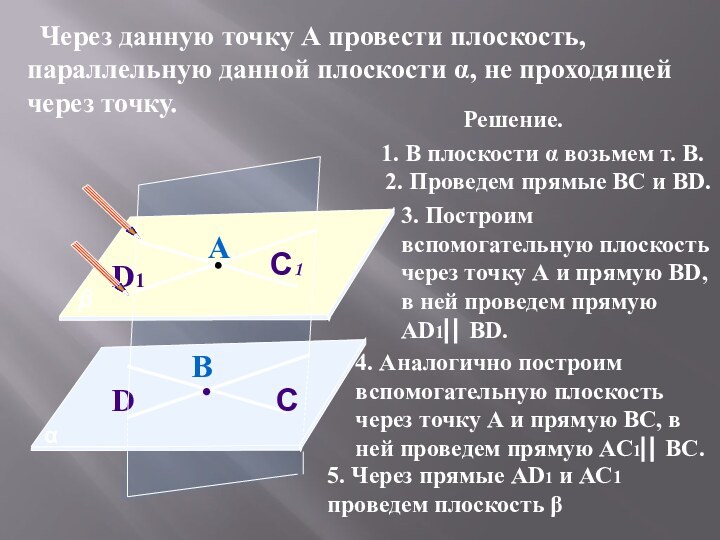
2. Проведем прямые ВС и ВD.
В
•
С1
D1
D
С
3. Построим вспомогательную плоскость через точку А и прямую ВD, в ней проведем прямую АD1 ВD.
4. Аналогично построим вспомогательную плоскость через точку А и прямую ВС, в ней проведем прямую АС1 ВС.
•
5. Через прямые АD1 и АС1 проведем плоскость β