FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть
Об аксиомах геометрии
А на чём основаны доказательства самых первых теорем геометрии?
На аксиомах
Утверждениях о свойствах геометрических фигур, которые принимаются в качестве исходных положений ( без доказательства)
2.
?
1.
3.
Строится вся геометрия
365 – 300 гг. до н.э.
Геометрия, изложенная в «Началах», называется евклидовой геометрией
Некоторые из аксиом Евклида (часть из них он называл постулатами) и сейчас используются в геометрии
Слово «аксиома» происходит от греческого «аксиос», что означает «ценный, достойный».
Можно ли через т.М провести еще одну прямую , параллельную прямой а ?
в
Нам представляется, что через т.М нельзя провести прямую (отличную от прямой в), параллельную прямой а.
Можно ли это утверждение доказать?
Ответ на этот непростой вопрос дал великий русский математик
2.Если две прямые параллельны третьей прямой, то они параллельны.
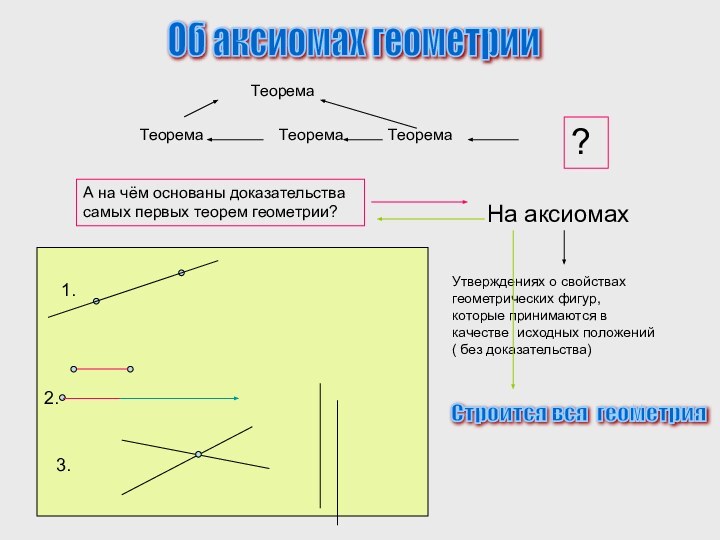
Следствия из аксиомы параллельных прямых
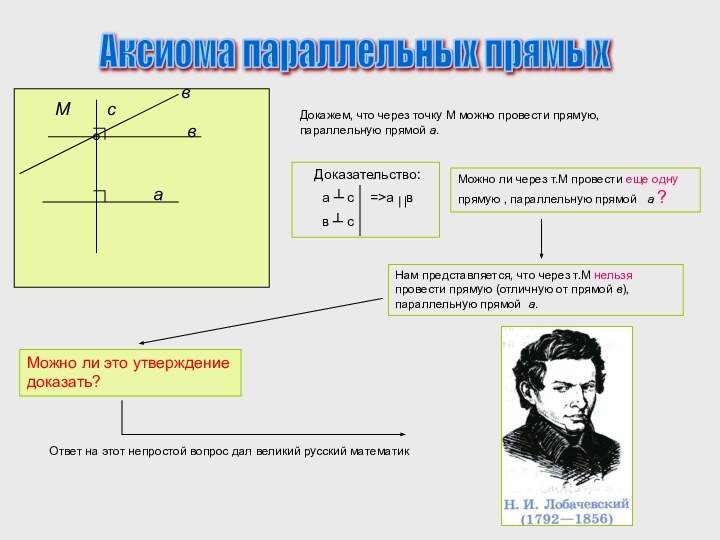
а
в
М
с
Доказательство:
Предположим, что прямая с не пересекает прямую в, значит, с в.
Тогда через т.М проходят две прямые а и с параллельные прямой в.
3. Но это противоречит аксиоме параллельных прямых, значит, прямая с пересекает прямую в.
а
в
с
Доказательство:
Предположим, что прямая а и прямая в пересекаются.
2. Тогда через т.М проходят две прямые а и в параллельные прямой с
3 . Но это противоречит аксиоме параллельных прямых.
4. Значит прямые а и в параллельны.
Способ рассуждения,, который называется
методом доказательства от противного
