скрывается приключение мысли. Решить задачу – это значит пережить
приключение.В. Произволов
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть













В. Произволов
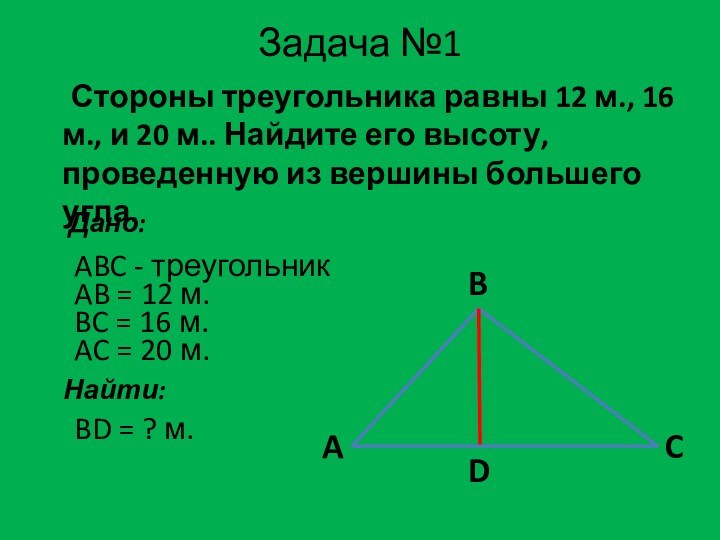
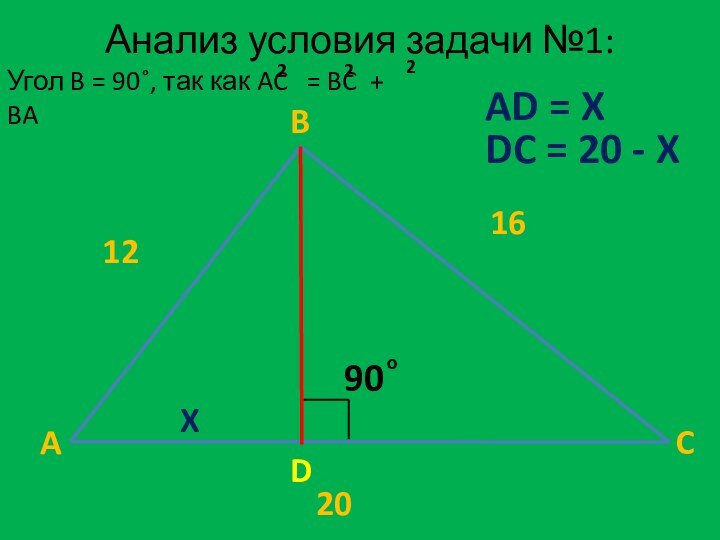
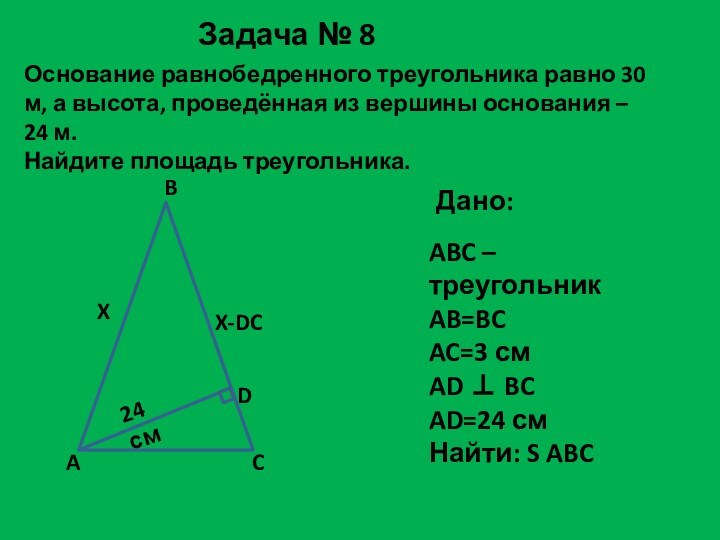
Дано:
A
B
C
ABC - треугольник
AB = 12 м.
BC = 16 м.
AC = 20 м.
Найти:
BD = ? м.
D
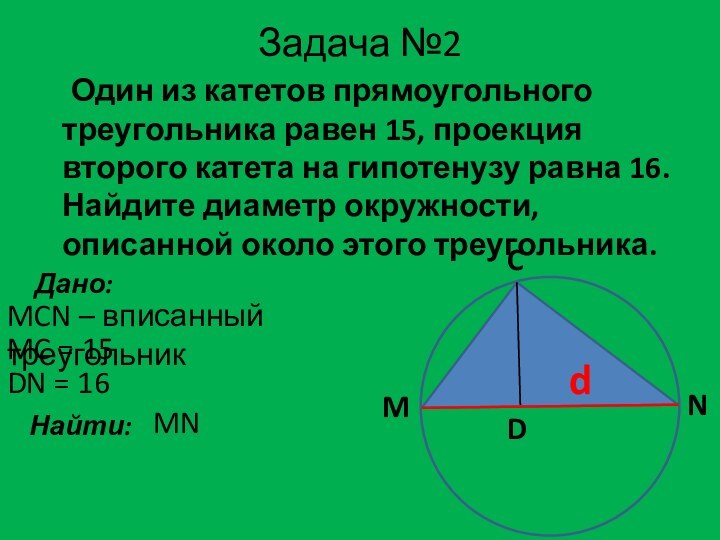
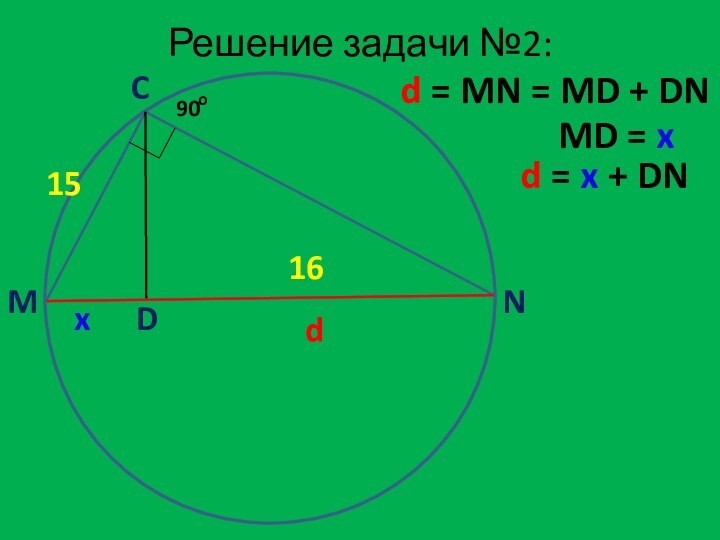
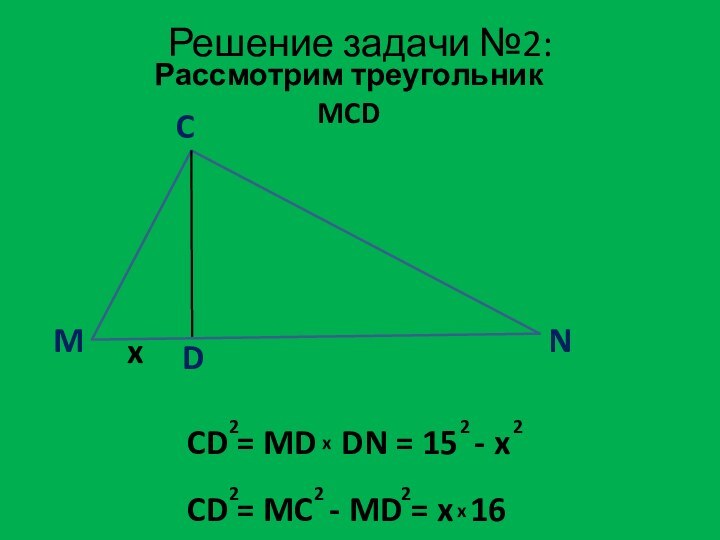
Дано:
MCN – вписанный треугольник
MC = 15
Найти:
MN
M
C
N
D
DN = 16
d
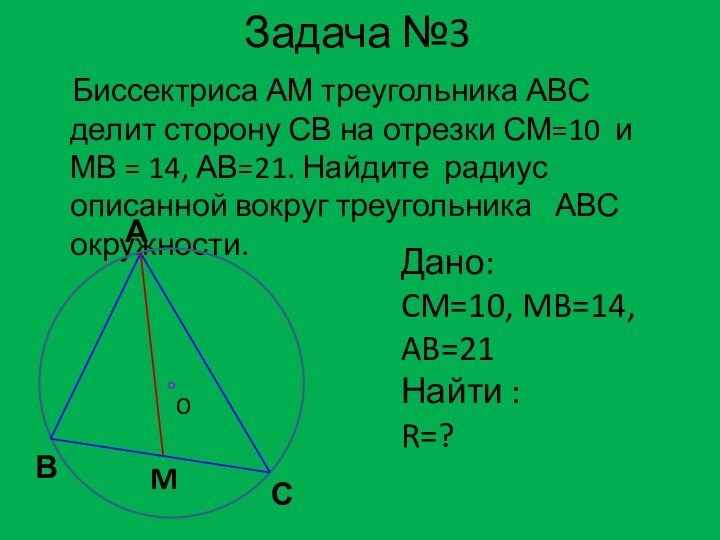
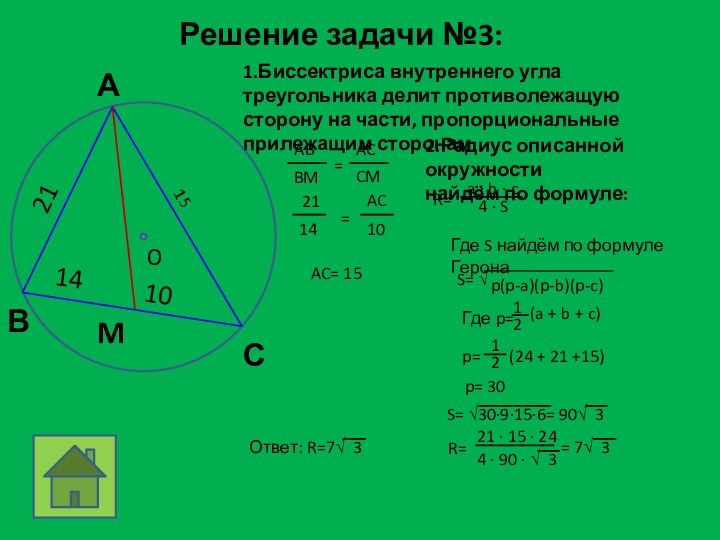
Дано:
CM=10, MB=14,
AB=21
Найти :
R=?
О – центр , вписанной окружности
6. AC = AH + HC = 14
21
Ответ : r = 4
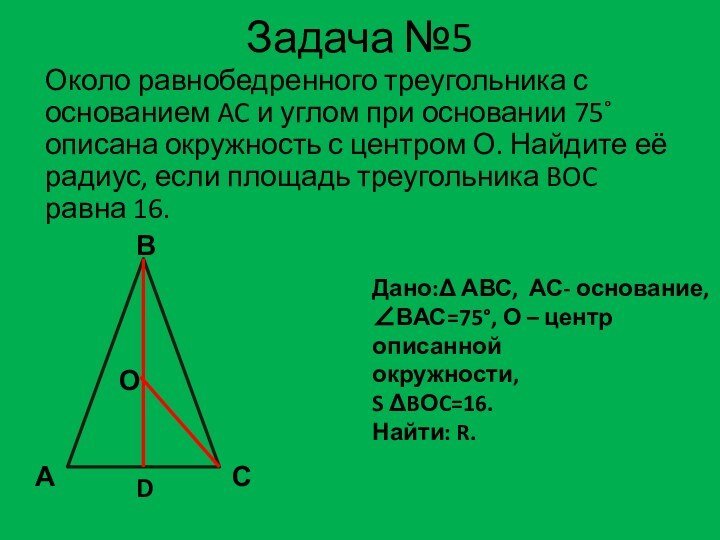
Дано: АВС, АС- основание,
ВАС=75, О – центр описанной
окружности,
S BОC=16.
Найти: R.
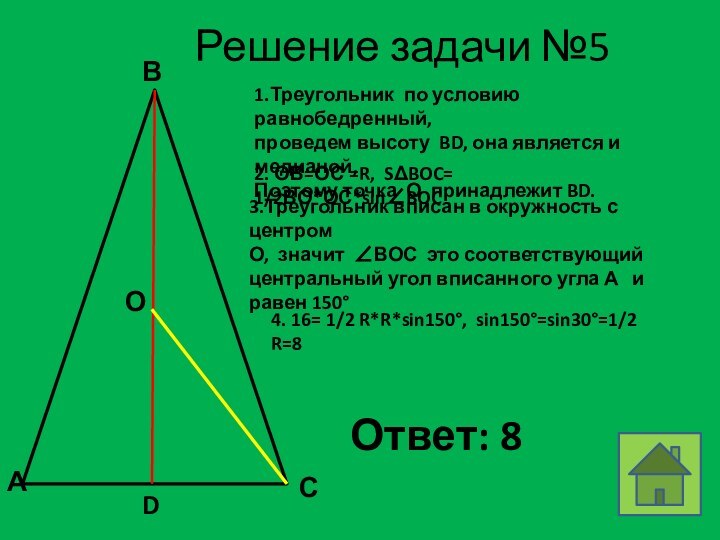
3.Треугольник вписан в окружность с центром
О, значит ВОС это соответствующий
центральный угол вписанного угла А и
равен 150
4. 16= 1/2 R*R*sin150, sin150=sin30=1/2
R=8
Ответ: 8
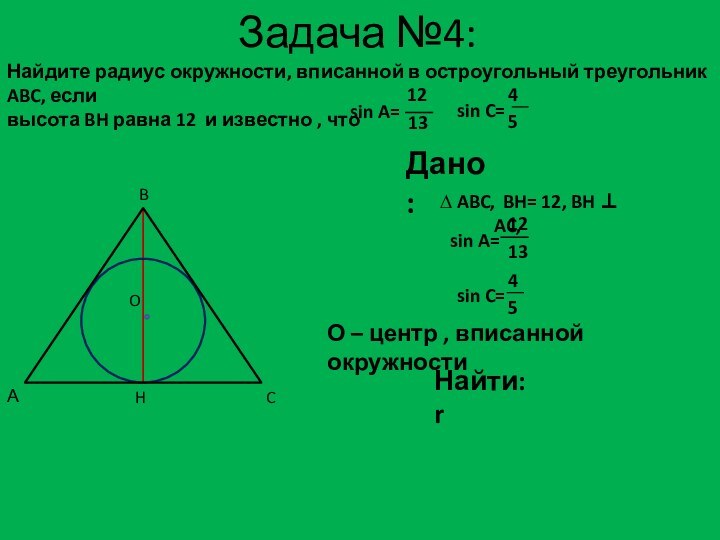
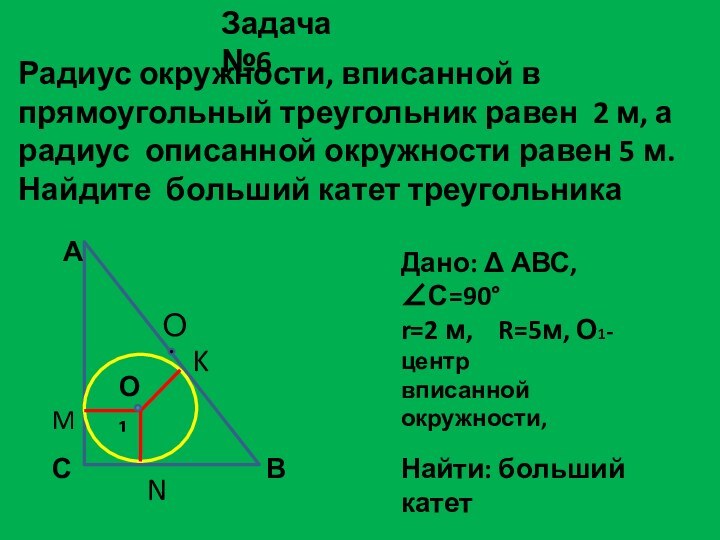
Задача №6
Дано: АВС, С=90
r=2 м, R=5м, О1- центр
вписанной окружности,
Найти: больший катет
3. Отрезки BK и BN равны как отрезки касательных,
проведенных из одной точки,
аналогично CN = CM;
AM = AK; обозначим BK = BN = x; тогда CB = 2 + x;
AK = AM = 10 – x; AC = 12 – x.
4. По т. Пифагора AB² = CB² + AC²; 10² = (2 + x)² + (12 –x)²
2x² - 20x + 48 = 0, x² - 10x = 24 = 0,
x₁ = 6, x₂ = 4;
AC = 12- 6 = 6; CB = 2 + 6 = 8м.
Ответ: 8м.
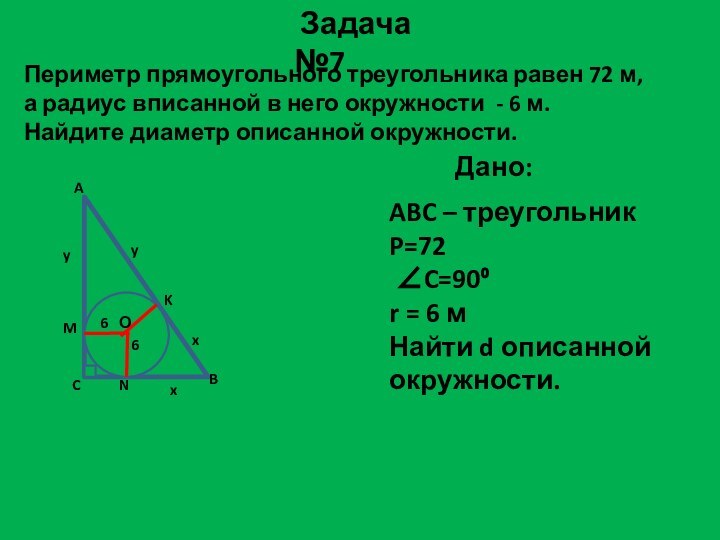
Дано:
ABC – треугольник
P=72
C=90⁰
r = 6 м
Найти d описанной окружности.
Задача №7
3. Обозначим отрезки BN = BK = x (OK AB)
OK=r , ВN=ВК как отрезки касательных AM = MK = y
P ∆АВС = AC + AB + CB, но
АС = 6+у, АВ = x + у СВ = 6+х
P ∆АВС = 6+у+х+у+6+х = 12+2х+2у = 72 (по условию)
х + у = (72-12) : 2 , х + у = 30 , АВ=30
Ответ : 30
ABC – треугольник
AB=BC
AC=3 см
AD BC
AD=24 см
Найти: S ABC
Задача № 8
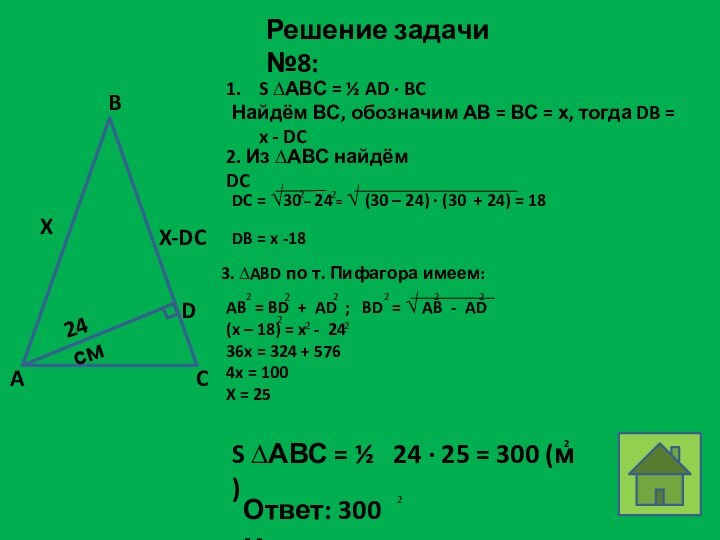
2. Из ∆АВС найдём DC
DB = x -18
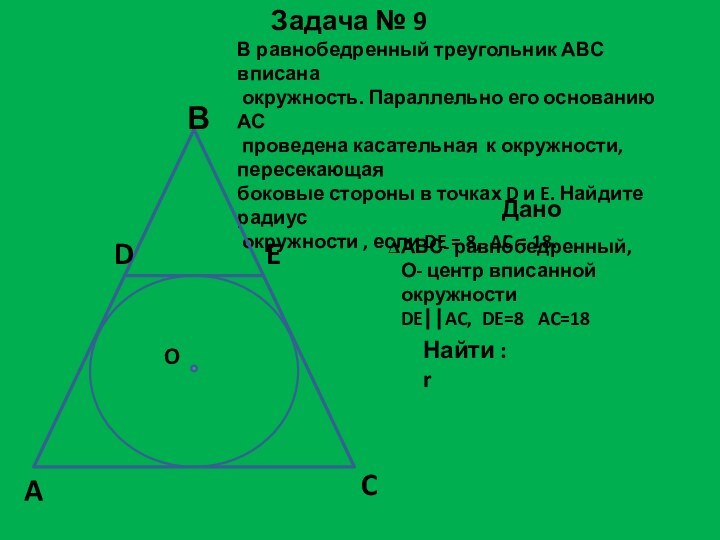
Дано:
АВС- равнобедренный,
О- центр вписанной окружности
DEAC, DE=8 AC=18
В
D
E
A
C
Найти : r
O
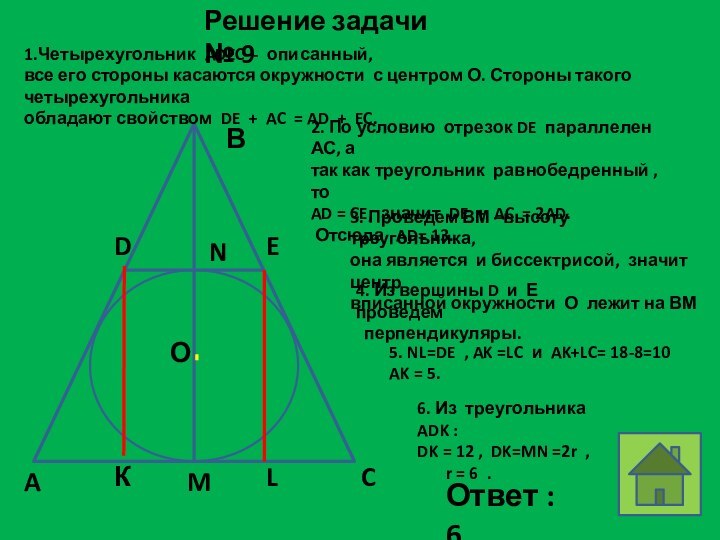
2. По условию отрезок DE параллелен АС, а
так как треугольник равнобедренный , то
AD = CE, значит DE + AC = 2AD.
Отсюда AD= 13.
3. Проведем ВМ –высоту треугольника,
она является и биссектрисой, значит центр
вписанной окружности О лежит на ВМ
4. Из вершины D и Е проведем
перпендикуляры.
К
L
6. Из треугольника ADK :
DK = 12 , DK=MN =2r ,
r = 6 .
5. NL=DE , AK =LC и AK+LC= 18-8=10
AK = 5.
Ответ : 6.
Фалес Пифагор
640/624 до н. э. прим. 570 до н. э.
Евклид II век до н. э.
Окружность, касающаяся всех трех сторон треугольника, называется его
вписанной окружностью
. Окружность, проходящая через все три вершины треугольника, называется его
описанной окружностью.
Биссектрисой треугольника, проведенной из данной вершины, называют
отрезок, соединяющий эту вершину с точкой на противоположной стороне и
делящий угол при данной вершине пополам.
Биссектрисы треугольника пересекаются в одной точке, и эта точка совпадает с центром вписанной окружности.
В равнобедренном треугольнике биссектриса, медиана и высота, проведенные
к основанию, совпадают.
Серединные перпендикуляры к сторонам треугольника пересекаются в одной
точке, которая совпадает с центром описанной окружности.