Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

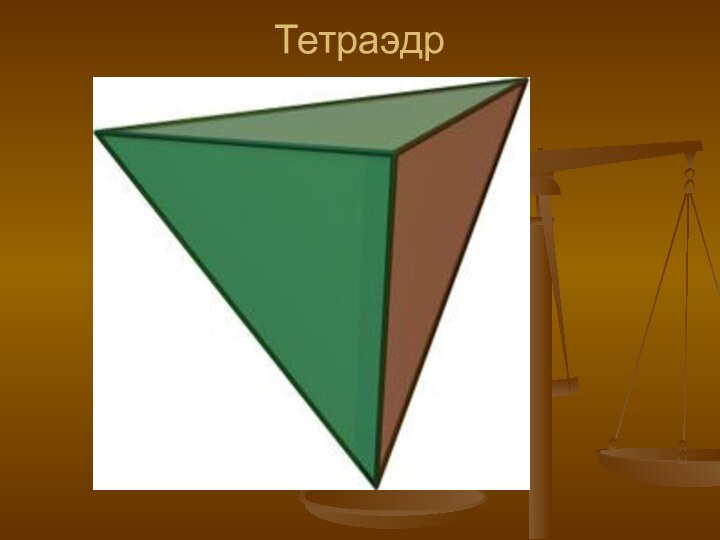
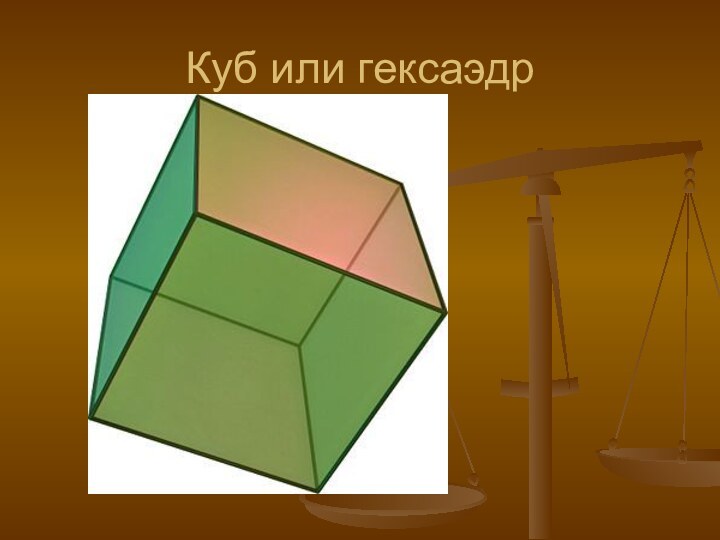
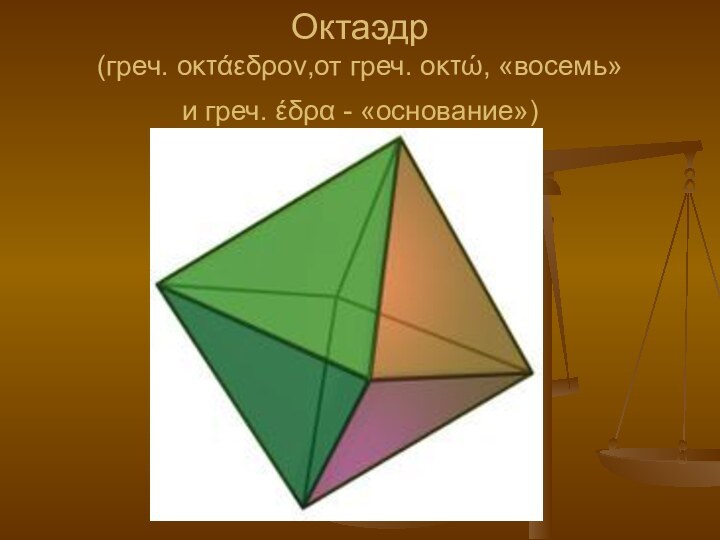
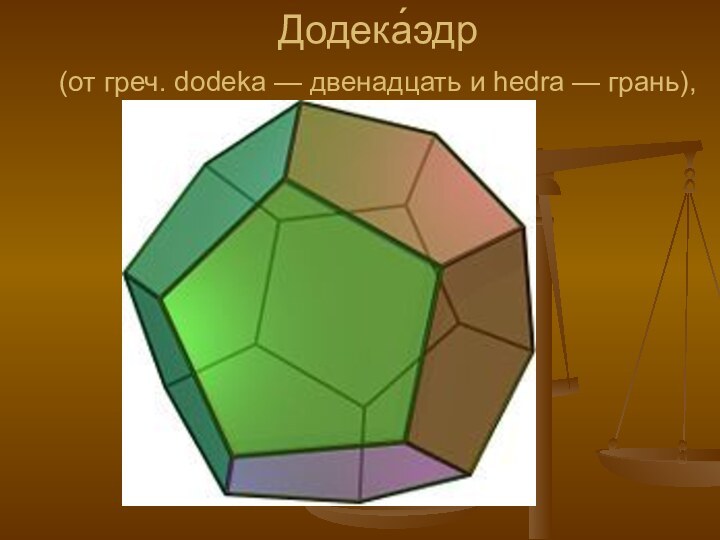
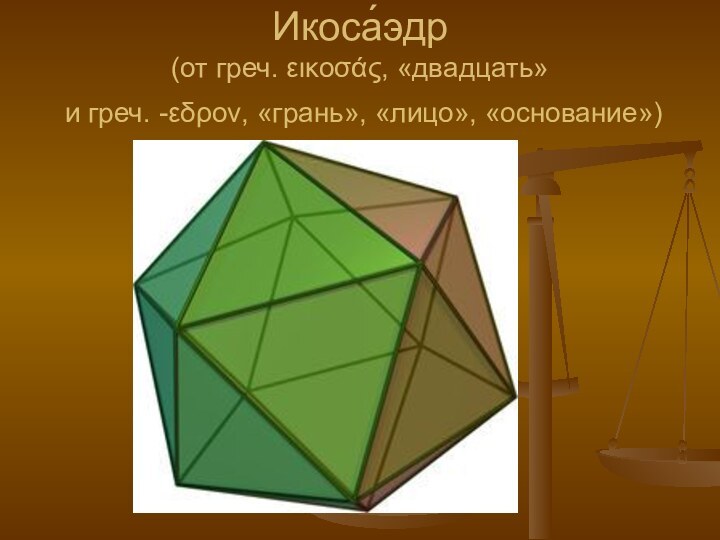
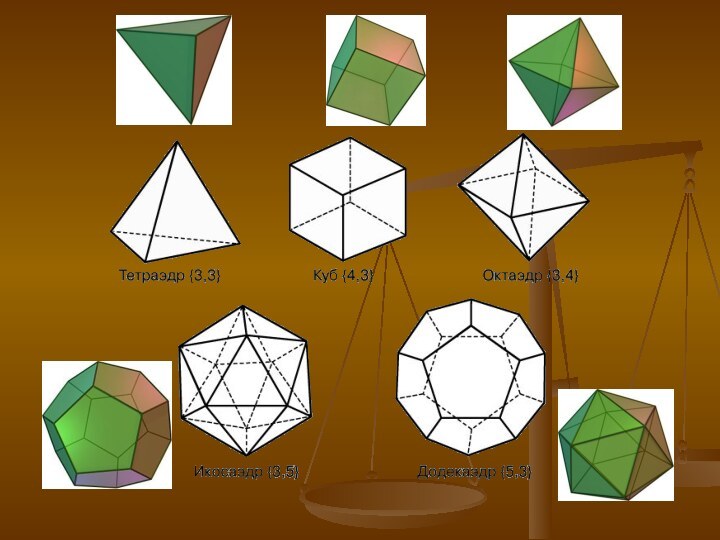
Презентация на тему Тела Платона

Содержание

Цель: Исследование - свойств платоновых тел - роли «Платоновых тел» в различных
Исследовательскаяработапо геометрии на тему:«Тела Платона». Цель: Исследование - ПЛАН.Введение.Определение.Свойства платоновых тел . Теорема Эйлера.Симметрия платоновых тел.Платоновы тела и биология.Платоновы тела При изучении теории правильных многогранников открывается не только удивительный Тетраэдр Куб или гексаэдр Октаэдр (греч. οκτάεδρον,от греч. οκτώ, «восемь» и греч. έδρα - «основание») Додека́эдр (от греч. dodeka — двенадцать и hedra — грань), Икоса́эдр (от греч. εικοσάς, «двадцать» и греч. -εδρον, «грань», «лицо», «основание») ТАБЛИЦА № 1. ТАБЛИЦА № 2. ТАБЛИЦА № 3. Теорема Эйлера Для любого Симметрия платоновых тел.ТетраэдрОктаэдр Додека́эдр Платоновы тела и биология. Формы вирусов Икоса́эдр Платоновы тела и химия куб передает форму кристаллов поваренной соли NaCl, Исследование земли Архимедовы тела.          Архимедовы тела.. . Конструирование Архимедовых тел (а) усеченный тетраэдр,(б) Правильные звездчатые многогранники Кеплер первым начал изучать так называемые звездчатые многогранники,которые в Платоновы тела и современность.Израильский физикДан ШехтманМ.Т. Крашек на своей выставке ‘Kaleidoscopic Fragrances’, Любляна, 2005 ЗАКЛЮЧЕНИЕ. Теория многогранников ( платоновых тел) - одна из увлекательных и Список использованной литературы. 1.Свечников А.А. «Путешествие в историю математики» г. Москва издательство
Слайды презентации

Слайд 2 Цель: Исследование

Цель: Исследование - свойств платоновых тел

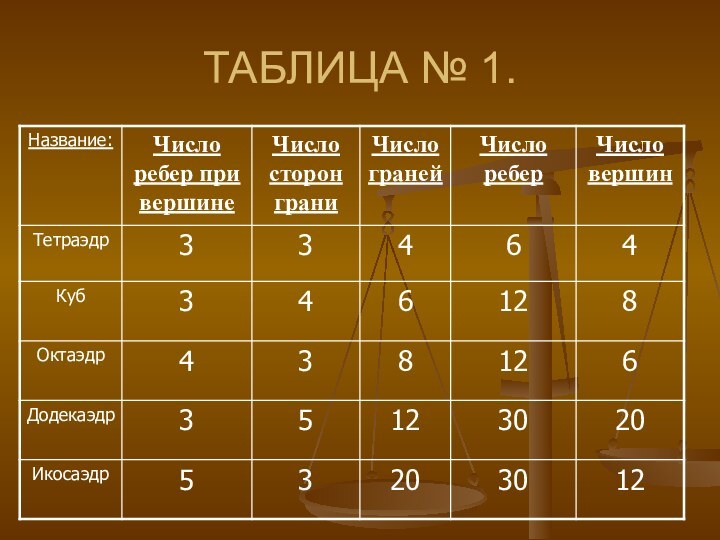
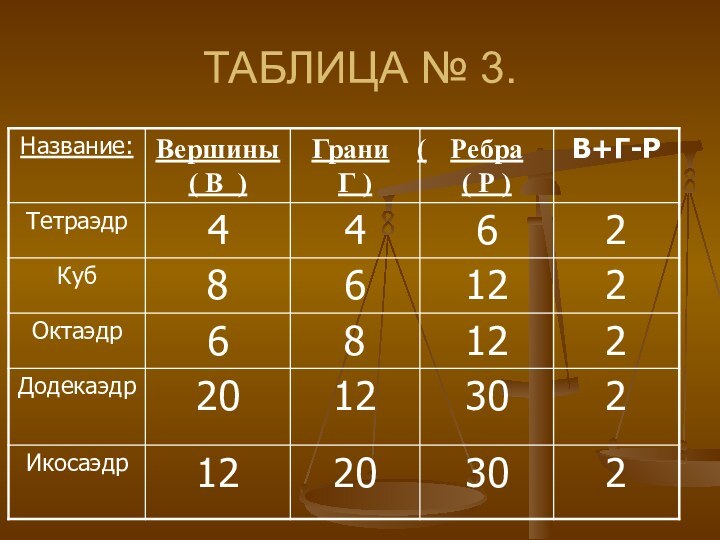
- свойств платоновых тел

- роли «Платоновых тел» в различных областях науки и живописи. Задачи:

Изучить
научную литературу,
ресурсы сети Интернет по исследуемой теме.
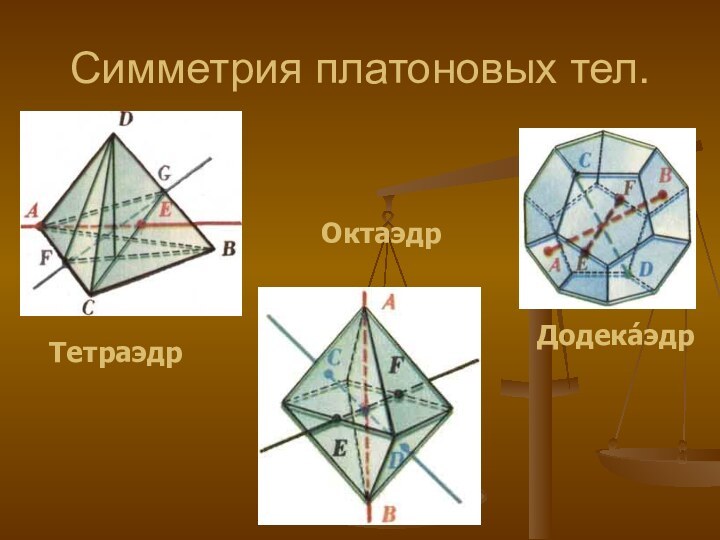
Выявить роль платоновых тел в
геометрии,
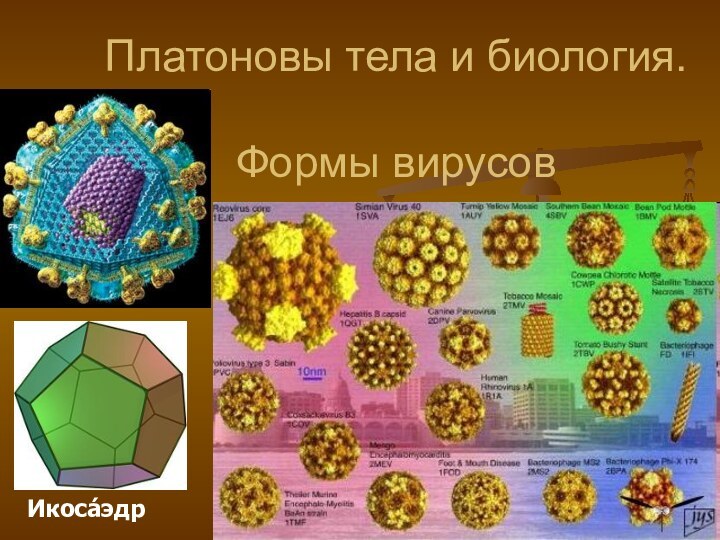
биологии,
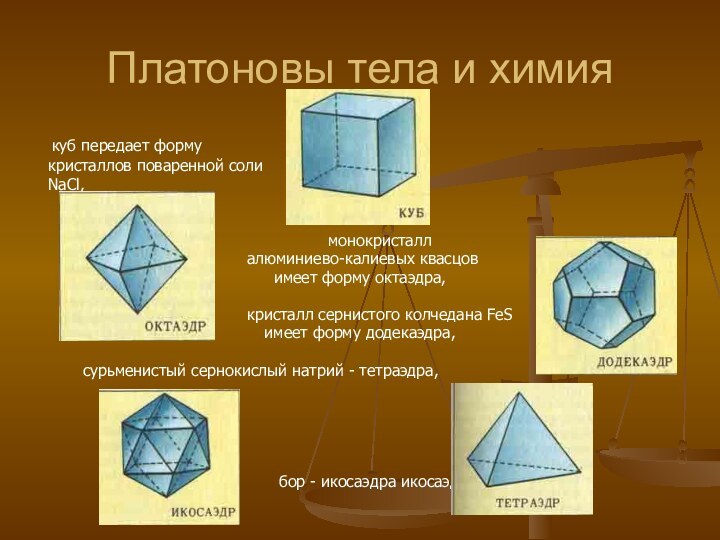
химии,
в исследовании земли.
Показать:
а) непосредственную связь платоновых тел и других наук.
б) прикладные возможности «платоновых тел».




Слайд 3 ПЛАН.
Введение.
Определение.
Свойства платоновых тел .
Теорема Эйлера.
Симметрия платоновых тел.
Платоновы

ПЛАН.Введение.Определение.Свойства платоновых тел . Теорема Эйлера.Симметрия платоновых тел.Платоновы тела и биология.Платоновы

тела и биология.
Платоновы тела и химия.
Исследование земли.
Архимедовы тела.
Правильные

звездчатые многогранники
Платоновы тела и современность.
Заключение.


Слайд 4
При изучении
теории правильных многогранников

При изучении теории правильных многогранников открывается не только удивительный мир

открывается не только удивительный мир геометрических тел,
обладающих неповторимыми

свойствами,
но и интересные
историко – философские концепции, оригинальные научные гипотезы.

Слайд 5 Тетраэдр

Тетраэдр

Слайд 6 Куб или гексаэдр

Куб или гексаэдр

Слайд 7 Октаэдр (греч. οκτάεδρον,от греч. οκτώ, «восемь» и греч. έδρα

Октаэдр (греч. οκτάεδρον,от греч. οκτώ, «восемь» и греч. έδρα - «основание»)

- «основание»)

Слайд 8 Додека́эдр (от греч. dodeka — двенадцать и hedra

Додека́эдр (от греч. dodeka — двенадцать и hedra — грань),

— грань),

Слайд 9 Икоса́эдр (от греч. εικοσάς, «двадцать» и греч. -εδρον,

Икоса́эдр (от греч. εικοσάς, «двадцать» и греч. -εδρον, «грань», «лицо», «основание»)

«грань», «лицо», «основание»)

Слайд 10

Слайд 11 ТАБЛИЦА № 1.

ТАБЛИЦА № 1.

Слайд 12 ТАБЛИЦА № 2.

ТАБЛИЦА № 2.

Слайд 13 ТАБЛИЦА № 3.

ТАБЛИЦА № 3.

Слайд 14

Теорема Эйлера Для любого выпуклого многогранника справедливо

Теорема Эйлера
Для любого выпуклого многогранника справедливо соотношение Г+В-Р=2,


где
Г – число граней,
В – число вершин ,
Р – число ребер
данного многогранника.

Слайд 15 Симметрия платоновых тел.
Тетраэдр
Октаэдр
Додека́эдр

Симметрия платоновых тел.ТетраэдрОктаэдр Додека́эдр

Слайд 16 Платоновы тела и биология. Формы вирусов
Икоса́эдр

Платоновы тела и биология. Формы вирусов Икоса́эдр

Слайд 17 Платоновы тела и химия
куб передает форму
кристаллов

Платоновы тела и химия куб передает форму кристаллов поваренной соли NaCl,

поваренной соли
NaCl,


монокристалл
алюминиево-калиевых

квасцов
имеет форму октаэдра,

кристалл сернистого колчедана FeS
имеет форму додекаэдра,

сурьменистый сернокислый натрий - тетраэдра,





бор - икосаэдра икосаэдра.

Слайд 18 Исследование земли

Исследование земли

Слайд 19

Архимедовы тела.          Архимедовыми

Архимедовы тела.
         

Архимедовыми телами называются
полуправильные ,
однородные выпуклые многогранники ,
то есть выпуклые многогранники ,
все  многогранные углы которых равны ,
а грани - правильные многогранники нескольких типов
(этим они отличаются от платоновых тел, грани которых - правильные многоугольники одного типа).

Слайд 20 Архимедовы тела.
.
. Конструирование
Архимедовых тел



Архимедовы тела.. . Конструирование Архимедовых тел (а) усеченный тетраэдр,(б)


(а)
усеченный
тетраэдр,
(б)
усеченный
куб,
(в)
усеченный

октаэдр,

г)
усеченный
додекаэдр,

(д)
усеченный
икосаэдр

(е)
кубооктаэдр,

(ж)
икосодо
декаэдр

(з)
ромбокубо
октаэдр,

(и) ромбоикосододекаэдр

(к)
курносый
куб

(л)
курносый
додекаэдр

(н)
Ромбоусеченй
икосододекаэдр

(м)
Ромбоусечеый
кубоктаэдр

Слайд 21 Правильные
звездчатые многогранники
Кеплер первым
начал изучать
так

Правильные звездчатые многогранники Кеплер первым начал изучать так называемые звездчатые многогранники,которые

называемые
звездчатые многогранники,
которые в отличие
от Платоновых и Архимедовых

тел
являются правильными
выпуклыми многогранниками.

Слайд 22 Платоновы тела и современность.
Израильский физик
Дан Шехтман
М.Т. Крашек на

Платоновы тела и современность.Израильский физикДан ШехтманМ.Т. Крашек на своей выставке ‘Kaleidoscopic Fragrances’, Любляна, 2005

своей выставке
‘Kaleidoscopic Fragrances’,
Любляна, 2005

Слайд 23

Слайд 24

Слайд 25 ЗАКЛЮЧЕНИЕ. Теория многогранников ( платоновых тел) - одна из

ЗАКЛЮЧЕНИЕ. Теория многогранников ( платоновых тел) - одна из увлекательных

увлекательных и ярких разделов математики.
В идеалистической картине

мира, данной великим мыслителем Платоном четыре из них олицетворяли четыре стихии:
Тетраэдр- огонь,
Куб- землю;
Икосаэдр- воду;
Октаэдр – воздух;

Додекаэдр –
символизировал все мироздание ,
по латыни его стали называть
«пятая сущность»

  • Имя файла: tela-platona.pptx
  • Количество просмотров: 193
  • Количество скачиваний: 2
- Предыдущая Весёлое путешествие в Страну Знаний
Следующая - Государственная символика России Герб

Похожие презентации

Решение задач на применение аксиом стереометрии и их следствий Решение задач на применение аксиом стереометрии и их следствий 182
Презентация по геометрии Объемы многогранников и тел вращения Презентация по геометрии Объемы многогранников и тел вращения 154
Презентация по геометрии на тему Аксиомы планиметрии Презентация по геометрии на тему Аксиомы планиметрии 165
Графические приемы. Координатная плоскость Графические приемы. Координатная плоскость 154
Параллельные прямые в пространстве Параллельные прямые в пространстве 181
Презентация по математике Повторение по теме Четырехугольники (9 класс) Презентация по математике Повторение по теме Четырехугольники (9 класс) 167
Соотношение между сторонами и углами треугольника Соотношение между сторонами и углами треугольника 155
Из чего строится геометрия Из чего строится геометрия 157
Презентация по геометрии на тему Векторы Презентация по геометрии на тему Векторы 139
Соотношения между сторонами и углами в треугольнике Соотношения между сторонами и углами в треугольнике 163
Площадь. Формула площади прямоугольника Площадь. Формула площади прямоугольника 175
Задачи на построение Задачи на построение 309
Основные геометрические фигуры Основные геометрические фигуры 162
Презентация по геометрии Свойства параллельных прямых Презентация по геометрии Свойства параллельных прямых 158
Презентация проекта по геометрии на тему Лист Мёбиуса(9 класс) Презентация проекта по геометрии на тему Лист Мёбиуса(9 класс) 240
Все о целиндре Все о целиндре 200
Три признака равенства треугольников Три признака равенства треугольников 133
Презентация по геометрии на тему Подобные треугольники Презентация по геометрии на тему Подобные треугольники 159
Построение треугольника по трем элементам Построение треугольника по трем элементам 154
Метод золотого сечения Метод золотого сечения 163
Практическая геометрия у разных народов мира Практическая геометрия у разных народов мира 169
Нанесение размеров. Масштабы Нанесение размеров. Масштабы 161
Презентация к уроку геометрии на тему Построение треугольников (8 класс) Презентация к уроку геометрии на тему Построение треугольников (8 класс) 161
Презентация по геометрии на тему Площадь треугольника (8 класс) Презентация по геометрии на тему Площадь треугольника (8 класс) 174
Презентация по геометрии на тему Площадь круга (9 класс) Презентация по геометрии на тему Площадь круга (9 класс) 156
Презентация к уроку геометрии в 8 классе по теме Четырёхугольники Презентация к уроку геометрии в 8 классе по теме Четырёхугольники 142
Урок математики в 11 классе по теме Двугранный угол. Трехгранный и многогранный углы Урок математики в 11 классе по теме Двугранный угол. Трехгранный и многогранный углы 210
Диктант по геометрии Площадь треугольника Диктант по геометрии Площадь треугольника 173
Параллельность плоскостей в пространстве Параллельность плоскостей в пространстве 182
Теорема Пифагора Теорема Пифагора 223