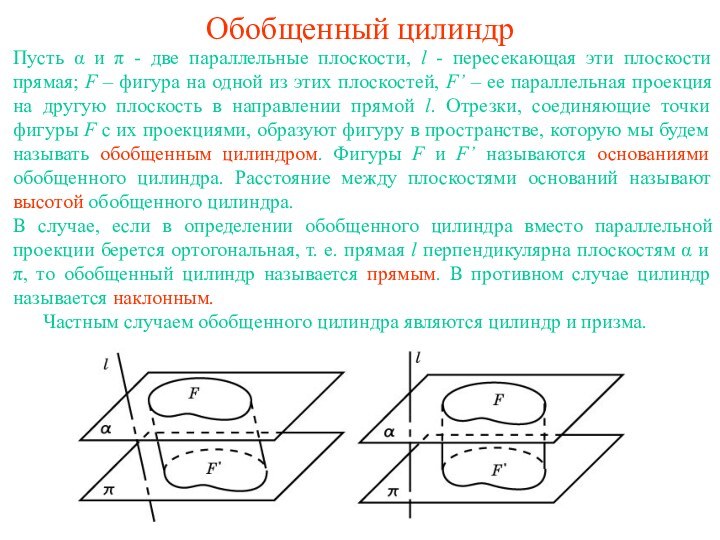
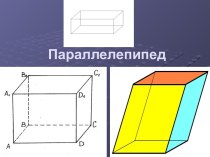
плоскости, l - пересекающая эти плоскости прямая; F –
фигура на одной из этих плоскостей, F’ – ее параллельная проекция на другую плоскость в направлении прямой l. Отрезки, соединяющие точки фигуры F с их проекциями, образуют фигуру в пространстве, которую мы будем называть обобщенным цилиндром. Фигуры F и F’ называются основаниями обобщенного цилиндра. Расстояние между плоскостями оснований называют высотой обобщенного цилиндра.В случае, если в определении обобщенного цилиндра вместо параллельной проекции берется ортогональная, т. е. прямая l перпендикулярна плоскостям α и π, то обобщенный цилиндр называется прямым. В противном случае цилиндр называется наклонным.
Частным случаем обобщенного цилиндра являются цилиндр и призма.