- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Призма
Содержание
- 2. Цели урока:Вспомнить понятие призмы.Изучить теорему об объеме призмы.Провести доказательство.Применить полученные знания на практике.
- 3. Призма – многогранник, составленный из двух равных
- 4. Если боковые ребра призмы перпендикулярны к основаниям,
- 5. Теорема: Объем прямой призмы равен произведению площади
- 6. Рассмотрим прямую треугольную призму ABCA1B1C1 с объёмом
- 7. Теорема для произвольной прямой призмы с высотой
- 8. ЗадачаДано: ABCA1B1C1- прямая призма.AB=BC=m; ABC= φ,BD- высота в ∆ ABC;BB1=BD.Найти: VABCA1B1C1-?
- 9. Решение:S ABC ·h, h=BB1.Рассмотрим ∆ ABC; ∆
- 10. Вопросы:Как найти объем прямой призмы?Основные шаги при доказательстве теоремы прямой призмы?
- 11. Работу выполнили: Шахбазян Эллена,11”В” Шмырева Юлия,11 “В” Двадненко Аня,11 “В”
- 12. Скачать презентацию
- 13. Похожие презентации
Цели урока:Вспомнить понятие призмы.Изучить теорему об объеме призмы.Провести доказательство.Применить полученные знания на практике.








Слайд 2
Цели урока:
Вспомнить понятие призмы.
Изучить теорему об объеме призмы.
Провести
доказательство.
Слайд 3 Призма – многогранник, составленный из двух равных многоугольников
A1A2…An и B1B2 и Bn, расположенных в параллельных плоскостях,
и n параллелограммов.Слайд 4 Если боковые ребра призмы перпендикулярны к основаниям, то
призма называется прямой.
Прямая призма называется правильной, если её основания
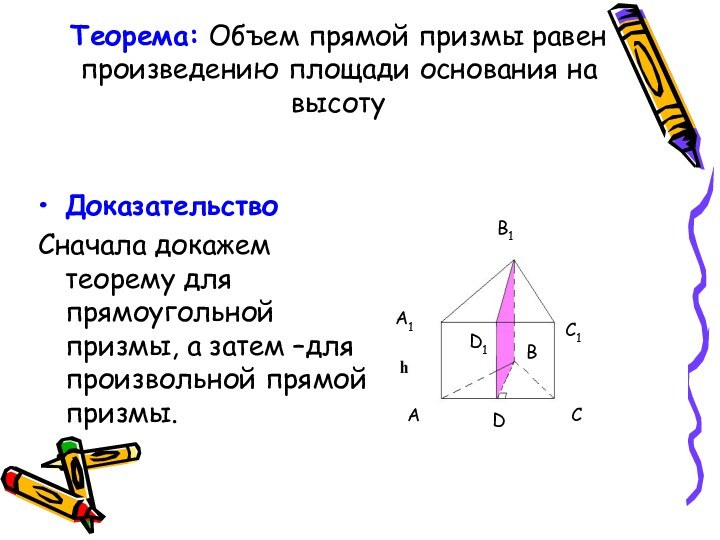
– правильные многоугольники. Слайд 5 Теорема: Объем прямой призмы равен произведению площади основания
на высоту
Доказательство
Сначала докажем теорему для прямоугольной призмы, а затем
–для произвольной прямой призмы.В
D1
А1
В1
С1
А
C
D
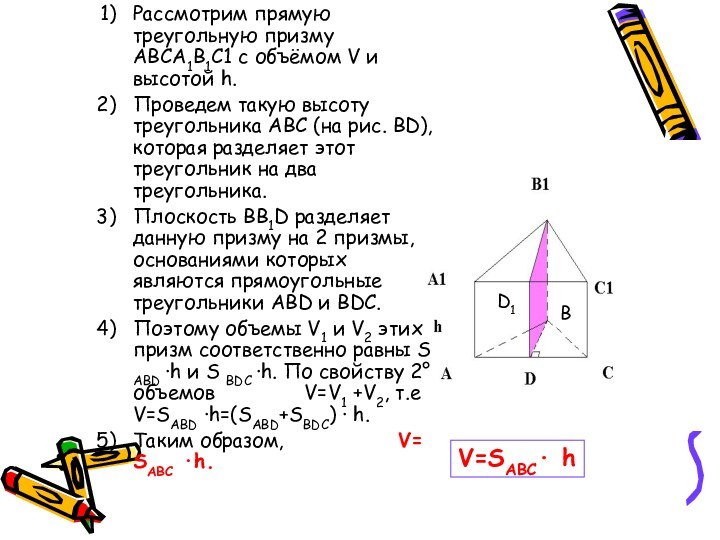
Слайд 6 Рассмотрим прямую треугольную призму ABCA1B1C1 с объёмом V
и высотой h.
Проведем такую высоту треугольника ABC (на рис.
BD),которая разделяет этот треугольник на два треугольника.Плоскость BB1D разделяет данную призму на 2 призмы, основаниями которых являются прямоугольные треугольники ABD и BDC.
Поэтому объемы V1 и V2 этих призм соответственно равны S ABD ·h и S BDC ·h. По свойству 2° объемов V=V1 +V2, т.е V=SABD ·h=(SABD+SBDC) · h.
Таким образом, V= SABC ·h.
V=SABC∙ h
В
D1
Слайд 7 Теорема для произвольной прямой призмы с высотой h
и площадью основания S.
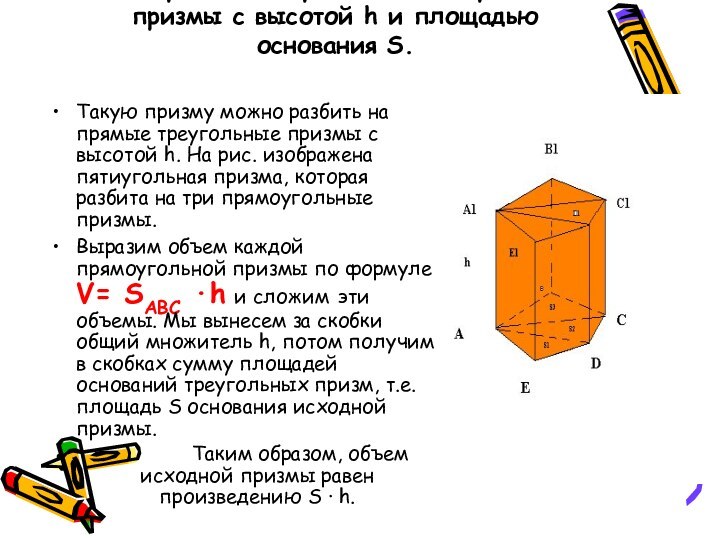
Такую призму можно разбить на прямые
треугольные призмы с высотой h. На рис. изображена пятиугольная призма, которая разбита на три прямоугольные призмы. Выразим объем каждой прямоугольной призмы по формуле V= SABC ·h и сложим эти объемы. Мы вынесем за скобки общий множитель h, потом получим в скобках сумму площадей оснований треугольных призм, т.е. площадь S основания исходной призмы.
Таким образом, объем исходной призмы равен произведению S · h.
Слайд 8
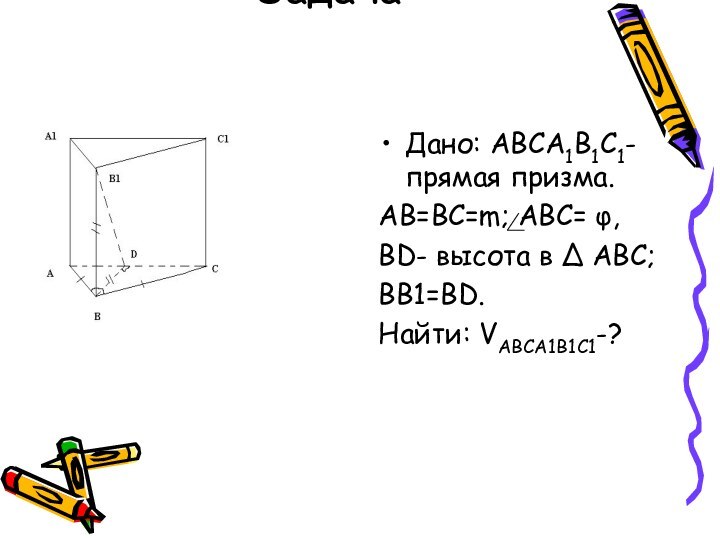
Задача
Дано: ABCA1B1C1- прямая призма.
AB=BC=m; ABC= φ,
BD- высота в
∆ ABC;
BB1=BD.
Найти: VABCA1B1C1-?
Слайд 9
Решение:
S ABC ·h, h=BB1.
Рассмотрим ∆ ABC; ∆ ABC-
р/б. BD- высота ∆ ABC, следовательно медиана и
биссектриса.ABD= DBC= φ/2
3) Рассмотрим ∆ ABD; ∆ ABD- прямоугольный. Из соотношения в ∆: cosφ/2 = BD/AB BD= cosφ/2 AB, BD=m cosφ/2 (AB=m)
4) Т.к. BD=BB1 BB1=m · cos φ /2
5) S ABC= ½ AB·BC· sinφ; S ABC= ½ m2 · sinφ
6) V= ½ m2 · sinφ· mcosφ/2=½ m3 · sinφ · cosφ/2
Ответ: ½ m3 · sinφ · cosφ/2