Презентация на тему Подобные треугольники

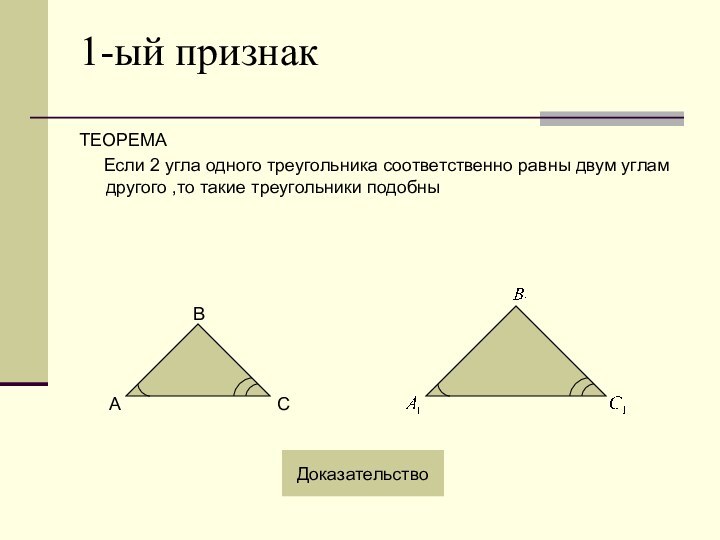
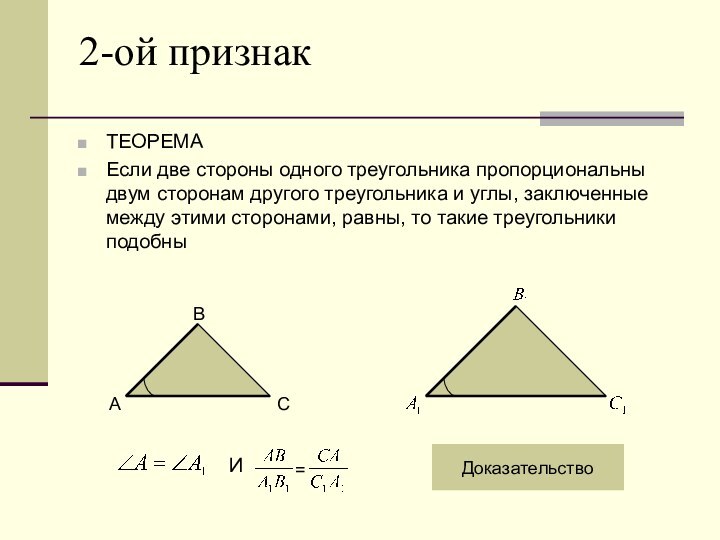
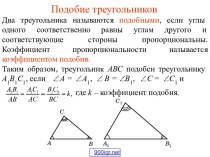
длин, т.е.
Говорят, что отрезки AB и CD пропорциональны отрезкам

и , если = .

Например, отрезки AB и CD, длины которых равны 2см и 1см, пропорциональны отрезкам и , длины которых равны 3см и 1,5см. В самом деле, = = .

Понятие пропорциональности вводится и для большего числа отрезков. Так, например 3 отрезка АВ, CD и EF пропорциональны трем отрезкам , и , если справедливо равенство , = = .

Пропорциональные отрезки

углы соответственно равны:

, , . В этом случае стороны АВ и , ВC и , CA и называются сходственными.

Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.

Другими словами 2 треугольника называются подобными если:

1)

2) , где k коэффициент подобия

квадрату коэффициента подобия


А
В
С

треугольника соответственно равны двум углам другого ,то такие треугольники

подобны

А

В

С

Доказательство

сторонам другого треугольника и углы, заключенные между этими сторонами,

равны, то такие треугольники подобны

А

В

С

И

=

Доказательство

другого, то такие треугольники подобны


А
В
С

Доказательство

.
Т.к.
и
то

и
=
Аналогично для
и
Получим
=

у которого
1
2
и
Треугольники

и

подобны по первому признаку

и

=

Треугольники АВС и

равны (СУС)

и

признаку
и
Треугольник АВС=
(3 стороны)

Т.к.
и

Учитывая второй признак подобия можно

доказать что

АВС подобен