Презентация на тему Подготовка к ГИА по математике Все о четырехугольниках

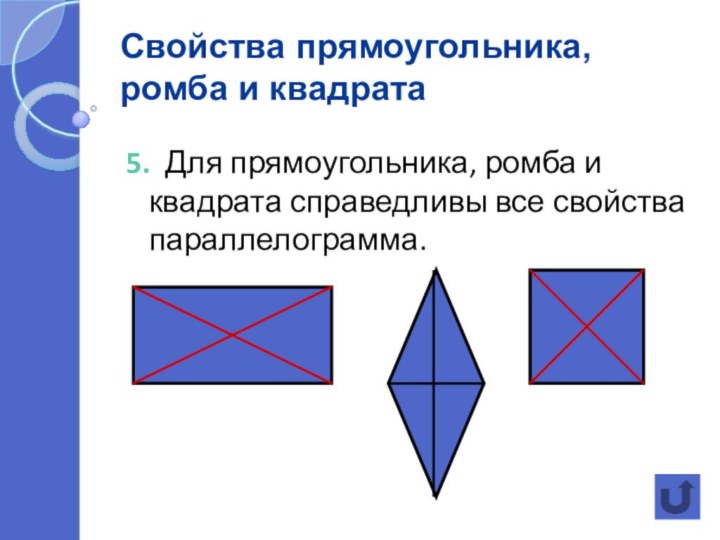
а) Свойства прямоугольника, ромба, квадрата
Трапеция (определения,

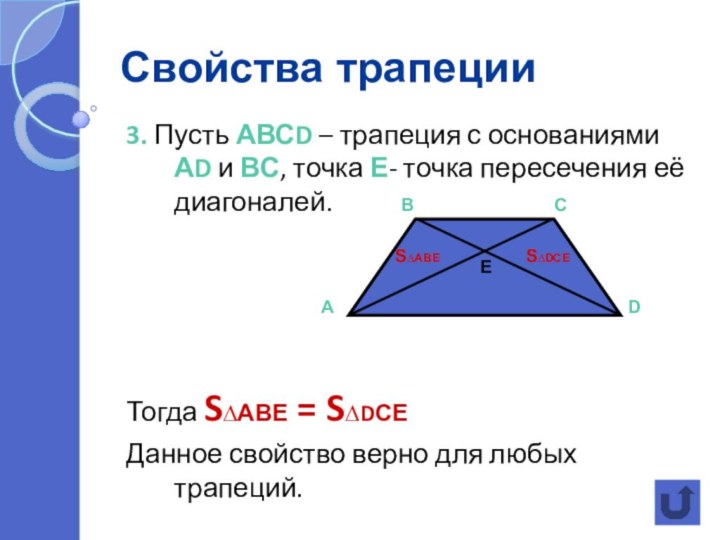
виды)
а) Свойства трапеции
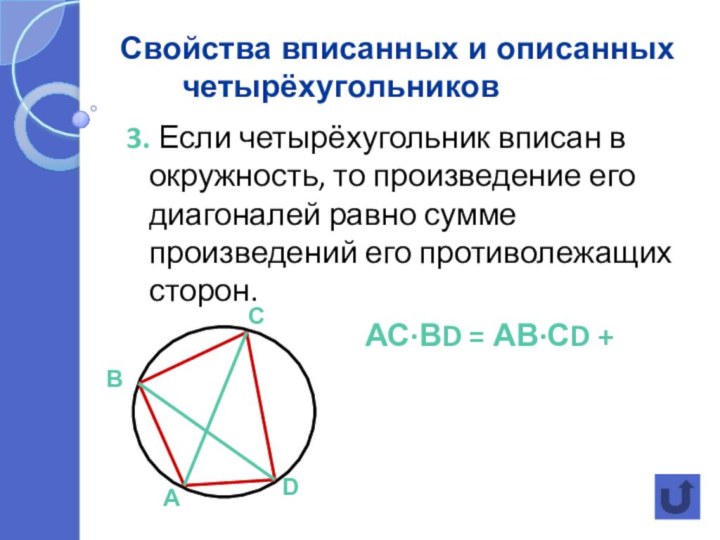
Свойства вписанных и описанных четырёхугольников
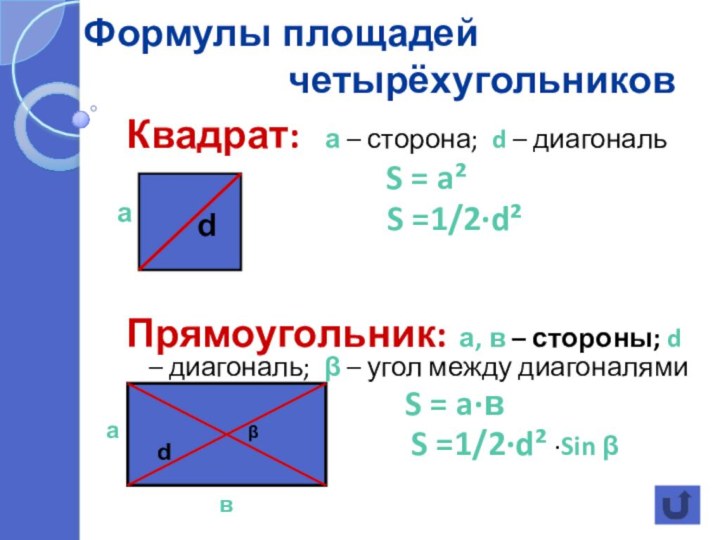
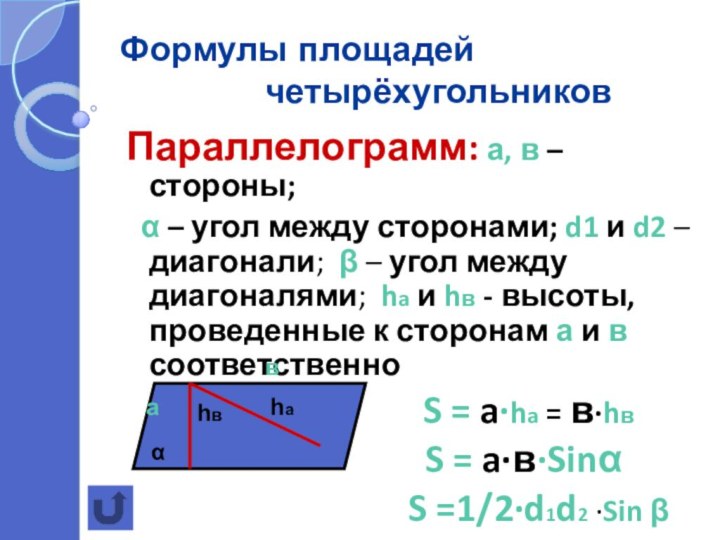
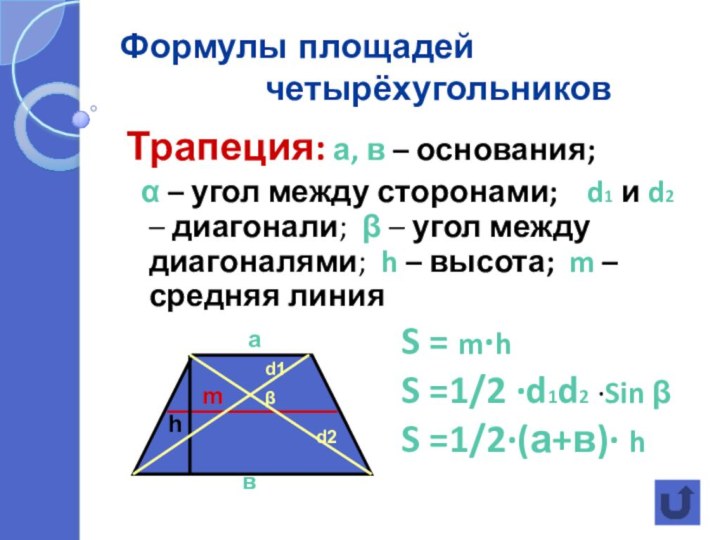
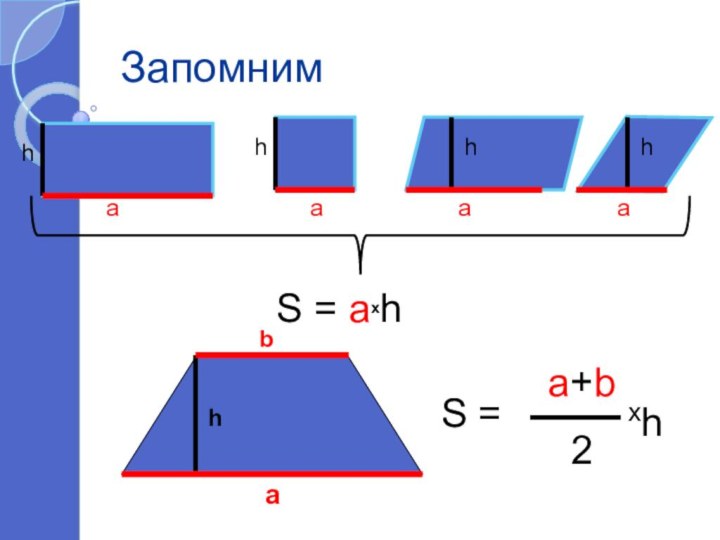
Формулы площадей
а) прямоугольника и квадрата
б) параллелограмма
в) ромба
г) трапеции
д) произвольного четырёхугольника

четырьмя сторонами
Соседние вершины – вершины, являющиеся концами одной из

сторон четырёхугольника
Противолежащие вершины – вершины не являющиеся соседними
Диагонали четырёхугольника – отрезки, соединяющие противолежащие вершины.
Соседние стороны – стороны, исходящие из одной вершины.
Противолежащие стороны – стороны, не являющиеся соседними.
Периметр – сумма длин всех сторон четырёхугольника.

параллельны

параллелограмма равны
3. Диагонали параллелограмма пересекаются и точкой пересечения делятся

пополам

Утверждения, обратные свойствам 1-3, являются признаками параллелограмма, т.е.
если противолежащие стороны четырёхугольника равны, то этот четырёхугольник - параллелограмм

удвоенной сумме квадратов его сторон.

т.е.

d1

d2

а

в

все углы прямые
Ромб – это параллелограмм, у которого все

стороны равны.
Квадрат – это прямоугольник, у которого все стороны равны.
Квадрат – это ромб, у которого все углы прямые.

Диагонали ромба пересекаются под прямым углом.
3. Диагонали ромба являются

биссектрисами его углов.
4. Диагонали квадрата:
1) равны
2) пересекаются под прямым углом
3) являются биссектрисами его углов

и квадрата справедливы все свойства параллелограмма.

стороны параллельны, а две другие стороны не параллельны.
Основания трапеции

– её параллельные стороны.
Боковые стороны трапеции – непараллельные, противолежащие стороны трапеции
Высота трапеции – это отрезок перпендикуляра от любой точки одного основания до её другого основания(или его продолжения)
Средняя линия трапеции – отрезок соединяющий середины боковых сторон трапеции.

и равна их полусумме.

2. У равнобокой трапеции углы при

основании (верхнем и нижнем) равны.

АD и ВС, точка Е- точка пересечения её диагоналей.

Тогда S∆АВЕ = S∆DСЕ
Данное свойство верно для любых трапеций.

А

В

С

D

Е

S∆АВЕ

S∆DСЕ

четырёхугольников
1. Четырёхугольник можно вписать в окружность тогда и только

тогда, когда сумма его противолежащих углов равна 180°
А + С = В + D = 180°

А

В

С

D

четырёхугольников
2. Четырёхугольник можно описать около окружности тогда и только

тогда, когда суммы его противолежащих сторон равны.

а + с = в + d

а

в

с

d

четырёхугольников
3. Если четырёхугольник вписан в окружность, то произведение его

диагоналей равно сумме произведений его противолежащих сторон.
АС·ВD = АВ·СD + АD·ВС

А

В

С

D

четырёхугольников
Квадрат: а – сторона;

d – диагональ
S = a²
S =1/2·d²


Прямоугольник: а, в – стороны; d – диагональ; β – угол между диагоналями
S = a·в
S =1/2·d² ·Sin β

а

d

а

в

β

d

четырёхугольников

Параллелограмм: а, в – стороны;
α – угол между сторонами; d1 и d2 – диагонали; β – угол между диагоналями; ha и hв - высоты, проведенные к сторонам а и в соответственно
S = a·ha = в·hв
S = a·в·Sinα
S =1/2·d1d2 ·Sin β

а

в

α

ha

hв

четырёхугольников

Ромб: а – сторона; α – угол между сторонами; d1 и d2 – диагонали; h – высота
S = a·h
S = a²·Sinα
S =1/2·d1d2

а

d1

d2

h

четырёхугольников

Трапеция: а, в – основания;
α – угол между сторонами; d1 и d2 – диагонали; β – угол между диагоналями; h – высота; m – средняя линия
S = m·h
S =1/2 ·d1d2 ·Sin β
S =1/2·(а+в)· h

в

а

h

m

d1

d2

β

четырёхугольников

Произвольный четырёхугольник: d1 и d2 – диагонали; β – угол между диагоналями

S =1/2 ·d1d2 ·Sin β

d1

d2

β