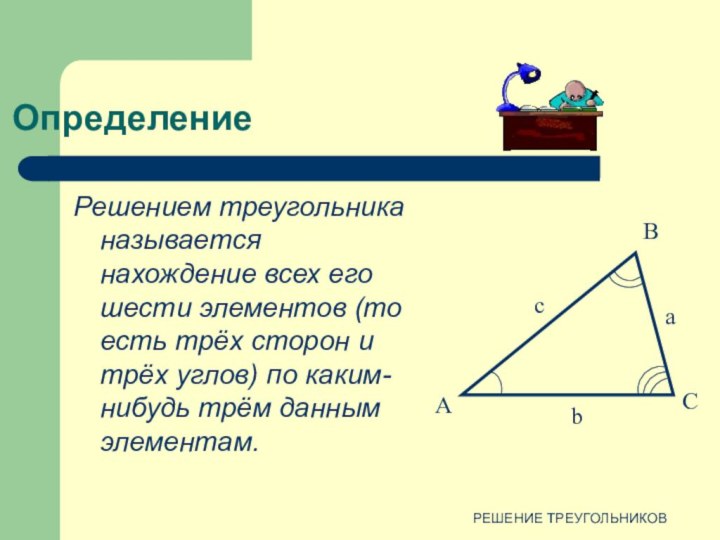
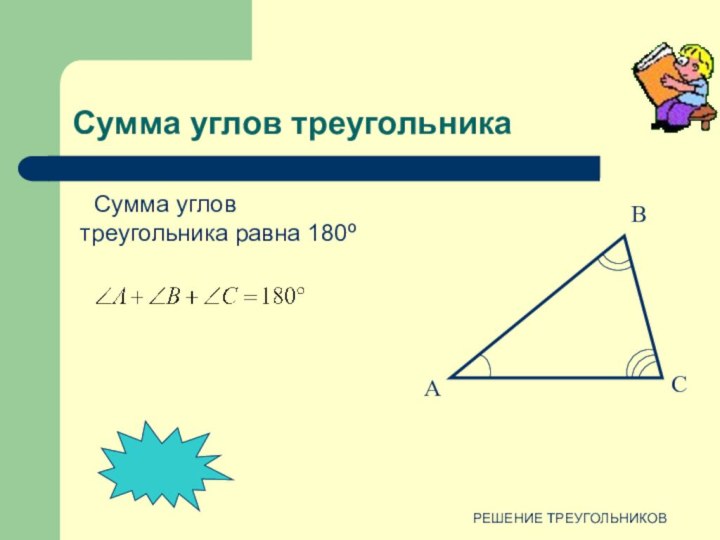
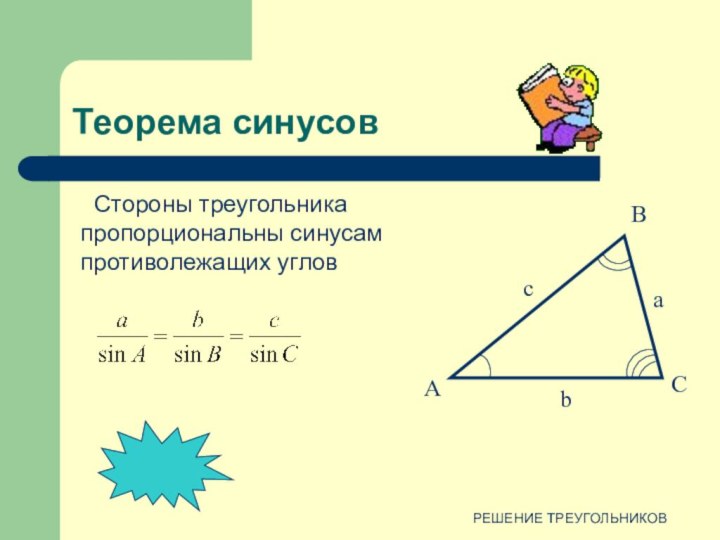
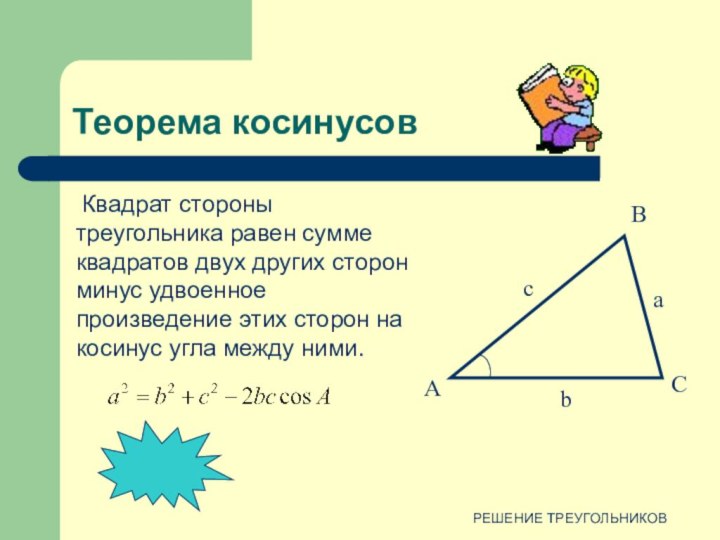
против угла в 150º лежит большая сторона.
В равностороннем треугольнике
внутренние углы равны между собой и каждый равен 60º.Существует треугольник со сторонами 2 см, 7 см, 3 см.
Прямоугольный равнобедренный треугольник имеет равные катеты.
Сумма длин двух других сторон любого треугольника меньше третьей стороны.
Если острый угол прямоугольного треугольника равен 60º, то прилежащий к нему катет равен половине гипотенузы.
Существует треугольник с двумя тупыми углами.
В прямоугольном треугольнике сумма острых углов равна 90º.