и
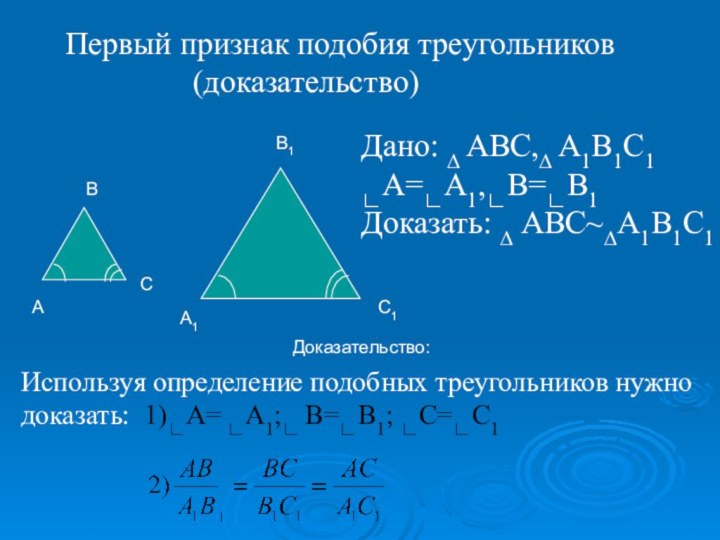
стороны одного треугольника
пропорциональны сходственным
сторонам другого, т.е.
А
В
С
А1
В1
С1
А
нельзя ли проще проверить, являются ли треугольники подобными?