Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Решение задач на теорему Пифагора

Содержание

Цель урока: рассмотреть теорему Пифагора и показать ее применение в ходе решения задач и на практике
Урок-презентация на тему ТЕОРЕМА ПИФАГОРАГЕОМЕТРИЯ 8 КЛАСС Цель урока: рассмотреть теорему Пифагора и показать ее применение в ходе решения задач и на практике Ход урокаI. Организационный моментII. 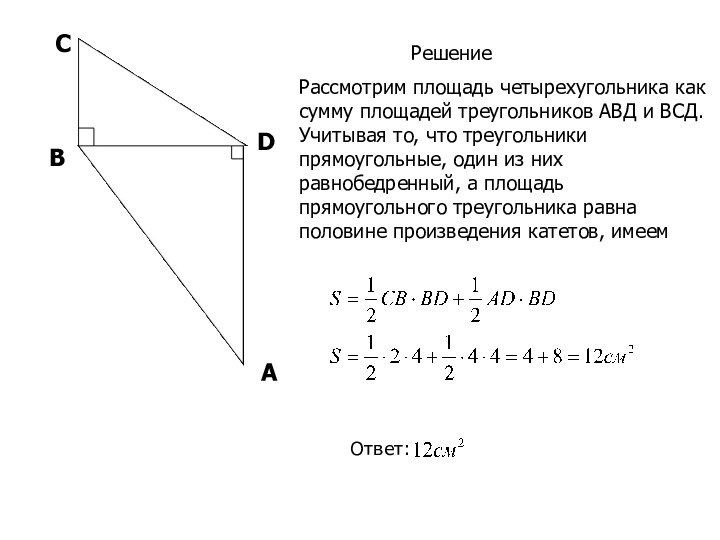Актуализация знаний учащихсяНесколько слов о прямоугольных треугольникахРешение задач ДАТЬ ОПРЕДЕЛЕНИЕ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКАОПРЕДЕЛЕНИЕ КАТЕТОВ И ГИПОТЕНУЗЫПРИЗНАКИ РАВЕНСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВФОРМУЛА НАХОЖДЕНИЯ ПЛОЩАДИ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКАПРЯМОУГОЛЬНЫЕ ТРЕУГОЛЬНИКИ Дано: АВСД – четырехугольник, AD = 4 см, СВ = 2 см--------------------------------------- Найти РешениеРассмотрим площадь четырехугольника III.Изучение нового материалаТеорема ПифагораВ прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов Доказательство Достроим треугольник до квадрата со стороной a+bПлощадь квадрата можно найти по формулеabbacaabbcccС Таким образом имеемТеорема доказана 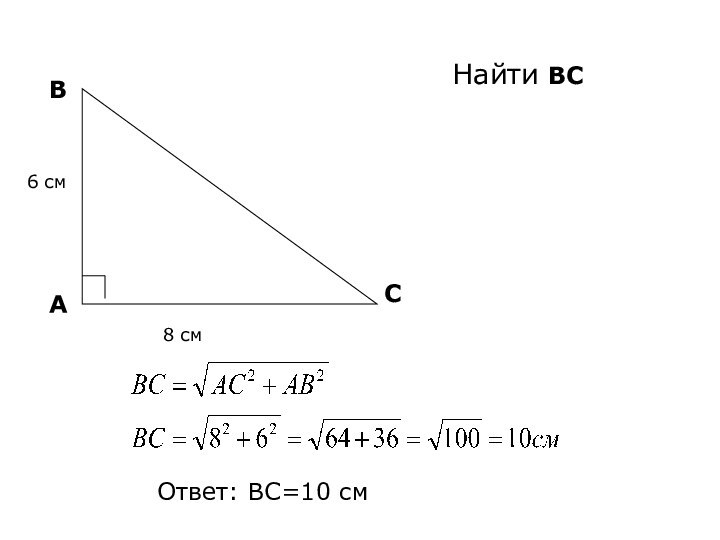АВС6 см8 смНайти ВСОтвет: ВС=10 см 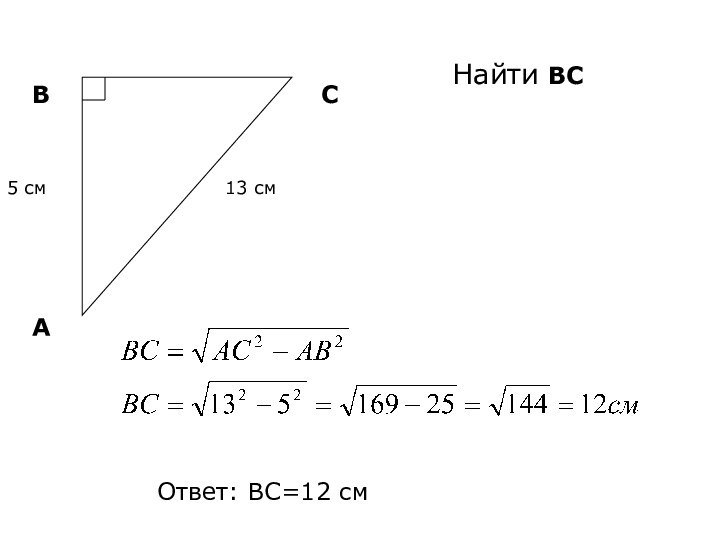АВС5 см13 смНайти ВСОтвет: ВС=12 см АСВ4 см5 смDНайти AСТак как треугольник АВС равнобедренный,То ВС – высота и Дополнительные задачиОснования равнобедренной трапеции равны 20 см и 30 см, боковые стороны 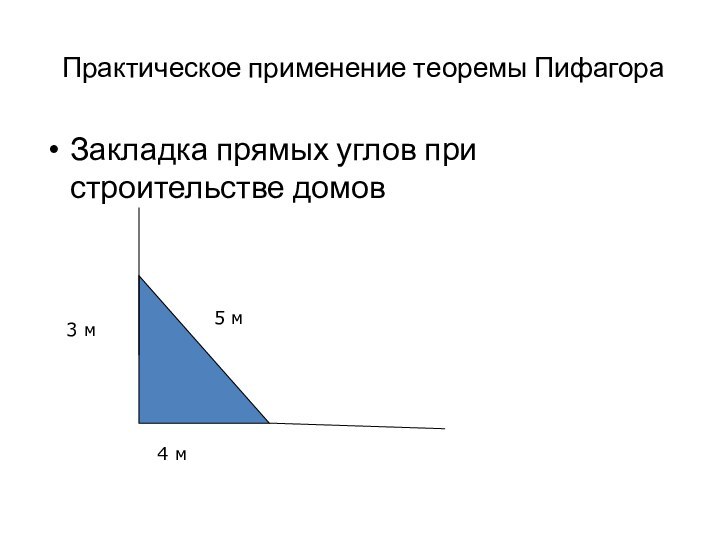Практическое применение теоремы ПифагораЗакладка прямых углов при строительстве домов3 м4 м5 м Домашнее заданиеП.54, вопрос 8, №483(устно), №485, №487.
Слайды презентации

Слайд 2 Цель урока: рассмотреть теорему Пифагора и показать ее

Цель урока: рассмотреть теорему Пифагора и показать ее применение в ходе решения задач и на практике

применение в ходе решения задач и на практике

Слайд 3 Ход урока
I. Организационный момент
II. Актуализация знаний учащихся
Несколько слов

Ход урокаI. Организационный моментII. Актуализация знаний учащихсяНесколько слов о прямоугольных треугольникахРешение

о прямоугольных треугольниках
Решение задач по готовым чертежам с целью

подготовки учащихся к восприятию нового материала

Слайд 4 ДАТЬ ОПРЕДЕЛЕНИЕ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА
ОПРЕДЕЛЕНИЕ КАТЕТОВ И ГИПОТЕНУЗЫ
ПРИЗНАКИ РАВЕНСТВА

ДАТЬ ОПРЕДЕЛЕНИЕ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКАОПРЕДЕЛЕНИЕ КАТЕТОВ И ГИПОТЕНУЗЫПРИЗНАКИ РАВЕНСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВФОРМУЛА НАХОЖДЕНИЯ ПЛОЩАДИ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКАПРЯМОУГОЛЬНЫЕ ТРЕУГОЛЬНИКИ

ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ
ФОРМУЛА НАХОЖДЕНИЯ ПЛОЩАДИ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА
ПРЯМОУГОЛЬНЫЕ ТРЕУГОЛЬНИКИ

Слайд 5





Дано: АВСД – четырехугольник,
AD = 4 см,

Дано: АВСД – четырехугольник, AD = 4 см, СВ = 2 см--------------------------------------- Найти

СВ = 2 см


---------------------------------------
Найти



Слайд 6

РешениеРассмотрим площадь четырехугольника как сумму площадей

Решение
Рассмотрим площадь четырехугольника как сумму площадей треугольников АВД

и ВСД. Учитывая то, что треугольники прямоугольные, один из них равнобедренный, а площадь прямоугольного треугольника равна половине произведения катетов, имеем


Ответ:


Слайд 7 III.Изучение нового материала
Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы

III.Изучение нового материалаТеорема ПифагораВ прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

равен сумме квадратов катетов

Слайд 8
Доказательство

Доказательство

Слайд 9 Достроим треугольник до квадрата со стороной a+b
Площадь квадрата

Достроим треугольник до квадрата со стороной a+bПлощадь квадрата можно найти по

можно найти по формуле
a
b


b
a
c



a
a
b
b
c
c
c

С другой стороны, этот квадрат составлен

из четырех равных (по двум катетам) прямоугольных треугольников, площадь каждого из них


и квадрата со стороной с и площадью


Слайд 10 Таким образом имеем



Теорема доказана

Таким образом имеемТеорема доказана

Слайд 11
А
В
С
6 см
8 см
Найти ВС

Ответ: ВС=10 см

АВС6 см8 смНайти ВСОтвет: ВС=10 см

Слайд 12
А
В
С
5 см
13 см
Найти ВС

Ответ: ВС=12 см

АВС5 см13 смНайти ВСОтвет: ВС=12 см

Слайд 13


А
С
В


4 см
5 см
D
Найти AС


Так как треугольник АВС равнобедренный,
То

АСВ4 см5 смDНайти AСТак как треугольник АВС равнобедренный,То ВС – высота

ВС – высота и медиана, а значит
АС=2DC, АС=6

см

Ответ: АС=6 см

Слайд 14 Дополнительные задачи
Основания равнобедренной трапеции равны 20 см и

Дополнительные задачиОснования равнобедренной трапеции равны 20 см и 30 см, боковые

30 см, боковые стороны – 13 см. Найти площадь

трапеции.
Сторона квадрата равна а см. Найти длину диагонали.
Диагонали ромба равны 14 см и 48 см. Найдите сторону ромба.

Слайд 15 Практическое применение теоремы Пифагора
Закладка прямых углов при

Практическое применение теоремы ПифагораЗакладка прямых углов при строительстве домов3 м4 м5 м

строительстве домов


3 м
4 м
5 м

  • Имя файла: reshenie-zadach-na-teoremu-pifagora.pptx
  • Количество просмотров: 179
  • Количество скачиваний: 0
- Предыдущая Сложение и вычитание многозначных чисел (3 класс)
Следующая - Чёрный ящик.Презентация Microsoft Office PowerPoint.ЧЕрный ящик.игра

Похожие презентации

Теорема о сумме углов треугольника Теорема о сумме углов треугольника 153
Движения Движения 136
Объем цилиндра Объем цилиндра 144
Задачи на подобие Задачи на подобие 136
Презентация для 9 класса по теме Решение задач по теме Векторы Презентация для 9 класса по теме Решение задач по теме Векторы 170
Прямоугольный параллелепипед. Куб. Площадь поверхности Прямоугольный параллелепипед. Куб. Площадь поверхности 170
Объём пирамиды Объём пирамиды 219
Треугольник. Вписанная окружность Треугольник. Вписанная окружность 318
Презентация по геометрии Своя игра Туманность конуса Презентация по геометрии Своя игра Туманность конуса 166
Нахождение площади параллелограмма Нахождение площади параллелограмма 198
Внешний угол треугольника 7 класс Внешний угол треугольника 7 класс 199
Периметр и площадь Периметр и площадь 224
Правильные многогранники 10 класс Правильные многогранники 10 класс 240
Площадь круга 6 класс Площадь круга 6 класс 175
Признаки параллельности прямых Признаки параллельности прямых 144
Презентация Урок - экскурсия по Дубаю ( интегрированный урок : геометрия + история). Тема урока: Объемы тел Презентация Урок - экскурсия по Дубаю ( интегрированный урок : геометрия + история). Тема урока: Объемы тел 159
аксонометрия аксонометрия 174
Презентация по геометрии по материалам ОГЭ Презентация по геометрии по материалам ОГЭ 140
Теорема Пифагора окрытый урок Теорема Пифагора окрытый урок 148
Презентация по геометрии на тему: Парабола (10 класс) Презентация по геометрии на тему: Парабола (10 класс) 173
Чудеса симметрии Чудеса симметрии 47
Решение комбинированных задач с помощью графов Решение комбинированных задач с помощью графов 194
Призма. Сечения призмы Призма. Сечения призмы 156
Отрезки Отрезки 140
Правильные многоугольники Правильные многоугольники 165
Фракталы и их применение в наши дни Фракталы и их применение в наши дни 149
Египетские пирамиды Египетские пирамиды 182
Зачетная система по геометрии в 8 классе Зачетная система по геометрии в 8 классе 146
Зарождение геометрии и её история Зарождение геометрии и её история 157
Презентация по геометрии в 7 классе Презентация по геометрии в 7 классе 165