Презентация на тему Координаты вектора

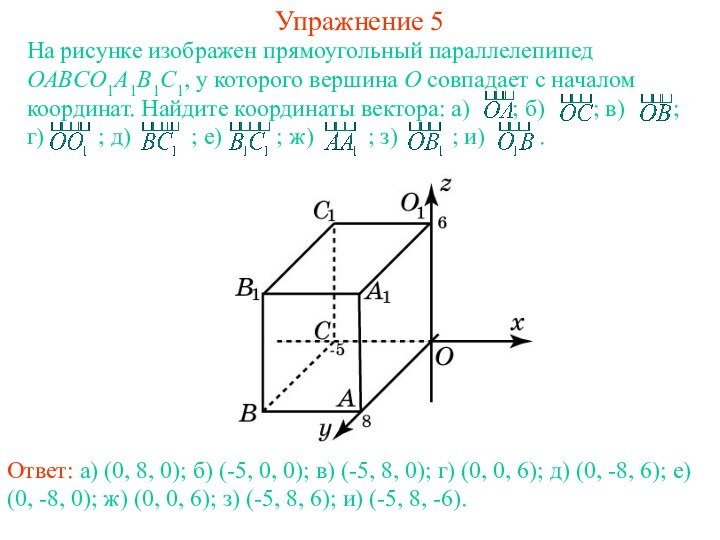
z) тогда и только тогда, когда он представим в

Доказательство. Отложим вектор от начала координат и его конец обозначим через А. Имеет место равенство

Точка А имеет координаты (x, y, z) тогда и только тогда, когда выполняются равенства

и, значит,

координатами начальной и конечной точек, A1(x1, y1, z1), A2(x2,

Ответ: а) (-2, 6, 1);

б) (1, 3, 0);

в) (0, -3, 2);

г) (-5, 0, 5).

, если: a) A(2, -6, 9), B(-5, 3,

Ответ: а) (-7, 9, -16);

б) (5, -8, -2);

в) (8, 0, 19).

(a,b,c). Найдите координаты вектора .
Ответ: (-a,

начало координат, ребра OA, OC, OO1 лежат на осях

Ответ: (2, 0, 4); (2, 3, 4); (0, 0, 4); (0, 3, 0).

которого вершина O совпадает с началом координат. Найдите координаты

Ответ: а) (0, 8, 0); б) (-5, 0, 0); в) (-5, 8, 0); г) (0, 0, 6); д) (0, -8, 6); е) (0, -8, 0); ж) (0, 0, 6); з) (-5, 8, 6); и) (-5, 8, -6).

и , если

Ответ: (1, 3, -2); (1, -3, 6).

(2,-4,3). Найдите координаты векторов:
а)

имеет координаты (4, -3, 0)

Ответ: (5, -6, -7).

он был: а) перпендикулярен координатной плоскости Oxy; б) параллелен

Ответ: а) Первая и вторая координаты равны нулю;

б) вторая и третья координаты равны нулю.

в точке A(1, 2, 3) и: а) перпендикулярного плоскости

Ответ: а) (1,2,4), (1,2,2);

б) (2,2,3), (0,2,3).