- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теорема Пифагора, история, формулировка, доказательства
Содержание
- 2. Содержание История теоремыФормулировка теоремы Доказательства теоремы Значение теоремы Пифагора
- 3. История теоремы Исторический обзор начнем с древнего Китая. Здесь
- 4. Кантор (крупнейший немецкий историкматематики) считает,
- 5. Очень легко можно
- 6. Несколько больше известно о теореме Пифагора у вавилонян.
- 7. Формулировка теоремы« Доказать, что квадрат, построенный
- 8. Современная формулировка« В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».
- 9. Доказательства теоремы Существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.).
- 10. Самое простое доказательствоРассмотрим квадрат, показанный на рисунке. Сторона квадрата равна a + c. ca
- 11. В одном случае (слева) квадрат
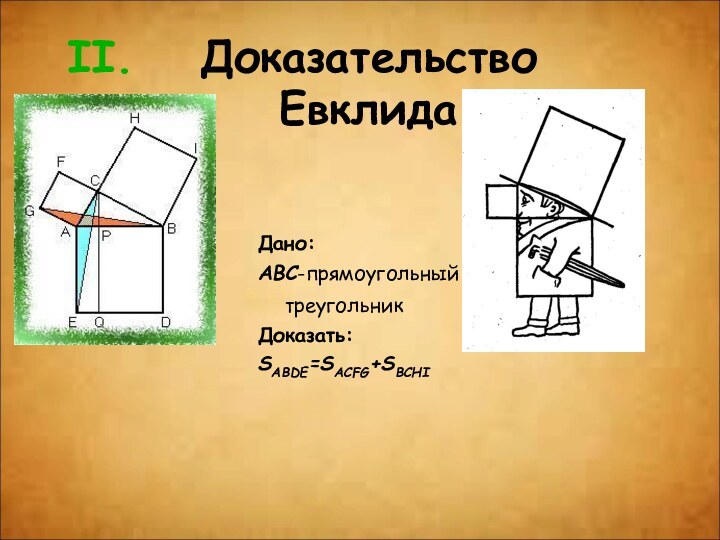
- 12. Доказательство Евклида Дано: ABC-прямоугольный треугольник Доказать:SABDE=SACFG+SBCHI
- 13. Доказательство: Пусть ABDE-квадрат, построенный на гипотенузе прямоугольного
- 14. Очевидно, что углы CAE=GAB(=A+90°); отсюда следует, что
- 15. Алгебраическое доказательствоДано: ABC-прямоугольный треугольникДоказать: AB2=AC2+BC2 Доказательство: 1) Проведем высоту
- 16. Геометрическое доказательство Дано: ABC-прямоугольный треугольникДоказать: BC2=AB2+AC2Доказательство: 1) Построим
- 17. Значение теоремы ПифагораТеорема Пифагора- это одна
- 18. Скачать презентацию
- 19. Похожие презентации












Слайд 2
Содержание
История теоремы
Формулировка теоремы
Доказательства теоремы
Значение теоремы
Пифагора
Слайд 3
История теоремы
Исторический обзор начнем с древнего Китая. Здесь особое внимание
привлекает математическая книга Чупей. В этом сочинении так говорится
о пифагоровом треугольнике со сторонами 3, 4 и 5:"Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4".
В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.
Слайд 4
Кантор (крупнейший немецкий историк
математики) считает, что
равенство
3 ² + 4 ² = 5²
было известно уже египтянам еще около 2300 г.
до н. э., во
времена царя Аменемхета I (согласнопапирусу 6619 Берлинского музея).
По мнению Кантора гарпедонапты, или
"натягиватели веревок", строили прямые углы
при помощи прямоугольных треугольников со
сторонами 3, 4 и 5.
Слайд 5 Очень легко можно воспроизвести
их способ построения. Возьмем веревку длиною в 12 м.
и привяжем к ней по цветной полоске на расстоянии 3м. от одного конца и 4 метра от другого . Прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра. Гарпедонаптам можно было бы возразить, что их способ построения становиться излишним, если воспользоваться, например, деревянным угольником, применяемым всеми плотниками. И действительно, известны египетские рисунки, на которых встречается такой инструмент, например рисунки, изображающие столярную мастерскую.Слайд 6 Несколько больше известно о теореме Пифагора у вавилонян. В
одном тексте, относимом ко времени Хаммураби, т. е. к
2000 г. до н. э., приводится приближенное вычисление гипотенузы прямоугольного треугольника. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере в некоторых случаях. Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой-на критическом изучении греческих источников,Ван-дер-Варден (голландский математик) сделал следующий вывод:
Слайд 7
Формулировка
теоремы
« Доказать, что квадрат, построенный на гипотенузе
прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах»
«
Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах». Во времена Пифагора теорема звучала так:
или
Слайд 8
Современная формулировка
« В прямоугольном треугольнике квадрат гипотенузы равен
сумме квадратов катетов».
Слайд 9
Доказательства теоремы
Существует около 500 различных доказательств
этой теоремы (геометрических, алгебраических, механических и т.д.).
Слайд 10
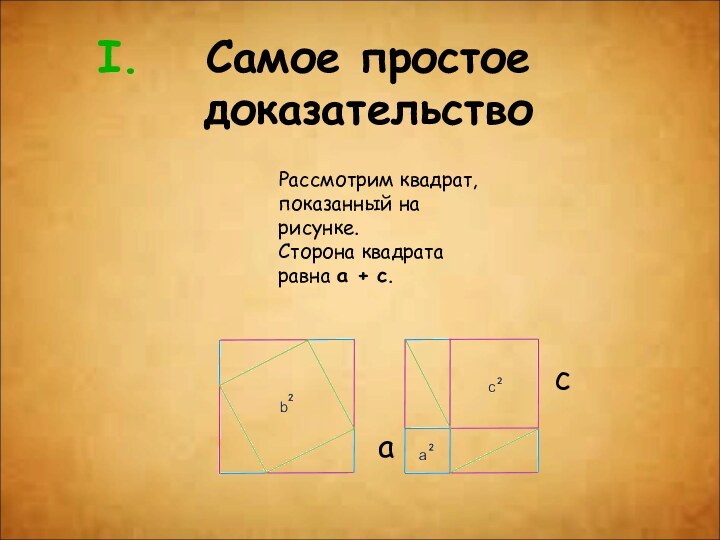
Самое простое доказательство
Рассмотрим квадрат, показанный на рисунке.
Сторона квадрата
равна a + c.
c
a
Слайд 11
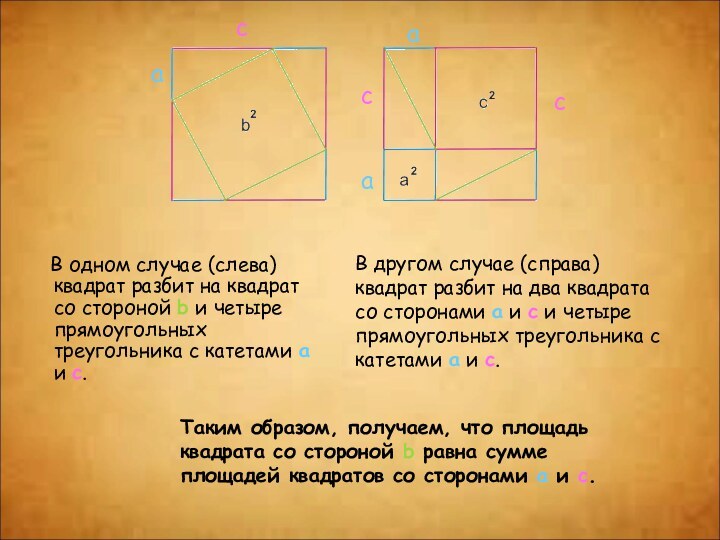
В одном случае (слева) квадрат разбит
на квадрат со стороной b и четыре прямоугольных треугольника
с катетами a и c.a
c
a
c
В другом случае (справа) квадрат разбит на два квадрата со сторонами a и c и четыре прямоугольных треугольника с катетами a и c.
a
c
Таким образом, получаем, что площадь квадрата со стороной b равна сумме площадей квадратов со сторонами a и c.
Слайд 13
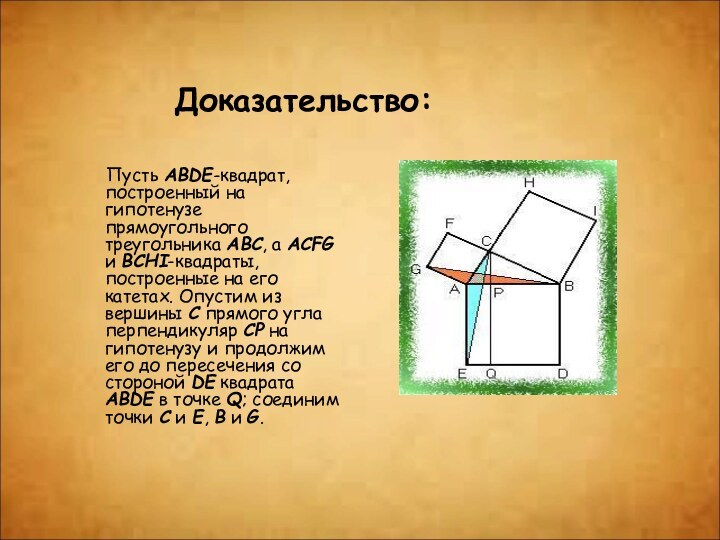
Доказательство:
Пусть ABDE-квадрат, построенный на гипотенузе прямоугольного треугольника
ABC, а ACFG и BCHI-квадраты, построенные на его катетах.
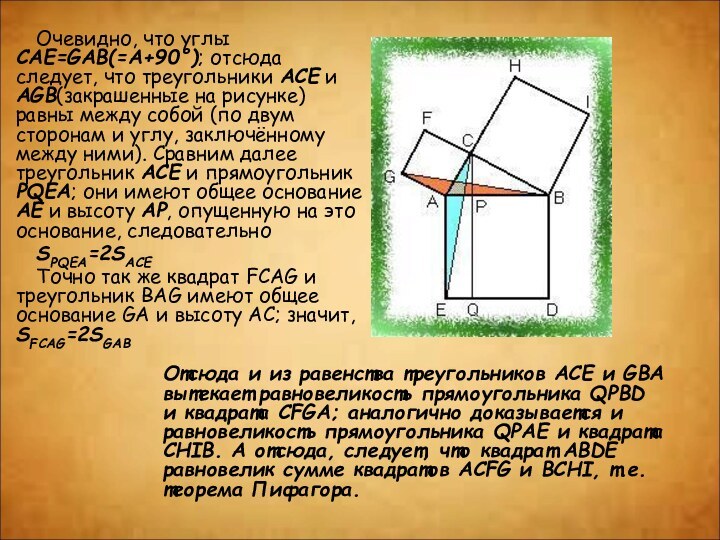
Опустим из вершины C прямого угла перпендикуляр CP на гипотенузу и продолжим его до пересечения со стороной DE квадрата ABDE в точке Q; соединим точки C и E, B и G.Слайд 14 Очевидно, что углы CAE=GAB(=A+90°); отсюда следует, что треугольники
ACE и AGB(закрашенные на рисунке) равны между собой (по
двум сторонам и углу, заключённому между ними). Сравним далее треугольник ACE и прямоугольник PQEA; они имеют общее основание AE и высоту AP, опущенную на это основание, следовательноSPQEA=2SACE
Точно так же квадрат FCAG и треугольник BAG имеют общее основание GA и высоту AC; значит, SFCAG=2SGAB
Отсюда и из равенства треугольников ACE и GBA вытекает равновеликость прямоугольника QPBD и квадрата CFGA; аналогично доказывается и равновеликость прямоугольника QPAE и квадрата CHIB. А отсюда, следует, что квадрат ABDE равновелик сумме квадратов ACFG и BCHI, т.е. теорема Пифагора.
Слайд 15
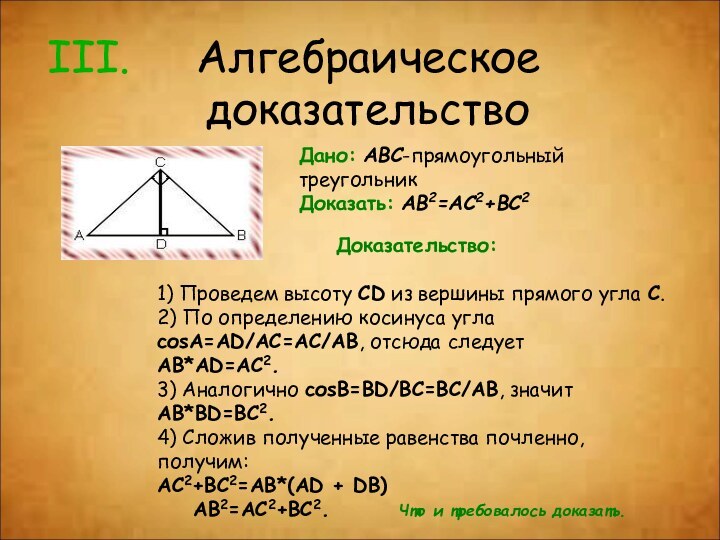
Алгебраическое доказательство
Дано: ABC-прямоугольный треугольник
Доказать: AB2=AC2+BC2
Доказательство:
1) Проведем высоту CD из
вершины прямого угла С. 2) По определению косинуса угла соsА=AD/AC=AC/AB, отсюда
следуетAB*AD=AC2.
3) Аналогично соsВ=BD/BC=BC/AB, значит
AB*BD=BC2.
4) Сложив полученные равенства почленно, получим:
AC2+BC2=АВ*(AD + DB)
AB2=AC2+BC2. Что и требовалось доказать.
Слайд 16
Геометрическое доказательство
Дано: ABC-прямоугольный треугольник
Доказать: BC2=AB2+AC2
Доказательство:
1) Построим отрезок CD
равный отрезку AB на продолжении катета AC прямоугольного треугольника
ABC. Затем опустим перпендикуляр ED к отрезку AD, равный отрезку AC, соединим точки B и E. 2) Площадь фигуры ABED можно найти, если рассматривать её как сумму площадей трёх треугольников:SABED=2*AB*AC/2+BC2/2
3) Фигура ABED является трапецией, значит, её площадь равна:
SABED= (DE+AB)*AD/2.
4) Если приравнять левые части найденных выражений, то получим:
AB*AC+BC2/2=(DE+AB)(CD+AC)/2
AB*AC+BC2/2= (AC+AB)2/2
AB*AC+BC2/2= AC2/2+AB2/2+AB*AC
BC2=AB2+AC2.
Это доказательство было опубликовано в 1882 году Гэрфилдом.





























