Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему Цилиндр. Конус

Содержание

2. Тема: «Цилиндр. Конус».Урок-КВН
3. 1. Закрепить полученные знания по теме :
4. Домашнее заданиеРазминкаРешение задачКонкурс капитановКонкурсы
5. Домашнее заданиеКонкурс
6. Историческая справка : Конус в переводе
7. Демокрит (470 - 380 гг. до н. э.) -
8. Аполлоний Пергский (260–170 гг. до н.э.) Большой
9. Детали машин , имеющие форму конуса:Конические подшипники качения (коробка передач, оси колес)Камеры карбюратораКонические резьбы (система охлаждения)
10. Историческая справка : Слово цилиндр происходит от
11. Платон (428–348 гг. до н.э.).
12. ПоршеньЦилиндрШейка коленчатого валаШейка распредвалаАмортизаторДетали машин имеющие форму цилиндра
13. РазминкаКонкурс
14. Покажите сечение цилиндра (конуса) плоскостью, проходящей через ось. Какая фигура получается в сечении?
15. Покажите сечение цилиндра (конуса) плоскостью, проходящей перпендикулярно к оси. Какая фигура получается в сечении?
16. Вращением какой фигуры можно получить конус (цилиндр) ?
17. Покажите угол между образующей конуса и его
18. Объясните, как построить линейный угол двугранного угла,
19. Как изменится площадь боковой поверхности конуса (цилиндра),
20. КонкурсРешение задач
21. Точки А и В расположены на видимой
22. L=5,r=4Найти hНайти элементы конуса (цилиндра )по готовым чертежам.АВ=20
23. Равнобедренный треугольник ABC вращается вокруг основания АС. АВ=m,
24. КапитановКонкурс
25. Задача . Высота конуса равна 10 см.
26. Задача . Плоскость параллельная оси цилиндра, отсекает
27. Подведение итогов
28. Задача №555 (а)
29. Скачать презентацию
30. Похожие презентации

Тема: «Цилиндр. Конус».Урок-КВН

Воробьева Оксана Владимировна Преподаватель математики ГБОУ СПО «ЗАМТ» г. Заволжье

1. Закрепить полученные знания по теме : «Цилиндр. Конус.»2. Формировать положительное отношение

Домашнее заданиеРазминкаРешение задачКонкурс капитановКонкурсы

Историческая справка : Конус в переводе с греческого

Демокрит (470 - 380 гг. до н. э.) - древнегреческий философ-материалист получил формулы

Аполлоний Пергский (260–170 гг. до н.э.) Большой трактат о конических сечениях был

Детали машин , имеющие форму конуса:Конические подшипники качения (коробка передач, оси колес)Камеры карбюратораКонические резьбы (система охлаждения)

Историческая справка : Слово цилиндр происходит от греческого слова

Платон (428–348 гг. до н.э.). Много сделала для геометрии школа

ПоршеньЦилиндрШейка коленчатого валаШейка распредвалаАмортизаторДетали машин имеющие форму цилиндра

Покажите сечение цилиндра (конуса) плоскостью, проходящей через ось. Какая фигура получается в сечении?

Покажите сечение цилиндра (конуса) плоскостью, проходящей перпендикулярно к оси. Какая фигура получается в сечении?

Вращением какой фигуры можно получить конус (цилиндр) ?

Покажите угол между образующей конуса и его осью. Равны ли эти углы?Покажите

Объясните, как построить линейный угол двугранного угла, образованного секущей плоскостью (МАВ) и

Как изменится площадь боковой поверхности конуса (цилиндра), если его образующую и радиус

Точки А и В расположены на видимой части боковой поверхности цилиндра (конуса).

L=5,r=4Найти hНайти элементы конуса (цилиндра )по готовым чертежам.АВ=20

Равнобедренный треугольник ABC вращается вокруг основания АС. АВ=m,

Задача . Высота конуса равна 10 см. Найдите площадь сечения, проходящего через

Задача . Плоскость параллельная оси цилиндра, отсекает от окружности основания дугу в

http://krabov.net/11878-10-velikih-matematikov-10-foto.htmlhttps://encrypted-tbn1.gstatic.com/images?q=tbn:ANd9GcTspfNnc0ieOPzkSd26xf7vB3lJWaoyKVWDt4zX4_1iHoy9j7kLHAhttp:///datai/algebra/Matematiki/0002-001-Arkhimed.jpghttps://encrypted-tbn0.gstatic.com/images?q=tbn:ANd9GcTqtFQFgJOTh5omDIP0GDUHTLQUUaWP-W7ZA_p0RZ_ueGbGSb5Khttp://img0.liveinternet.ru/images/foto/b/0/502/1415502/f_4819195.jpgИнтернет ресурсы

Слайды презентации

Слайд 2 Тема: «Цилиндр. Конус».
Урок-КВН

Слайд 3 1. Закрепить полученные знания по теме : «Цилиндр.

1. Закрепить полученные знания по теме : «Цилиндр. Конус.»2. Формировать положительное

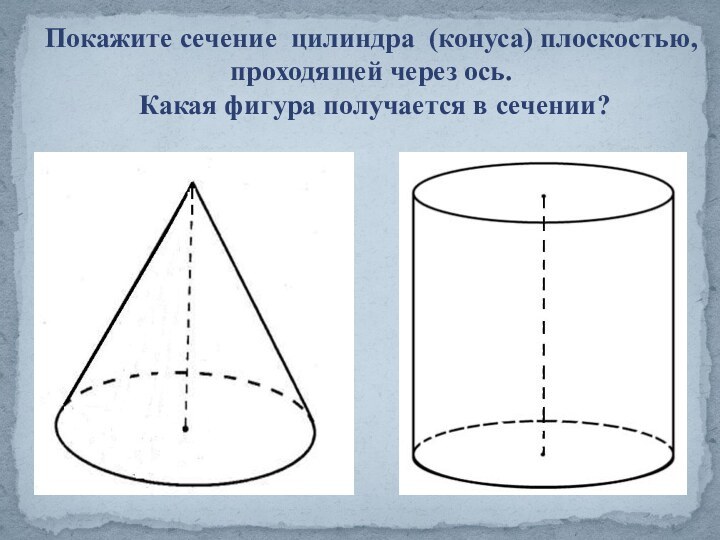
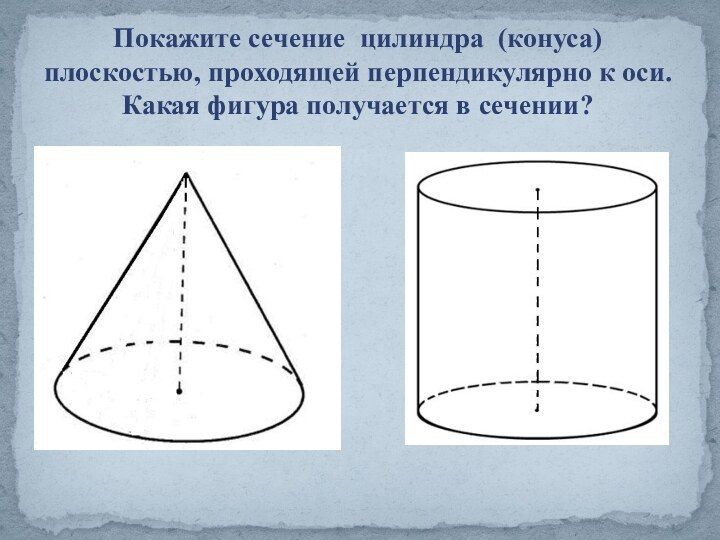
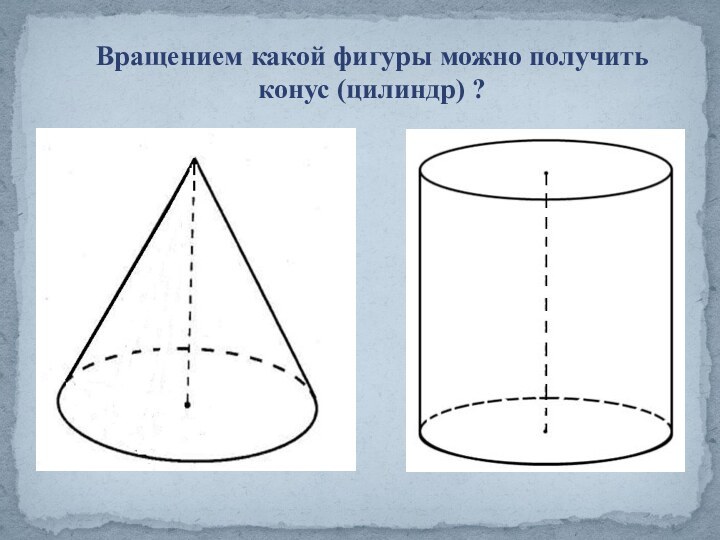
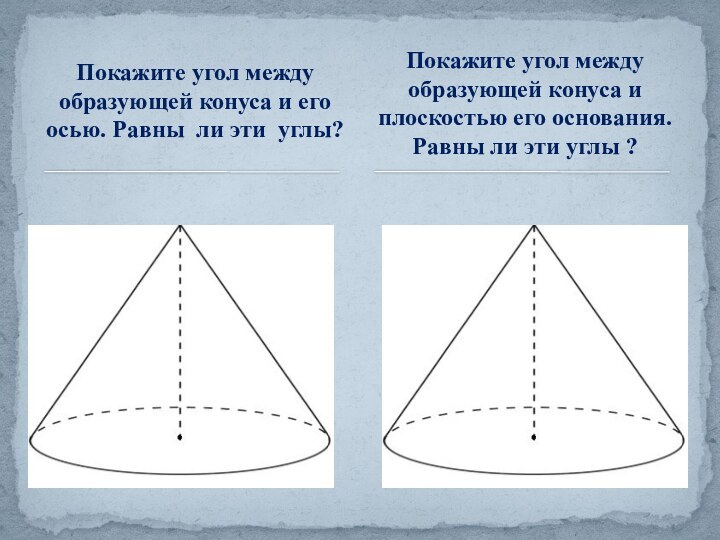
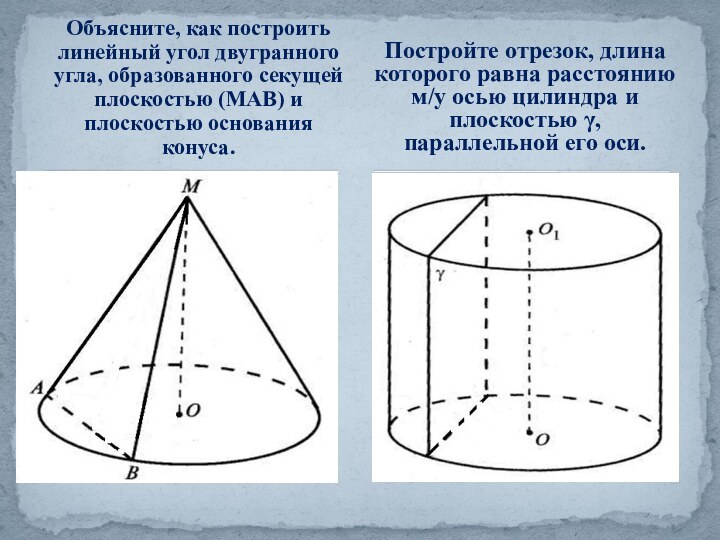
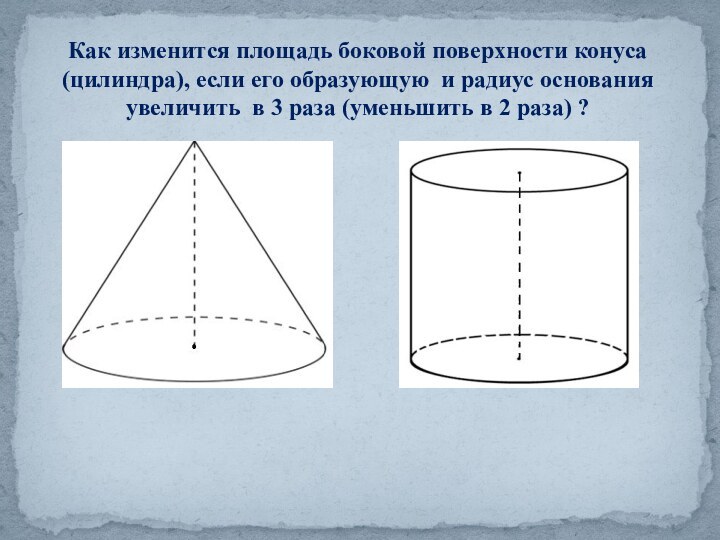
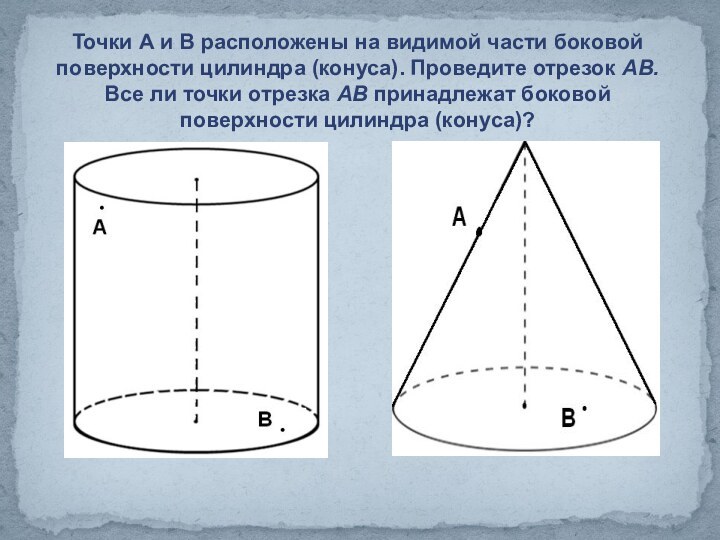
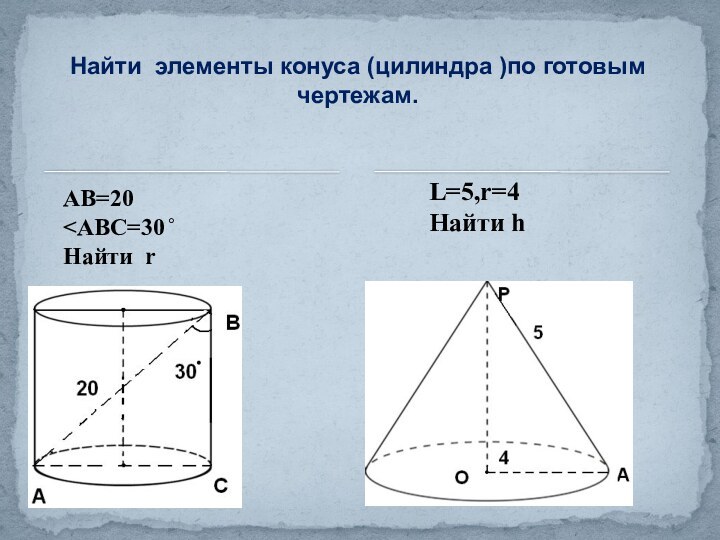
Конус.»
2. Формировать положительное отношение к знаниям, прививать интерес учащихся

к предмету.
Показать связь между математикой и профессией.
Воспитывать познавательную активность, культуру общения, культуру диалога.
Развивать математическую грамотность речи, логического мышления.

Цели и задачи:

Слайд 4 Домашнее задание
Разминка
Решение задач
Конкурс капитанов
Конкурсы

Слайд 5 Домашнее задание
Конкурс

Слайд 6 Историческая справка : Конус в переводе с

греческого "konos" означает "сосновая шишка".С конусом люди знакомы с

глубокой древности.

Платон
(428–348 гг. до н. э.)
Много сделала для геометрии школа Платона, в частности, ей принадлежит:
а) изучение конических сечений
б) исследование свойств призмы, пирамиды, цилиндра и конуса

Слайд 7 Демокрит
(470 - 380 гг. до н. э.) - древнегреческий

философ-материалист
получил формулы для вычисления объема пирамиды и

конуса.

Историческая справка

Слайд 8 Аполлоний Пергский
(260–170 гг. до н.э.)
Большой трактат

Аполлоний Пергский (260–170 гг. до н.э.) Большой трактат о конических сечениях

о конических сечениях был написан Аполлонием Пергским – учеником

Евклида (III в. до н.э.), который создал великий труд из 15 книг под названием “Начала”. Эти книги издаются и по сей день, а в школах Англии по ним учатся до сих пор.

Историческая справка

Слайд 9 Детали машин , имеющие форму конуса:
Конические подшипники качения

(коробка передач, оси колес)
Камеры карбюратора
Конические резьбы (система охлаждения)

Слайд 10 Историческая справка : Слово цилиндр происходит от греческого

слова

, что означает “валик”, “каток”. С цилиндром люди знакомы с глубокой древности.

Архимед
(287–212 гг. до н.э.)
В 1906 году была обнаружена книга Архимеда “О методе”, в которой дается решение задачи об объеме общей части пересекающихся цилиндров. Архимед приписывает честь открытия этого принципа – Демокриту (470–380 гг. до н.э.) – древнегреческому философу-материалисту.

Слайд 11 Платон (428–348 гг. до н.э.).
Много сделала для

Платон (428–348 гг. до н.э.). Много сделала для геометрии школа Платона.

геометрии школа Платона. Платон был учеником Сократа (470–399 гг.

до н.э.). В 387 г. до н.э. Платон основал в Африке Академию, в которой работал 20 лет. Каждый, входящий в Академию, читал надпись: “Пусть сюда не входит никто, не знающий геометрии”. Школе Платона принадлежит исследование свойств цилиндра.

Историческая справка