Презентация на тему Безусловная оптимизация методом классического математического анализа

химической реакции в аппарате идеального смешения, приняв в качестве

Схема реакции:

Порядок обеих стадий реакции – первый. Константы скоростей равны:

и P:
Решение

реагента v получаем:
где
- среднее время пребывания реагентов в реакторе

ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ

анализа.
Определение оптимальной температуры в непрерывном реакторе с мешалкой

обратимой двухкомпонентной реакции в реакторе с мешалкой, использовав в

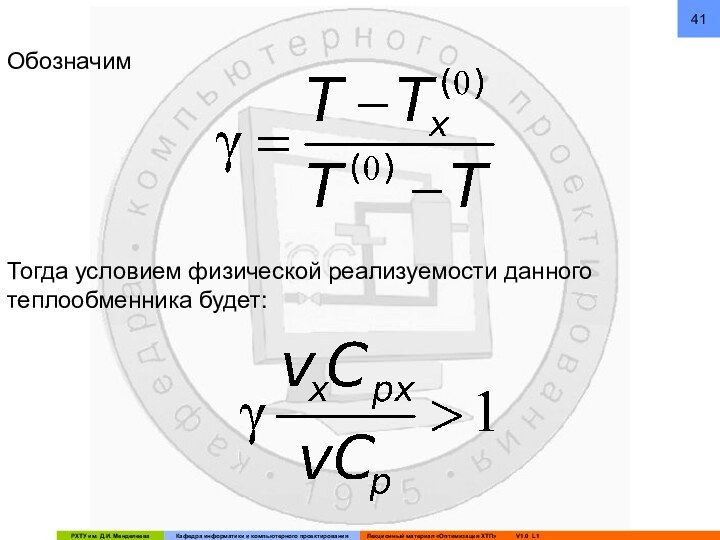
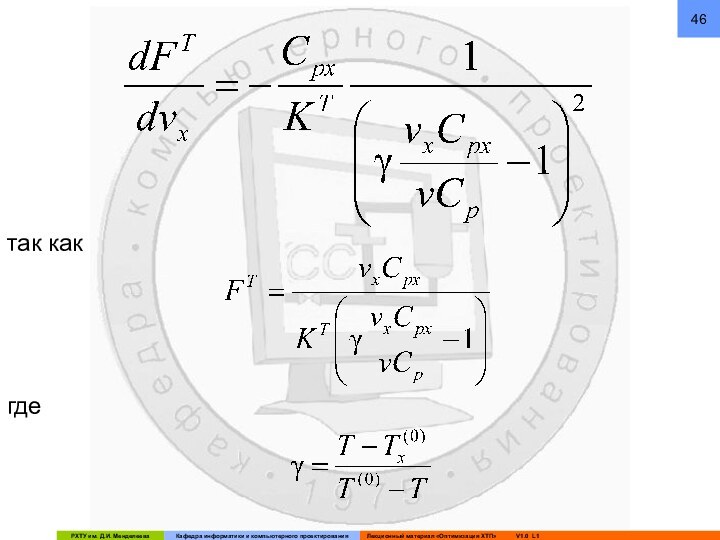
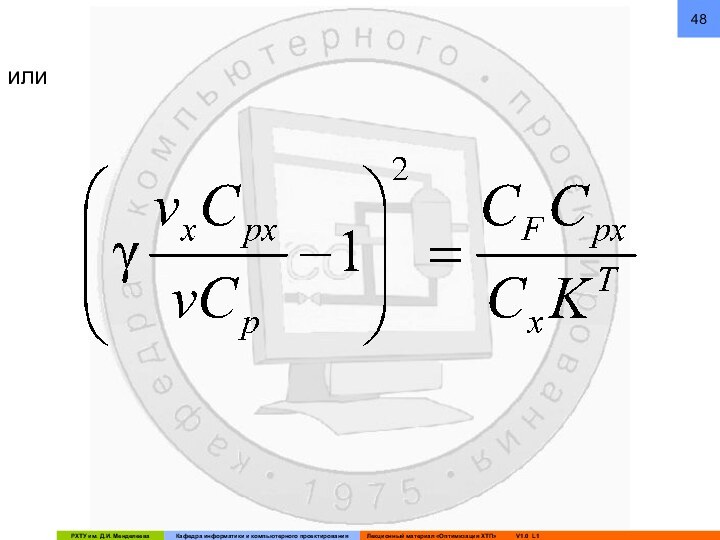
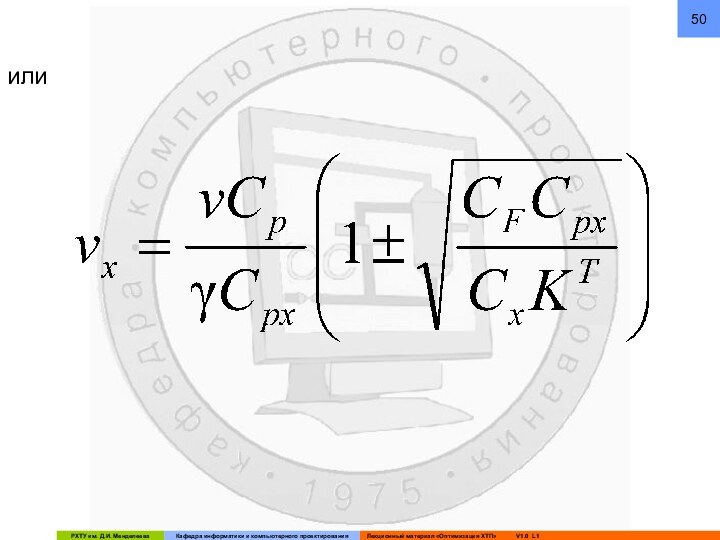
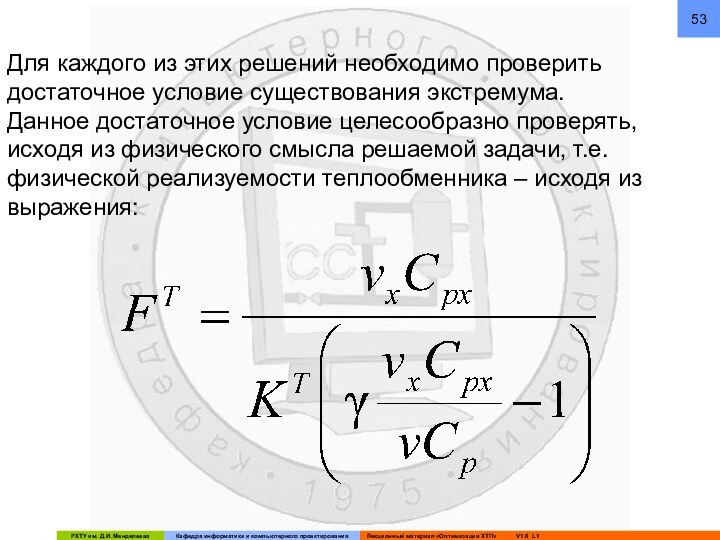
Схема реакции:

Порядок обеих стадий реакции – первый. Константы равны:

пребывания в реакторе:
Задача 3

и P для реактора идеального перемешивания:
Решение

определяется выражение для выхода компонента P:
где
- среднее время пребывания

нулю, получаем:

анализа.
Определение оптимального времени протекания процесса в периодическом реакторе с

реакции в периодическом реакторе с мешалкой, использовав в качестве

Схема реакции:

Порядок обеих стадий реакции – первый. Константы скоростей равны:

и P для периодического реактора:
Решение
Начальные условия:

разделяющимися переменными:

уравнение системы:

выражения на получаем дифференциальное

С начальными условиями:

методами даёт:

, получаем:

для , получаем максимально

ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ

анализа.
Определение оптимального расхода хладагента в теплообменнике смешение-смешение

в теплообменнике смешение-смешение и определить площадь поверхности теплопередачи при

Тх = ?

теплового баланса
Необходимо определить: = ? Vx

Для решения задачи оптимизации необходим конструкционный расчет

СЛАУ, которое решается относительно FT:

за скобки



получим:

Tx и FT.
Это означает, что температура T на

при определении Tx и FT известны и заданы.

– стоимость единицы расхода хладагента [руб/ед. массы] (в случае

В) Таким образом, ресурсами оптимизации – оптимизирующими переменными – являются vx и FT

необходимым условием функции одной переменной:

экстремума R получается:

в тех точках, где производная целевой функции R не

условие существования экстремума.
Данное достаточное условие целесообразно проверять, исходя

функцией, и достаточное условие существования экстремума выполняется.
Из трех возможных

выражение для FT(vx) получается: