- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Абстрактный автомат. Описание автомата
Содержание
- 2. Способы задания автоматаСуществуют два способа задания автомата:ТабличныйГрафовый
- 3. Табличный способ (1)При табличном описании задают две
- 4. Табличный способ (2) Обычно эти таблицы совмещают
- 5. Табличный способ (3)Таблицы абстрактного автомата совпадают с
- 6. Табличный способ (4): задание абстрактного недетерминированного автоматаВ
- 7. Табличный способ (5): задание недетерминированных автоматов Мили и МураТаблица 1.7Таблица 1.8
- 8. Задание автомата графом: определение таблиц соединения состояний
- 9. Задание автомата графом: таблицы соединения состоянийТаблицей 1.9
- 10. Задание автомата графом: условия использованияПри начертании графа
- 11. Скачать презентацию
- 12. Похожие презентации
Способы задания автоматаСуществуют два способа задания автомата:ТабличныйГрафовый Автоматы удобно описывать с помощью таблиц, а для наглядности использовать графы







Слайд 3
Табличный способ (1)
При табличном описании задают две таблицы,
одна из которых раскрывает функцию переходов (см. таблицу 1.1),
а другая - функцию выходов (см. таблицу 1.2)Число строк таблиц m равно числу состояний автомата, т.е. m = |Q|
Число столбцов таблиц n равно числу символов входного алфавита, т.е. n = |X|
В позиции первой таблицы записывают значения очередных состояний автомата q[τ+1]∈Q, в которые он переходит для каждой пары (q[τ], x[τ])∈(Q•X)
В позиции второй таблицы записывают значения символов выходного алфавита y[τ]∈Y, которые генерирует автомат для каждой пары (q[τ], x[τ])∈(Q•X)
Если в таблицах 1 и 2 определены значения q[τ+1]∈Q и
y[τ]∈Y для каждой пары (q[τ], x[τ])∈(Q•X), то есть заполнены все позиции таблиц, то дано описание детерминированного автомата
Слайд 4
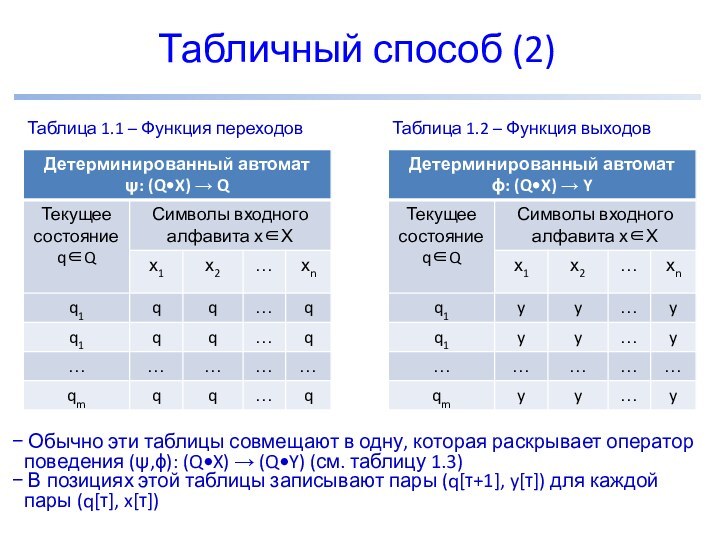
Табличный способ (2)
Обычно эти таблицы совмещают в
одну, которая раскрывает оператор поведения (ψ,ϕ):
(Q•X) → (Q•Y) (см. таблицу 1.3)В позициях этой таблицы записывают пары (q[τ+1], y[τ]) для каждой пары (q[τ], x[τ])
Таблица 1.1 – Функция переходов
Таблица 1.2 – Функция выходов
Слайд 5
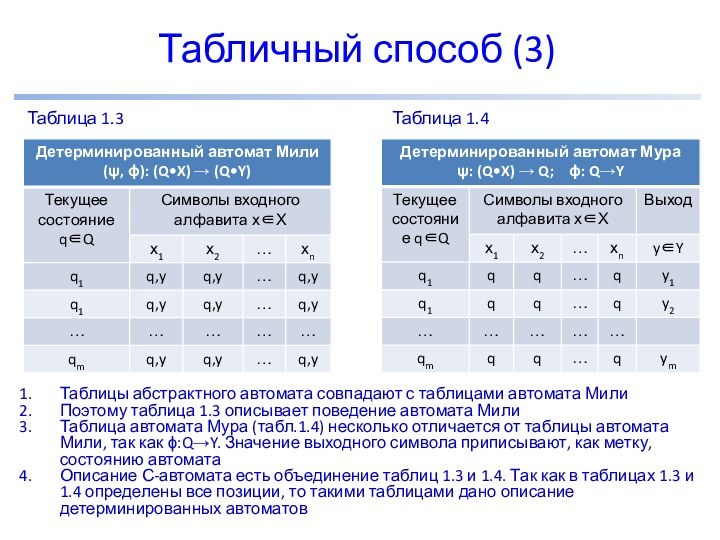
Табличный способ (3)
Таблицы абстрактного автомата совпадают с таблицами
автомата Мили
Поэтому таблица 1.3 описывает поведение автомата Мили
Таблица автомата
Мура (табл.1.4) несколько отличается от таблицы автомата Мили, так как ϕ:Q→Y. Значение выходного символа приписывают, как метку, состоянию автоматаОписание С-автомата есть объединение таблиц 1.3 и 1.4. Так как в таблицах 1.3 и 1.4 определены все позиции, то такими таблицами дано описание детерминированных автоматов
Таблица 1.3
Таблица 1.4
Слайд 6
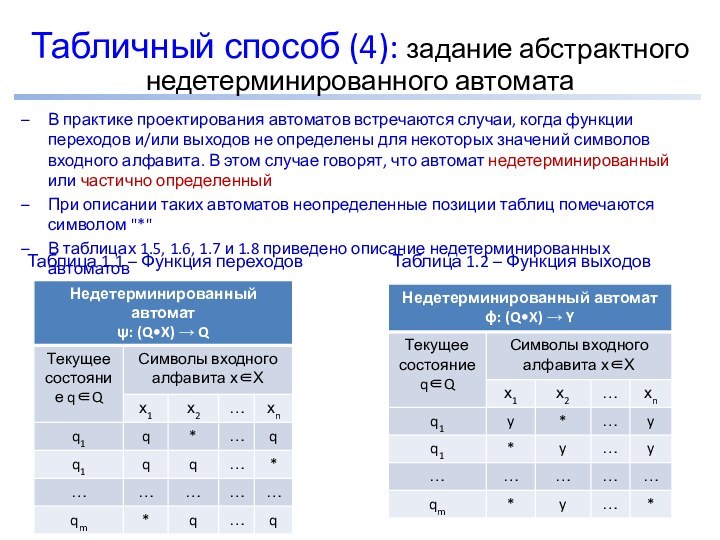
Табличный способ (4): задание абстрактного недетерминированного автомата
В практике
проектирования автоматов встречаются случаи, когда функции переходов и/или выходов
не определены для некоторых значений символов входного алфавита. В этом случае говорят, что автомат недетерминированный или частично определенныйПри описании таких автоматов неопределенные позиции таблиц помечаются символом "*"
В таблицах 1.5, 1.6, 1.7 и 1.8 приведено описание недетерминированных автоматов
Таблица 1.1 – Функция переходов
Таблица 1.2 – Функция выходов
Слайд 7 Табличный способ (5): задание недетерминированных автоматов Мили и
Мура
Таблица 1.7
Таблица 1.8
Слайд 8
Задание автомата графом: определение таблиц соединения состояний
Поведение
автомата удобно анализировать с помощью графов, вершинами которого являются
элементы множества q∈Q, тогдавершина-исток есть образ текущего состояния q[τ]
вершина-сток - образ очередного состояния q[τ+1]
дуги отображают переход автомата из одного состояния в другое (q[τ], q[τ+1]) под воздействием x[τ]∈X
Для описания автомата с помощью графов удобно воспользоваться таблицами соединений состояний автомата
Строки и столбцы такой таблицы представляют символы q∈Q
Число строк и столбцов таблицы равно m
Строки этой таблицы характеризуют текущее состояние, т.е. q[τ], а столбцы - очередное, т.е. q[τ+1]
Позиции таблицы заполняют значениями пары (x[τ]/y[τ]) для соответствующего перехода автомата из текущего состояния в очередное
Слайд 9
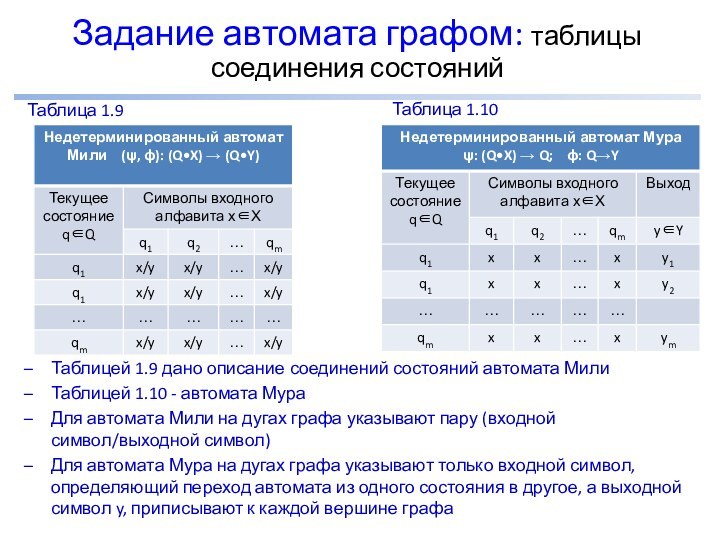
Задание автомата графом: таблицы соединения состояний
Таблицей 1.9 дано
описание соединений состояний автомата Мили
Таблицей 1.10 - автомата
МураДля автомата Мили на дугах графа указывают пару (входной символ/выходной символ)
Для автомата Мура на дугах графа указывают только входной символ, определяющий переход автомата из одного состояния в другое, а выходной символ y, приписывают к каждой вершине графа
Таблица 1.9
Таблица 1.10
Слайд 10
Задание автомата графом: условия использования
При начертании графа детерминированного
автомата следует соблюдать следующие условия:
для каждого символа x∈X есть
дуга, исходящая из вершины q∈Q каждый символ x∈X у каждой вершины-истока q∈Q принадлежит только одной дуге
если между двумя вершинами q∈Q существует несколько дуг, что может быть обусловлено переходом автомата из состояния qs∈Q в состояние qt∈Q при различных символах на входе, то есть xi ≠xj, то эти дуги могут быть заменены одной дугой с указанием дизъюнктивной связи этих состояний например
если yu≠yv, то на дуге следует указать (xi/yu ∨ xj/ yv)
если yu=yv=y, то - (xi∨xj)/y)





























