Презентация на тему Алгоритм Лемпеля - Зива - Велче

универсальный алгоритм сжатия данных без потерь, созданный Авраамом Лемпелем,

Яаковом Зивом и Терри Велчем .
Он был опубликован Велчем в 1984 году, в качестве улучшенной реализации алгоритма LZ78, опубликованного Лемпелем и Зивом в 1978 году. Алгоритм разработан так, чтобы его можно было быстро реализовать, но он не обязательно оптимален, поскольку он не проводит никакого анализа входных данных.
Акроним «LZW» указывает на фамилии изобретателей алгоритма: Лемпель, Зив и Велч.

преобразования строк:
определённым последовательностям символов (словам) ставятся в соответствие

группы бит фиксированной длины (обычно 12-битные).
Таблица инициализируется всеми 1-символьными строками (в случае 8-битных символов — это 256 записей). По мере кодирования алгоритм просматривает текст символ за символом, и сохраняет каждую новую, уникальную 2-символьную строку в таблицу в виде пары код/символ, где код ссылается на соответствующий первый символ.
После того как новая 2-символьная строка сохранена в таблице, на выход передаётся код первого символа. Когда на входе читается очередной символ, для него по таблице находится уже встречавшаяся строка максимальной длины, после чего в таблице сохраняется код этой строки со следующим символом на входе;
на выход выдаётся код этой строки, а следующий символ используется в качестве начала следующей строки.

текст, поскольку он может воссоздать соответствующую таблицу преобразования непосредственно

по закодированному тексту

фразы W первым символом сообщения.
Найти в словаре строку W

наибольшей длины, которая совпадает с последними принятыми символами.
Считать очередной символ K из кодируемого сообщения.
Если КОНЕЦ_СООБЩЕНИЯ, то выдать код для W, иначе.
Если фраза WK уже есть в словаре, присвоить входной фразе W значение WK и перейти к Шагу 3, иначе выдать код W, добавить WK в словарь, присвоить входной фразе W значение K и перейти к Шагу 3.
Конец.

коэффициент сжатия, для большинства приложений, чем любой другой хорошо

известный метод того времени. Он стал первым широко используемым на компьютерах методом сжатия данных.
Алгоритм был реализован в программе compress, которая стала более или менее стандартной утилитой Unix-систем приблизительно в 1986 году. Несколько других популярных утилит-архиваторов также используют этот метод или близкие к нему.

состояние выходных данных и словаря на каждой стадии, как

при кодировании, так и при раскодировании сообщения. С тем чтобы сделать изложение проще, мы ограничимся простым алфавитом — только заглавные буквы, без знаков препинания и пробелов. Сообщение, которое нужно сжать, выглядит следующим образом:

самым, в нашем алфавите 27 символов (26 заглавных букв

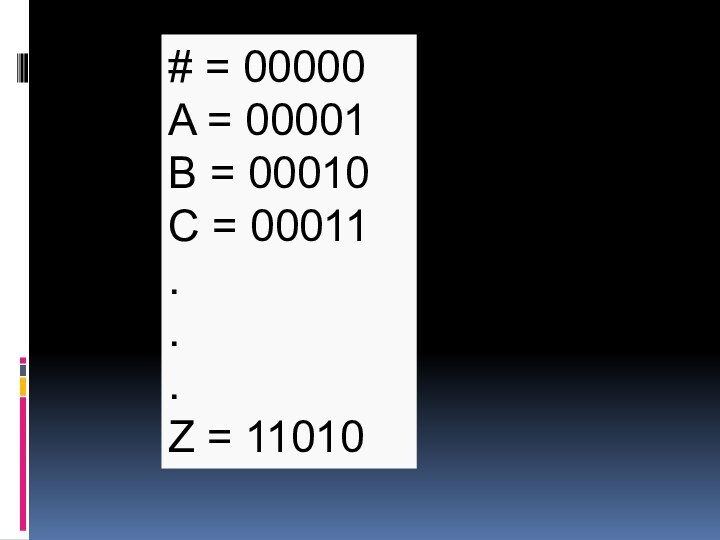
от A до Z и #). Компьютер представляет это в виде групп бит, для представления каждого символа алфавита нам достаточно группы из 5 бит на символ. По мере роста словаря, размер групп должен расти, с тем чтобы учесть новые элементы. 5-битные группы дают 25 = 32 возможных комбинации бит, поэтому, когда в словаре появится 33-е слово, алгоритм должен перейти к 6-битным группам. Заметим, что, поскольку используется группа из всех нулей 00000, то 33-я группа имеет код 32. Начальный словарь будет содержать:

00011
.
.
.
Z = 11010

оно есть — 25 символов по 5 бит на

каждый — оно займёт 125 бит. Сравним это с тем, что получается при использовании LZW:

(на выходе) 
T 20 = 10100
O 15 = 01111 27: TO
B 2 = 00010 28: OB
E 5 = 00101 29: BE
O 15 = 01111 30: EO
R 18 = 10010 31: OR <--- со следующего символа начинаем использовать 6-битные группы
N 14 = 001110 32: RN
O 15 = 001111 33: NO
T 20 = 010100 34: OT
TO 27 = 011011 35: TT
BE 29 = 011101 36: TOB
OR 31 = 011111 37: BEO
TOB 36 = 100100 38: ORT
EO 30 = 011110 39: TOBE
RN 32 = 100000 40: EOR
OT 34 = 100010 41: RNO
# 0 = 000000 42: OT#
 

бит.
Таким образом, используя LZW, мы сократили сообщение на 29

бит из 125 — это почти 22 %. Если сообщение будет длиннее, то элементы словаря будут представлять всё более и более длинные части текста, благодаря чему повторяющиеся слова будут представлены очень компактно

сообщение, приведённое выше, и нам нужно его декодировать. Прежде

всего, нам нужно знать начальный словарь, а последующие записи словаря мы можем реконструировать уже на ходу, поскольку они являются просто конкатенацией предыдущих записей.

Новая запись: : Частичная:
10100

= 20 T 27: T?
01111 = 15 O 27: TO 28: O?
00010 = 2 B 28: OB 29: B?
00101 = 5 E 29: BE 30: E?
01111 = 15 O 30: EO 31: O?
10010 = 18 R 31: OR 32: R? <---- начинаем использовать 6-битные группы
001110 = 14 N 32: RN 33: N?
001111 = 15 O 33: NO 34: O?
010100 = 20 T 34: OT 35: T?
011011 = 27 TO 35: TT 36: TO? <---- для 37, добавляем только первый элемент
011101 = 29 BE 36: TOB 37: BE? следующего слова словаря
011111 = 31 OR 37: BEO 38: OR?
100100 = 36 TOB 38: ORT 39: TOB?
011110 = 30 EO 39: TOBE 40: EO?
100000 = 32 RN 40: EOR 41: RN?
100010 = 34 OT 41: RNO 42: OT?
000000 = 0 #

новое слово словаря пересылается немедленно. В приведённом выше примере

декодирования, когда декодер встречает первый символ, T, он знает, что слово 27 начинается с T, но чем оно заканчивается? Проиллюстрируем проблему следующим примером. Мы декодируем сообщение ABABA:

запись:

Полная: Частичная:
.
.
.
011101 = 29 AB 46: (word) 47: AB?
101111 = 47 AB? <--- что нам с этим делать?

Мы знаем наперёд, что словом 47 должно быть ABA,

но как декодер узнает об этом? Заметим, что слово 47 состоит из слова 29 плюс символ, идущий следующим. Таким образом, слово 47 заканчивается на «символ, идущий следующим». Но, поскольку это слово посылается немедленно, то оно должно начинаться с «символа, идущего следующим», и поэтому оно заканчивается тем же символом, что и начинается, в данном случае — A. Этот трюк позволяет декодеру определить, что слово 47 — это ABA.
В общем случае, такая ситуация появляется, когда кодируется последовательность вида cScSc, где c — это один символ, а S — строка, причём слово cS уже есть в словаре.