Слайд 2
План лекции
Понятие двумерного статического массива
Ввод – вывод элементов
массива
Заполнение массива случайными числами
Квадратные матрицы
Транспонирование матриц
Умножение матрицы на вектор
Умножение
матрицы на матрицу
Удаление строки
Включение столбца
Операции с элементами матриц
Преобразование матрицы в одномерный массив
Многомерные массивы
Слайд 3
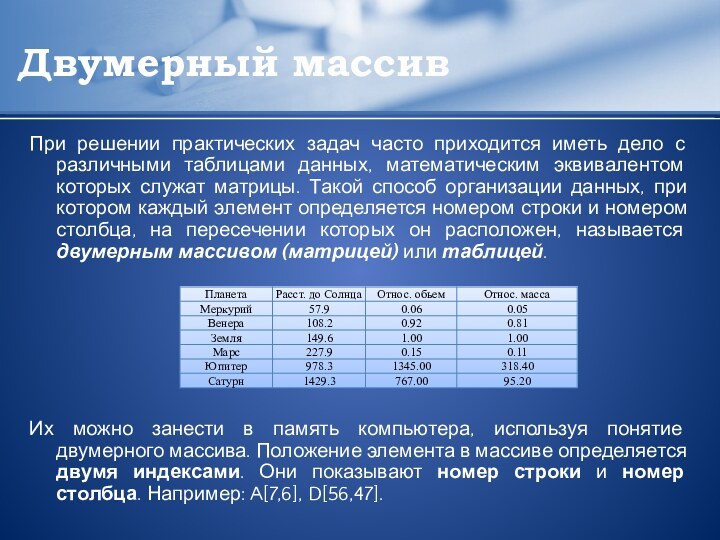
Двумерный массив
При решении практических задач часто приходится иметь
дело с различными таблицами данных, математическим эквивалентом которых служат
матрицы. Такой способ организации данных, при котором каждый элемент определяется номером строки и номером столбца, на пересечении которых он расположен, называется двумерным массивом (матрицей) или таблицей.
Их можно занести в память компьютера, используя понятие двумерного массива. Положение элемента в массиве определяется двумя индексами. Они показывают номер строки и номер столбца. Например: A[7,6], D[56,47].
Слайд 4
Пример объявления двумерного массива
Организацию обработки элементов статического двумерного
(многомерного) массива можно организовать с использованием сложноциклической структуры. Так
как, например, при заполнении массива необходимо произвести обход всех элементов по строкам ( i ) изменяя индексы столбцов ( j ). Таким образом объявленный массив из N строк и M столбцов
Const
n=6;
m=8;
Var
a : array [1..n, 1..m] of integer;
будет организован в памяти ЭВМ следующим образом:
Слайд 5
Ввод – вывод элементов двумерного массива
Const
n=6;
m=8;
Var
a : array
[1..n, 1..m] of integer;
I, j : integer;
Begin
writeln (‘ Заполнение
элементов целочисленного массива A[6,8] ‘);
for i:=1 to n do
for j:=1 to m do
begin
write (‘a[‘, i , ‘, ‘ , j, ‘] =‘);
read (a[ i , j ]);
end;
writeln (‘В памяти компьютера сформирован двумерный массив с элементами’);
for i:=1 to n do
begin
for j:=1 to m do
write (a[ i , j ]:6);
writeln;
end
End.
начало
Aij
A[6,8]
конец
Aij
Слайд 6
Ввод – вывод элементов двумерного массива
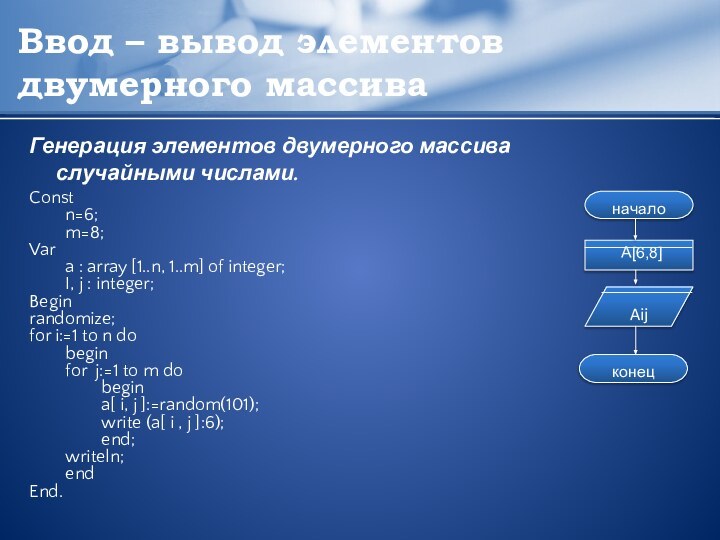
Генерация элементов двумерного
массива случайными числами.
Const
n=6;
m=8;
Var
a : array [1..n, 1..m] of integer;
I,
j : integer;
Begin
randomize;
for i:=1 to n do
begin
for j:=1 to m do
begin
a[ i, j ]:=random(101);
write (a[ i , j ]:6);
end;
writeln;
end
End.
начало
Aij
A[6,8]
конец
Слайд 7
Квадратные матрицы
В квадратной матрице количество строк и столбцов
- одинаково и равно n.
Любая квадратная матрица имеет
элементы главной и побочной диагонали.
Диагональные элементы главной диагонали :
a[1 , 1];a[2 , 2];a[3 , 3];….;a[n , n].
Элементами побочной диагонали являются :
a[1 , n];a[2 , n-1];a[3 , n-2];…;a[n-1 , 2];a[n , 1].
Слайд 8
Квадратные матрицы
В качестве примера рассмотрим задачу формирования квадратной
матрицы порядка n случайными числами и нахождения произведения элементов
главной диагонали и суммы элементов ниже побочной диагонали.
Отметим элементы главной диагонали для нахождения их произведения.
Слайд 9
Квадратные матрицы
И элементы ниже побочной диагонали для поиска
их суммы.
Слайд 10
Квадратные матрицы
Const
n=9;
Var
a : array [1..n, 1..n] of integer;
I,
j, s, p : integer;
Begin
randomize;
for i:=1 to n do
begin
for j:=1 to n do
begin
a[ i, j ]:=random(101);
write (a[ i , j ]:6);
end;
writeln;
end
p:=1;
for i:=1 to n do
p:=p*a[ i, i ];
s:=0;
for i:=2 to n do
for j:=n-i+2 to n do
s:=s+a[ i, j ];
writeln (p,s);
End.
Слайд 11
Транспонирование матриц
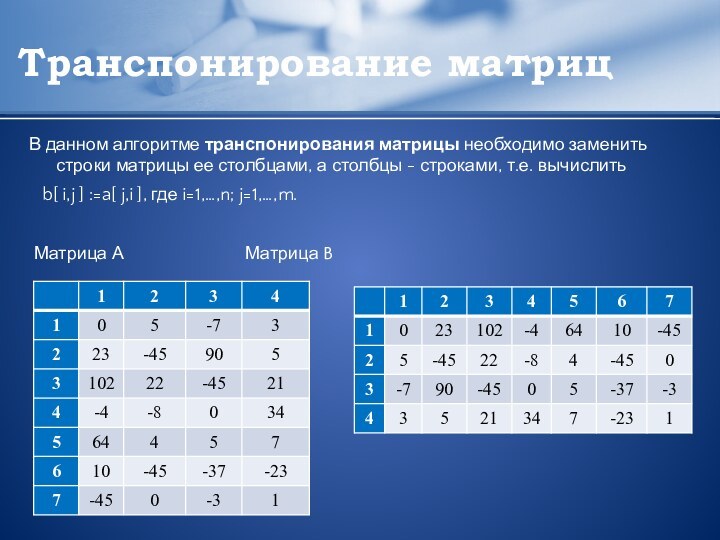
В данном алгоритме транспонирования матрицы необходимо заменить
строки матрицы ее столбцами, а столбцы - строками, т.е.
вычислить
b[ i,j ] :=a[ j,i ], где i=1,…,n; j=1,…,m.
Матрица А Матрица B
Слайд 12
Транспонирование матриц
Const
n=5;
m=7;
Var
i, j : integer;
a : array
[1..n,1..m] of integer;
b : array [1..m,1..n] of integer;
Begin
randomize;
writeln (‘Сформирована
матрица A’);
for i:=1 to n do
begin
for j:=1 to m do
begin
a[ i,j ]:=random(31)-15;
write (a[ i,j ]:6);
end;
writeln(‘’);
end;
for i:=1 to n do
for j:=1 to m do
b[ j,i ]:=a[ i,j ];
writeln (‘Получена транспонированная матрица B’);
for i:=1 to m do
begin
for j:=1 to n do
write(b[ i,j ]:6);
writeln(‘’);
end;
End.
Слайд 13
Транспонирование матриц
Транспонированную матрицу можно получить в исходном массива
А. Для квадратной матрицы n*n для этого необходимо поменять
местами каждый элемент верхнего треугольника с соответствующим элементом нижнего (диагональные элементы переставлять не нужно).
При этом для каждой строки нужно выполнять перестановку для элементов, расположенных правее главной диагонали, с элементами соответствующего столбца, расположенными ниже главной диагонали. При перестановке используем вспомогательную переменную tmp, помещая в нее для временного хранения один из переставляемых элементов, чтобы не потерять его значение.
Слайд 14
Транспонирование матриц
Const
n=9;
Var
i, j, tmp : integer;
a :
array [1..n,1..n] of integer;
Begin
randomize;
writeln (‘Сформирована квадратная матрица A’);
for i:=1
to n do
begin
for j:=1 to n do
begin
a[ i,j ]:=random(101)-50;
write (a[ i,j ]:6);
end;
writeln(‘’);
end;
for i:=1 to n-1 do
for j:=i+1 to n do
begin
tmp:=a[ i,j ];
a[ i,j ]:=a[ j,i ];
a[ j,i ]:=tmp;
end;
writeln (‘Получена транспонированная матрица ’);
for i:=1 to n do
begin
for j:=1 to n do
write(a[ i,j ]:6);
writeln(‘’);
end;
End.
Слайд 15
Умножение матрицы на вектор
Для вычисления произведения С матрицы
А размером n*m на вектор B
размером
m необходимо вычислить , i=1,….,n.
Использование вспомогательной переменной s позволяет уменьшить время выполнения программы за счет исключения обращения в цикле по j к элементам массива C.
Слайд 16
Умножение матрицы на вектор
Const
n=6;
m=9;
Var
i, j, s : integer;
a : array [1..n,1..m] of integer;
b : array [1..m]
of integer;
c: array [1..n] of integer;
Begin
randomize;
writeln (‘Сформирована матрица A’);
for i:=1 to n do
begin
for j:=1 to m do
begin
a[ i,j ]:=random(101)-50;
write (a[ i,j ]:6);
end;
writeln(‘’);
end;
writeln (‘Сформирован вектор B’);
for j:=1 to m do
begin
b[ j ]:=random(51)-30;
write (b[ j ]:6);
end;
for i:=1 to n do
begin
s:=0;
for j:=1 to m do
s:=s+a[ i,j ]*b[ j ];
c[ i ]:=s;
end;
writeln (‘Получен вектор C ’);
for i:=1 to n do
write(c[ i ]:6);
End.
Слайд 17
Умножение матрицы на матрицу
Для умножения матрицы А размером
n*k на матрицу B размером k*m
необходимо вычислить , i=1,…,n; j=1,…,m.
Const
n=3;
m=4;
k=5;
Var
i, j, s : integer;
a : array [1..n,1..k] of integer;
b : array [1..k,1..m] of integer;
c : array [1..n,1..m] of integer;
Begin
randomize;
writeln (‘Сформирована матрица A’);
for i:=1 to n do
begin
for j:=1 to k do
begin
a[ i,j ]:=random(101)-50;
write (a[ i,j ]:6);
end;
writeln;
end;
writeln (‘Сформирована матрица B’);
for i:=1 to k do
begin
for j:=1 to m do
begin
b[ i,j ]:=random(351)-85;
Слайд 18
Умножение матрицы на матрицу
write (a[ i,j ]:6);
end;
writeln();
end;
for i:=1
to n do
for j:=1 to m do
begin
s:=0;
for l:=1 to
k do
s:=s+a[ i,l ]*b[ l,j ];
c[ i,j ]:=s;
end;
writeln (‘Сформирована матрица С’);
for i:=1 to n do
begin
for j:=1 to m do
write (c[ i,j ]:6);
writeln;
end
End.
Слайд 19
Удаление строки матрицы
Алгоритм удаления строки является сходным с
алгоритмом удаление элементов одномерного массива, за тем исключением, что
операция переноса элементов выполняется для каждого столбца при переборе строк. Рассмотрим программу удаления из матрицы А заданной с клавиатуры строки T.
Const
n=10;
m=5;
Var
i, j, t, n : integer;
a : array [1..n,1..m] of integer;
Begin
randomize;
writeln (‘Сформирована матрица A’);
for i:=1 to n do
begin
for j:=1 to m do
begin
a[ i,j ]:=random(101)-50;
write (a[ i,j ]:6);
end;
writeln;
end;
writeln (‘Введите номер строки для удаления’);
readln (t);
Слайд 20
Удаление строки матрицы
k:=n-1;
for i:=t to k do
for j:=1
to m do
a[ i,j ]=a[ i+1,j ];
writeln (‘Получена
матрица ‘);
for i:=1 to k do
begin
for j:=1 to m do
write (a[ i,j ]);
writeln;
end
End.
Слайд 21
Включение столбца в матрицу
Алгоритм включения столбца в матрицу
является сходным с алгоритмом включения элементов одномерного массива, за
тем исключением, что операция переноса элементов выполняется для каждой строки при переборе столбцов. Рассмотрим пример, где необходимо в квадратной матрице А вставить столбец, содержащий ее элементы главной диагонали - следующим за столбцом, содержащим минимальный элемент матрицы. Для этого перепишем диагональные элементы в массив B, найдем минимальный элемент и его индекс по столбцу. Перебирая столбцы, сдвинем все столбцы на позицию вправо начиная от найденного индекса столбца минимального элемента. Занесем в следующий столбец за индексом минимального элемента - элементы столбца, которые хранятся в массиве B.
Слайд 22
Включение столбца в матрицу
Const
n=7;
Var
i, j, min, j_min, m:
integer;
a : array [1..n,1..n+1] of integer;
b : array
[1..n] of integer;
Begin
randomize;
writeln (‘Сформирована матрица A’);
for i:=1 to n do
begin
for j:=1 to n do
begin
a[ i,j ]:=random(101);
write (a[ i,j ]:6);
end;
b[ i ]:=a[ i,i ];
writeln;
end;
min:=a[1,1]; j_min:=1;
for i:=1 to n do
for j:=1 to n do
if (a[ i,j ] begin
min:=a[ i,j ];
j_min:=j;
end;
m:=n+1;
for j:=n downto j_min do
for i:=1 to n do
a[ i,j ]:=a[ i,j+1 ];
for i:=1 to n do
a[ i,j_min+1]:=b[ i ];
writeln (‘Получен массив ‘);
for i:=1 to n do
begin
for j:=1 to m do
write (a[ i,j ]:4);
writeln;
end
End.
Слайд 23
Операции с элементами матриц
Предыдущий пример может служить так
же и примером преобразования матрицы, однако довольно часто встречаются
задачи на преобразования матриц за счет изменения значений их элементов. Рассмотрим пример на умножение заданной с клавиатуры строки матрицы на элемент, являющийся "седловой" точкой, т.е. например, минимальным элементом из максимальных элементов по строкам. Для решения такой задачи следует определить значение "седловой" точки. Это можно сделать, организовав поиск максимального элемента по каждой строке и занесение его в элемент соответствующий индексу этой строки одномерного массива. Далее найти минимальный элемент в получившемся массиве, который и будет являться "седловой" точкой. После алгоритм становится достаточно не сложным. Необходимо ввести с клавиатуры индекс строки для преобразования и в цикле по столбцам преобразовать все элементы заданной строки, умножив их значение на полученный элемент "седловой" точки.
Слайд 24
Операции с элементами матриц
Const
n=7;
m=6;
Var
i, j, max, sedlt, t:
integer;
a : array [1..n,1..m] of integer;
b : array
[1..n] of integer;
Begin
randomize;
writeln (‘Сформирована матрица A’);
for i:=1 to n do
begin
for j:=1 to m do
begin
a[ i,j ]:=random(101);
write (a[ i,j ]:6);
end;
writeln;
end;
writeln (‘Введите номер строки матрицы для ее умножения ее на значение 'седловой' точки ‘);
readln(t);
for i:=1 to n do
begin
max:=a[i][1];
for j:=2 to m do
if (a[ i,j ]>max)
max:=a[ i,j ];
b[ i ]:=max;
end;
sedlt:=b[1];
for i:=1 to n do
if (b[ i ] sedlt=b[ i ];
for j:=1 to m do
a[ t,j ]:=a[ t,j ]*sedlt;
printf (‘Получена матрица ‘);
for i:=1 to n do
begin
for j:=1 to m do
write (a[ i,j ]:5);
writeln;
end
End.
Слайд 25
Преобразование матрицы в одномерный массив
Обработка одномерных статических массивов
осуществляется быстрее, чем двумерных того же размера, что часто
требует выполнения указанного преобразования. Требуется переслать элементы матрицы n*m в одномерный массив того же размера по строкам с сохранением порядка следования элементов.
Для этого нужно соответствующим образом согласовать индексы исходной матрицы А и формируемого одномерного массива Х.
Слайд 26
Преобразование матрицы в одномерный массив
Const
n=3;
m=4;
Var
i, j : integer;
a : array [1..n,1..m] of integer;
x : array [1..n*m]
of integer;
Begin
randomize;
writeln (‘Сформирована матрица A’);
for i:=1 to n do
begin
for j:=1 to m do
begin
a[ i,j ]:=random(101);
write (a[ i,j ]:6);
end;
writeln;
end;
for i:=1 to n do
for j:=1 to m do
x[ (i-1)*m+j ]=a[ i,j ];
writeln (‘Получен массив X’);
for i:=1 to n*m do
write (x[ i ]:6);
End.
Слайд 27
Многомерные массивы
Массивы могут быть более чем двумерными.
Пример:
…
a :
array [1..5, 1..3, 1..16, 1..4 ] of real;
…
for i:=1
to 5 do
for j:=1 to 3 do
for k:=1 to 16 do
for m:=1 to 4 do
a[ i,j,k,m ]:=random(101);
…



![Язык Паскаль. Лекция 7 - Двумерные массивы Ввод – вывод элементов двумерного массиваConst n=6; m=8;Var a : array [1..n, 1..m] of integer; I,](/img/tmb/11/1089152/afe4cff9f642ee71d20fe5ebe7de4a7e-720x.jpg)



![Язык Паскаль. Лекция 7 - Двумерные массивы Квадратные матрицыConst n=9;Var a : array [1..n, 1..n] of integer; I, j, s, p :](/img/tmb/11/1089152/88f181816b7d709461d8abc94a5d1111-720x.jpg)
![Язык Паскаль. Лекция 7 - Двумерные массивы Транспонирование матрицConst n=5; m=7;Vari, j : integer; a : array [1..n,1..m] of integer;b :](/img/tmb/11/1089152/d8fd3aa1566cc7c9378116a8cd7b3490-720x.jpg)

![Язык Паскаль. Лекция 7 - Двумерные массивы Транспонирование матрицConst n=9;Vari, j, tmp : integer; a : array [1..n,1..n] of integer;Beginrandomize;writeln](/img/tmb/11/1089152/e32ba5351de760d2506ab7f4ae8c1e1c-720x.jpg)

![Язык Паскаль. Лекция 7 - Двумерные массивы Умножение матрицы на векторConst n=6; m=9;Vari, j, s : integer; a : array [1..n,1..m]](/img/tmb/11/1089152/525bde2001fde7e73621ea4cf81d7ca8-720x.jpg)

![Язык Паскаль. Лекция 7 - Двумерные массивы Умножение матрицы на матрицу write (a[ i,j ]:6); end; writeln();end;for i:=1 to n do for j:=1](/img/tmb/11/1089152/0304da402cdf19278c404d8d5646f40e-720x.jpg)







![Язык Паскаль. Лекция 7 - Двумерные массивы Преобразование матрицы в одномерный массивConst n=3; m=4; Vari, j : integer; a : array [1..n,1..m]](/img/tmb/11/1089152/7b7a85a875336dd87d15a37688755da7-720x.jpg)