- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку Решение задач по теме Объемы тел
Содержание
- 2. Свойства объема Каждое тело имеет
- 3. Объем призмыОбъем любого цилиндра можно найти по
- 4. Объем пирамидыОбъем пирамиды вычисляется по формуле:
- 5. Объем тела
- 6. Объем конуса. Теорема. Объем конуса равен одной трети произведения площади основания на высоту.
- 7. Объем шараОбъем шара вычисляется по формуле: , где R – радиус шара.
- 11. № 27118. Одна цилиндрическая кружка вдвое выше
- 12. № 27091 В цилиндрический сосуд, в котором
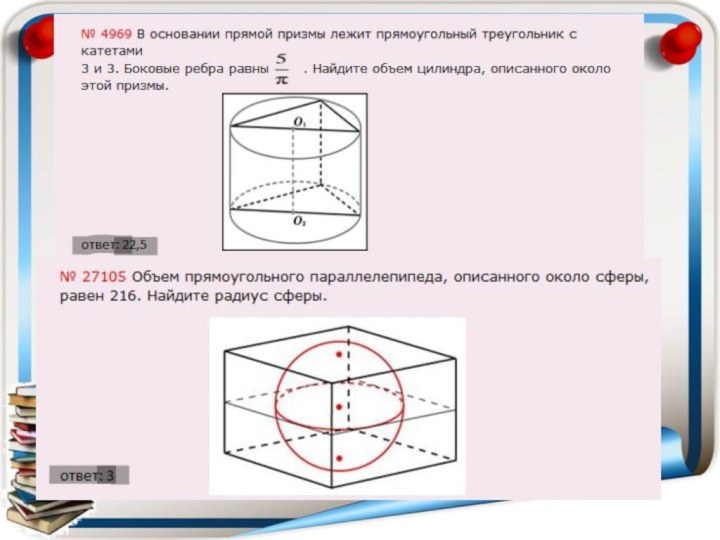
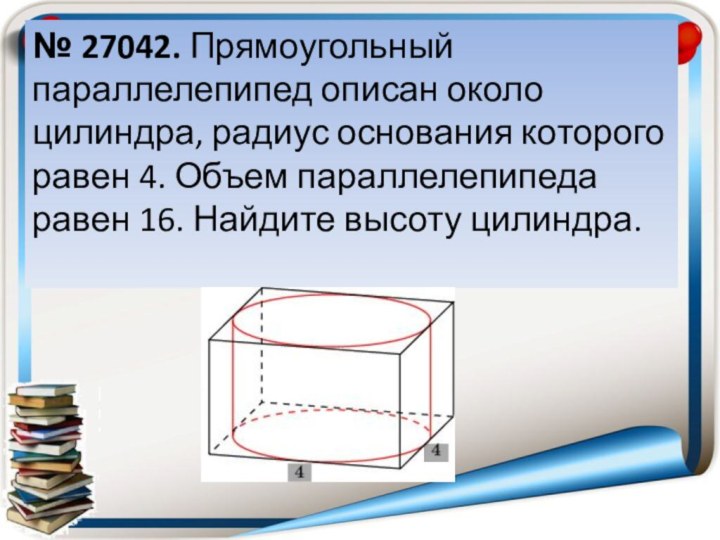
- 13. № 27042. Прямоугольный параллелепипед описан около цилиндра,
- 14. № 27065. Найдите площадь боковой поверхности правильной
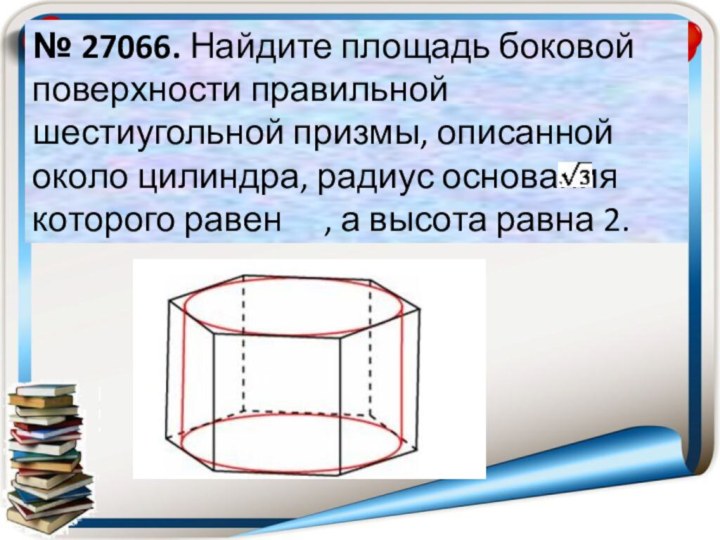
- 15. № 27066. Найдите площадь боковой поверхности правильной
- 16. № 27046. В цилиндрическом сосуде уровень жидкости
- 17. Скачать презентацию
- 18. Похожие презентации
Свойства объема Каждое тело имеет определенный объем, выраженный положительным числом.Равные тела имеют равные объемы. Если тело разбито на несколько частей, то его объем равен сумме объемов всех его частей.












Слайд 2
Свойства объема
Каждое тело имеет определенный
объем, выраженный положительным числом.
тело разбито на несколько частей, то его объем равен сумме объемов всех его частей.
Слайд 3
Объем призмы
Объем любого цилиндра можно найти по формуле:
, где S
– площадь основания, h – высотаДоказательство:
1 СЛУЧАЙ:
Для произвольной треугольной призмы ABDA1B1D1. Рассмотрим в пространстве точки С и С1 такие, что ABCD— параллелограмм, а СС1=АА1 иСС1//АА1. Тогда получим параллелепипед ABCDA1B1C1D1 который диагональным сечениемBB1D1D разбивается на две призмы ABDA1B1D1и BCDB1С1D1 (рис. 43, а). Эти призмы равны (если совместить их равные основания ABD и CDB и равные ребра АА1 и СС1, тогда призмы совместятся), следовательно, равны их объемы. Таким образом, объем построенного параллелепипеда равен удвоенному объему данной призмы. Объем Vo параллелепипеда равен произведению площади основания на высоту. Площадь основания параллелепипеда равна удвоенной площади треугольника ABD, а его высота равна высоте h данной призмы. Следовательно, объем данной призмы равен произведению площади ее основания на высоту:
Слайд 4
Объем пирамиды
Объем пирамиды вычисляется по формуле:
где S –
площадь основания, H – высота пирамиды.
Доказательство:
1 СЛУЧАЙ
Дополним треугольную пирамиду PABC до треугольной призмы ABCPED,
у которой такие же высота и основание. Эта призма состоитиз трех пирамид: PABC, PBDE и PBCD. Докажем, что их объемы равны.
У пирамид PABC и PBDE равные высоты и равновеликие основания.
Согласно лемме эти пирамиды имеют равные объемы. У пирамид PBCD
и PBDE общая высота и равновеликие основания, так как Δ BCD = Δ BDE.
Таким образом, объем пирамиды PABC втрое меньше объема призмы ABCPED:
что и требовалось доказать.
ОГЛАВЛЕНИЕ
Слайд 6
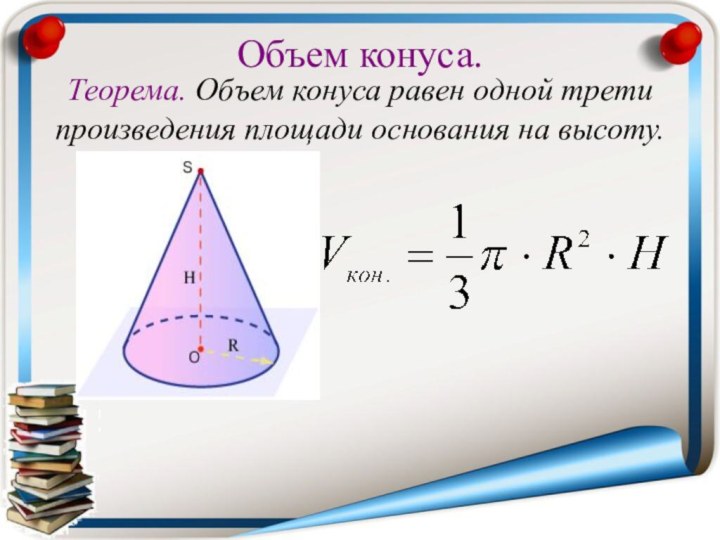
Объем конуса.
Теорема. Объем конуса равен одной трети
произведения площади основания на высоту.
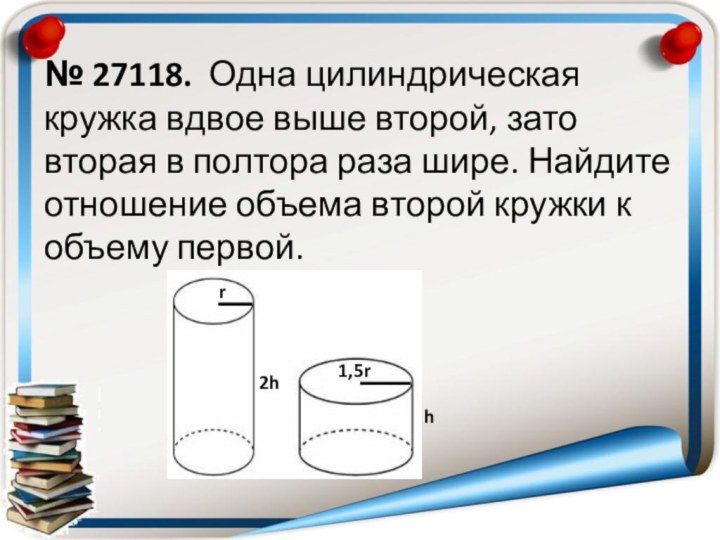
Слайд 11 № 27118. Одна цилиндрическая кружка вдвое выше второй,
зато вторая в полтора раза шире. Найдите отношение объема
второй кружки к объему первой.2h
h
r
1,5r
Слайд 12 № 27091 В цилиндрический сосуд, в котором находится
6 дм3 воды, опущена деталь. При этом уровень жидкости
в сосуде поднялся в 1,5 раза. Чему равен объем детали?Слайд 13 № 27042. Прямоугольный параллелепипед описан около цилиндра, радиус
основания которого равен 4. Объем параллелепипеда равен 16. Найдите
высоту цилиндра.Ответ: 32
Слайд 14 № 27065. Найдите площадь боковой поверхности правильной треугольной
призмы, описанной около цилиндра, радиус основания которого равен
, а высота равна 2.Слайд 15 № 27066. Найдите площадь боковой поверхности правильной шестиугольной
призмы, описанной около цилиндра, радиус основания которого равен
, а высота равна 2.Слайд 16 № 27046. В цилиндрическом сосуде уровень жидкости достигает
16 см. На какой высоте будет находиться уровень жидкости,
если ее перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.





























