Презентация на тему по математике (тригонометрия)

и вычитания аргументов
5.Числовая окружность
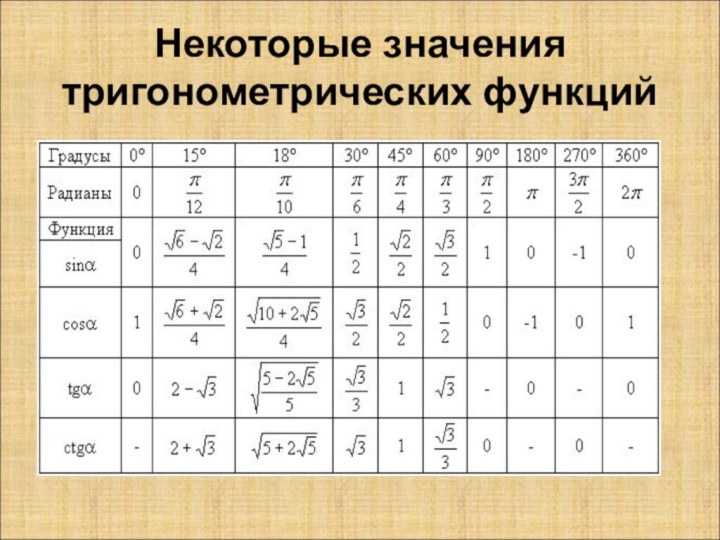
6.Некоторые значения тригонометрических функций
7.Четность тригонометрических функций
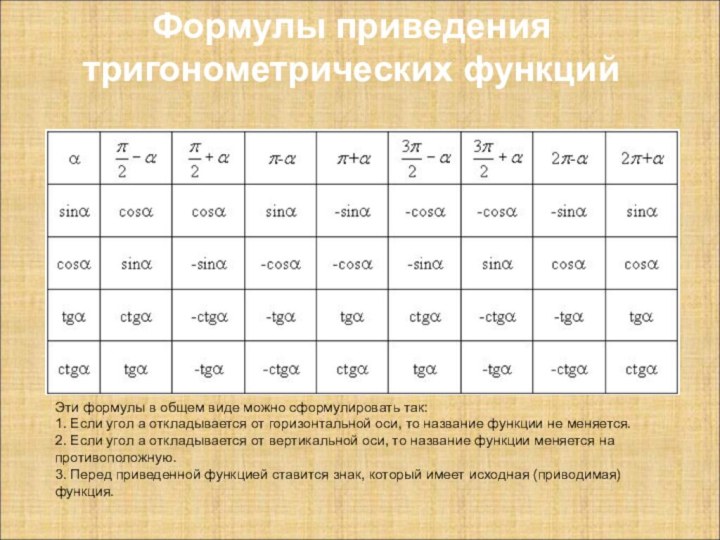
8.Формулы

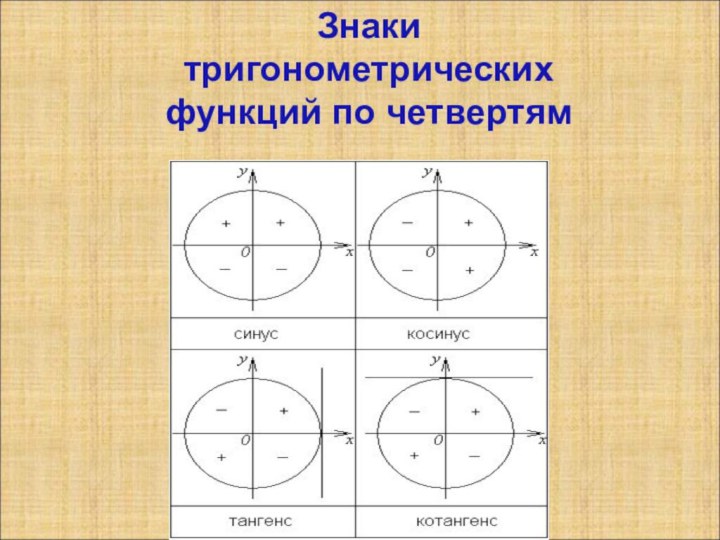
приведения
9.Знаки тригонометрических функций по четвертям

Содержание

Истоки тригонометрии берут начало в древнем Египте, Вавилонии и

долине Инда более 3000 лет назад. Индийские математики были первопроходцами в применении алгебры и тригонометрии к астрономическим вычислениям. Лагадха — единственный из самых древних известный сегодня математик, использовавший геометрию и тригонометрию в своей книге «Джьётиша-веданга» («Jyotisa Vedanga»), бо́льшая часть работ которого была уничтожена иностранными захватчиками.
Греческий математик Клавдий Птолемей также внес большой вклад в развитие тригонометрии. Значительный вклад в развитие тригонометрии внесли арабские ученые Аль-Батани (850-929) и Абу-ль-Вафа, Мухамед-бен Мухамед (940-998), который составил таблицы синусов и тангенсов через 10’ с точностью до 1/604. Теорему синусов уже знали индийский ученый Бхаскара (р. 1114, год смерти неизвестен) и азербайджанский  астроном и математик Насиреддин Туси Мухамед (1201-1274). Кроме того, Насиреддин Туси в своей работе «Трактат о полном четырехстороннике» изложил плоскую и сферическую тригонометрию как самостоятельную дисциплину.

История

новая математическая модель – числовая окружность.
Пример 1. Дана окружность

радиусом 1см. Чему равна длина окружности, ее половины, ее четверти?
Решение. Длина L окружности радиусом R вычисляется по формуле: L=2πR, где π≈3,14.
Если R =1см, то
L=2 π см ≈6,28см.
Длинна половины окружности равна π см, а длинна четверти окружности (AB, BC, CD или DA) равна π/2 см.
Ответ: ≈6,28 см; ≈3,14 см; ≈1,57.

Введение

sinαcosβ + cosαsinβ
2.sin(α – β) = sinαcosβ –

cosαsinβ
3.cos(α – β) = cosαcosβ + sinαsinβ
4.cos(α + β) = cosαcosβ – sinαsinβ

5.

6.

7.

8.

действительными числами и точками окружности) будем называть числовой окружностью.
Пример

1. Найти на числовой окружности точку, которая соответствует заданному числу: π/2, π, 3π/2.
Решение: Так как все числа положительны, то для отыскания соответствующих им точек окружности нужно пройти по окружности путь заданной длины, двигаясь из точки А в положительном направлении. Учтем при этом, что длина каждой четверти единичной окружности равна π/2.
АВ=π/2, значит, числу π/2 соответствует точка В; В=В(π/2).

четная, поэтому cos(-a)=cosa Функции tga и ctga нечетные, поэтому tg(-a)=-tga

и ctg(-a)=-ctga

Четность тригонометрических функций

Если угол a откладывается от горизонтальной оси, то название

функции не меняется. 2. Если угол a откладывается от вертикальной оси, то название функции меняется на противоположную. 3. Перед приведенной функцией ставится знак, который имеет исходная (приводимая) функция.

Формулы приведения тригонометрических функций