- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Презентации по математике учащихся
Содержание
- 2. ОпределениеПравильным называется многогранник, у которого все грани
- 3. Существует 5 типов правильных многогранниковПравильный додекаэдрПравильный икосаэдрПравильный гексаэдрПравильный тетраэдрПравильный октаэдр
- 4. Многоугольники, из которых составлен многогранник, называются гранями.Стороны
- 5. В каждой вершине многогранника должно сходиться столько
- 6. спередислеваснизусверхусзадисправаПравильный многогранник, у которого грани правильные треугольники
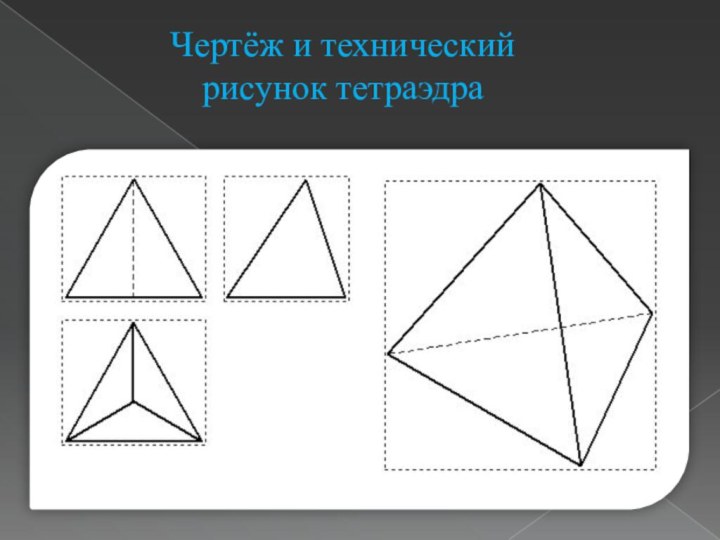
- 7. Чертёж и технический рисунок тетраэдра
- 8. спередисправаслевасверхусзадиснизуПравильный многогранник, у которого грани – квадраты
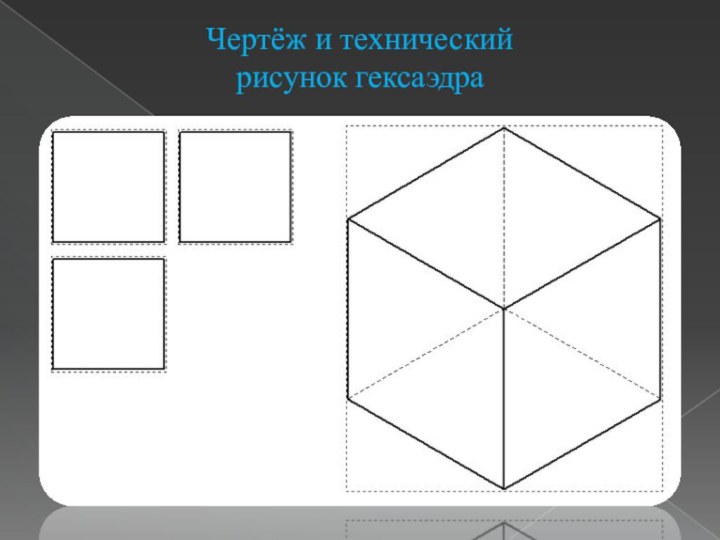
- 9. Чертёж и технический рисунок гексаэдра
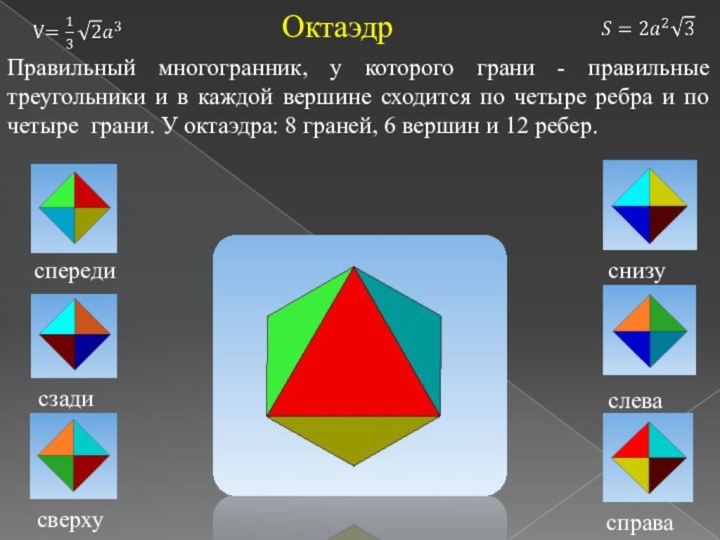
- 10. спередисзадисверхусправаслеваснизуОктаэдрПравильный многогранник, у которого грани - правильные
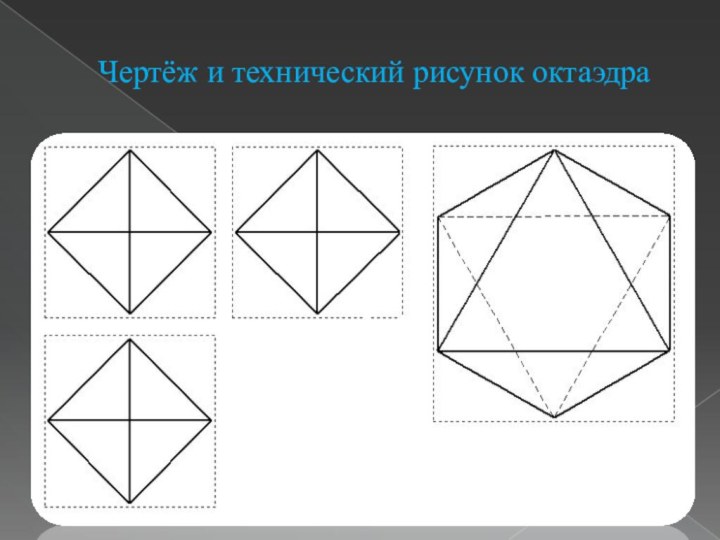
- 11. Чертёж и технический рисунок октаэдра
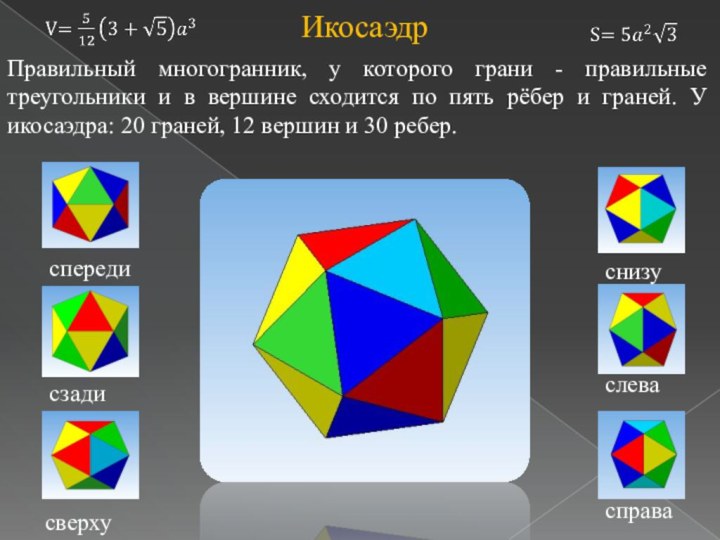
- 12. справаслеваснизуспередисзадисверхуПравильный многогранник, у которого грани - правильные
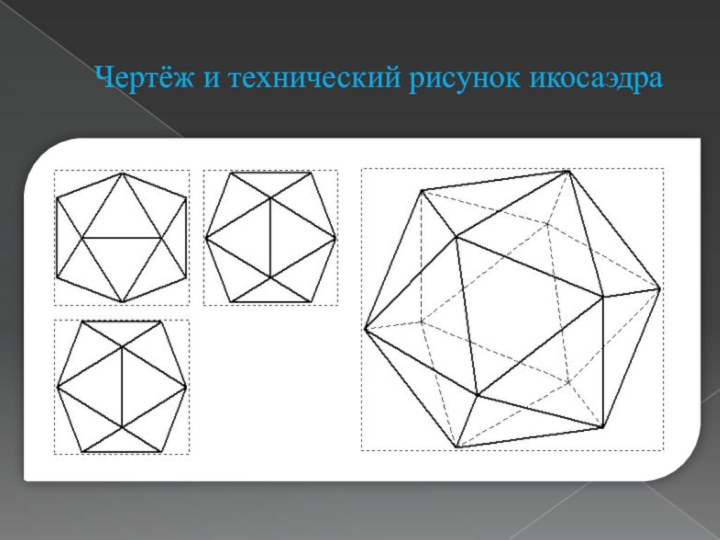
- 13. Чертёж и технический рисунок икосаэдра
- 14. спередисзадисверхусправаслеваснизуПравильный многогранник, у которого грани правильные пятиугольники
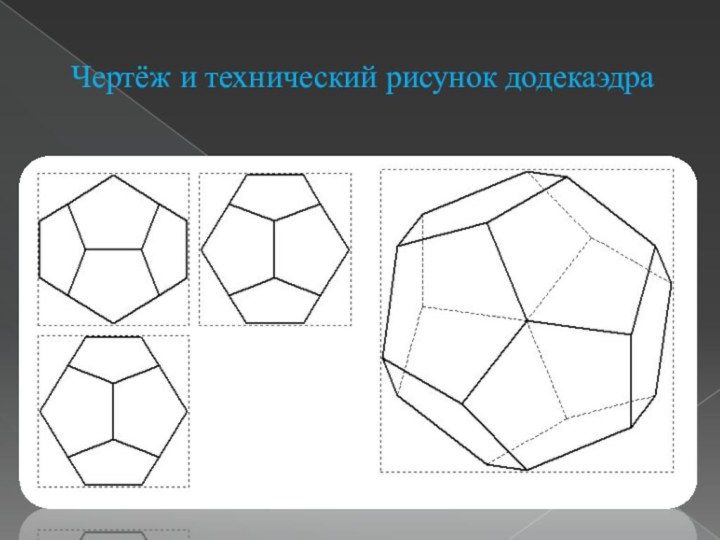
- 15. Чертёж и технический рисунок додекаэдра
- 16. Историческая справка О существовании всего лишь пяти
- 17. Применение в кристаллографии Тела Платона нашли широкое
- 18. Поваренная соль состоит из кристаллов в форме
- 19. В набор "Юный геометр" входит несколько плоских
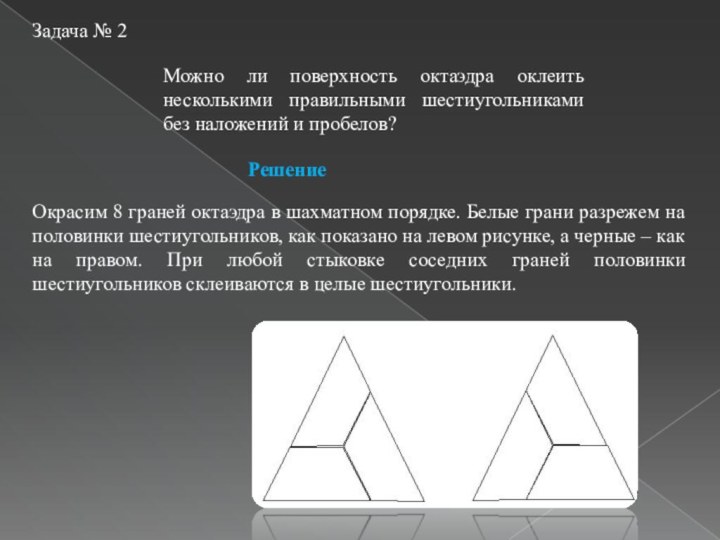
- 20. Задача № 2Можно ли поверхность октаэдра оклеить
- 21. Скачать презентацию
- 22. Похожие презентации











Слайд 2
Определение
Правильным называется многогранник, у которого все грани являются
правильными многоугольниками, и все многогранные углы при вершинах равны.
– это часть пространства, ограниченная совокупностью конечного числа плоских многоугольников, соединённых таким образом, что каждая сторона любого многогранника является стороной ровно одного многоугольника. Многоугольники называются гранями, их стороны – рёбрами, а вершины – вершинами.
Слайд 3
Существует 5 типов правильных многогранников
Правильный додекаэдр
Правильный икосаэдр
Правильный гексаэдр
Правильный
тетраэдр
Правильный октаэдр
Слайд 4
Многоугольники, из которых составлен многогранник, называются гранями.
Стороны граней
называются рёбрами.
А концы рёбер называют вершинами многоугольника.
Гранью куба является
квадратА
В
АВ является ребром куба
А
А является вершиной куба
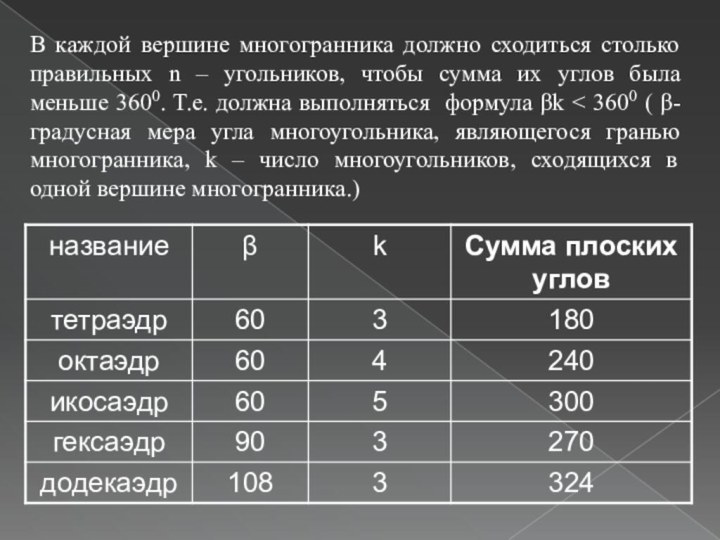
Слайд 5 В каждой вершине многогранника должно сходиться столько правильных
n – угольников, чтобы сумма их углов была меньше
3600. Т.е. должна выполняться формула βk < 3600 ( β-градусная мера угла многоугольника, являющегося гранью многогранника, k – число многоугольников, сходящихся в одной вершине многогранника.)
Слайд 6
спереди
слева
снизу
сверху
сзади
справа
Правильный многогранник, у которого грани правильные треугольники и
в каждой вершине сходится по три ребра и по
три грани. У тетраэдра: 4 грани, четыре вершины и 6 ребер.Тетраэдр
Слайд 8
спереди
справа
слева
сверху
сзади
снизу
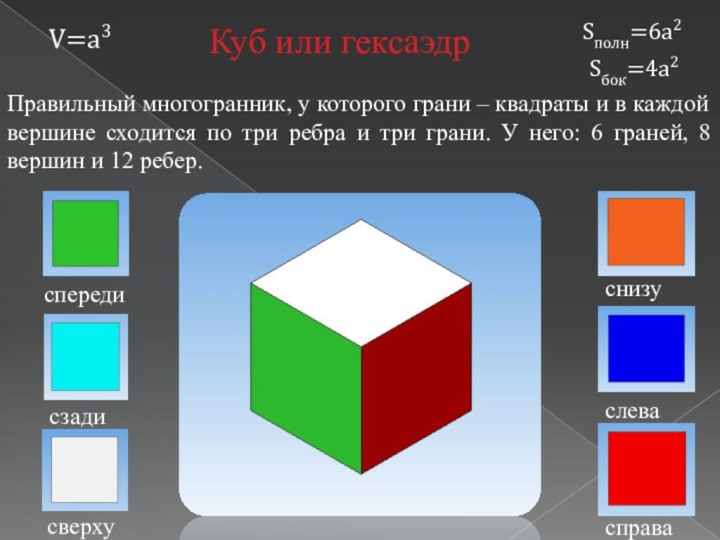
Правильный многогранник, у которого грани – квадраты и
в каждой вершине сходится по три ребра и три
грани. У него: 6 граней, 8 вершин и 12 ребер.Куб или гексаэдр
V=a3
Sполн=6a2
Sбок=4a2
Слайд 10
спереди
сзади
сверху
справа
слева
снизу
Октаэдр
Правильный многогранник, у которого грани - правильные треугольники
и в каждой вершине сходится по четыре ребра и
по четыре грани. У октаэдра: 8 граней, 6 вершин и 12 ребер.
Слайд 12
справа
слева
снизу
спереди
сзади
сверху
Правильный многогранник, у которого грани - правильные треугольники
и в вершине сходится по пять рёбер и граней.
У икосаэдра: 20 граней, 12 вершин и 30 ребер.Икосаэдр
Слайд 14
спереди
сзади
сверху
справа
слева
снизу
Правильный многогранник, у которого грани правильные пятиугольники и
в каждой вершине сходится по три ребра и три
грани. У додекаэдра:12 граней, 20 вершин и 30 ребер.Додекаэдр
Слайд 16
Историческая справка
О существовании всего лишь пяти правильных
многогранников знали еще в Древней Греции. Великий древнегреческий мыслитель
Платон считал, что четыре из них олицетворяют четыре «стихии»: тетраэдр – огонь, куб – землю, икосаэдр – воду, октаэдр – воздух. Пятый же многогранник, додекаэдр, символизировал собой все мироздание, представлял собой образ всей Вселенной, почитался главнейшим и его стали называть quinta essentia (квинта эссенциа) или «пятая сущность».Правильные многогранники называют иногда Платоновыми телами, им посвящена последняя книга «Начал» Евклида. Её считают венцом стереометрии у древних греков.
Слайд 17
Применение в кристаллографии
Тела Платона нашли широкое применение
в кристаллографии, так как многие кристаллы имеют форму правильных
многогранников.Например, куб - монокристалл поваренной соли (NaCl), октаэдр - монокристалл алюмокалиевых квасцов, одна из форм кристаллов алмаза – октаэдр.
Кристаллы бывают самой различной формы: 1 — берилл, 2 — аметист, 3 — рубин, 4 — кристалл металла германия — денорит, 5 — горный хрусталь, 6 — испанский шпат, 7 — поваренная соль, 8 — ограненный алмаз—бриллиант, вправленный в кольцо.
В колбе с перенасыщенным раствором на конце проволочки, опущенной в раствор, растет кристалл поваренной соли.
Слайд 18 Поваренная соль состоит из кристаллов в форме куба
Минерал сильвин также имеет кристаллическую решетку в форме куба.
Молекулы воды имеют форму тетраэдра.
Минерал куприт образует кристаллы в форме октаэдров.
Скелет одноклеточного организма феодарии представляет собой икосаэдр.
Кристаллы пирита имеют форму додекаэдра.
Слайд 19 В набор "Юный геометр" входит несколько плоских граней,
из которых можно собрать выпуклый многогранник. Юный геометр Семён
разделил эти грани на две кучки. Могло ли случиться, что из граней каждой кучки тоже можно собрать выпуклый многогранник? (И в начале, и в конце каждая из граней набора должна являться гранью многогранника.)Например, из граней правильного октаэдра можно сложить два правильных тетраэдра.
Решение
Задача №1





























